Sod's shock tube (1D - Hydro - Cartesian)
This problem is initiated by a left region of high density and pressure and a right region of low density and pressure. The gas is initially at rest everywhere. The discontinuity creates a shock wave which propagates towards the right and a rarefaction wave propagating towards the left. The two waves are separated by a contact discontinuity. This test is the basic standard test every hydro code should pass.
Set up
Domain: -0.5 ≤ x ≤ 0.5
Boundary conditions: Free flow everywhere
Equation of state: Adiabatic with γ = 7/5
Initial density: ρ = 1.0 for x ≤ 0.0 and ρ = 0.125 for x > 0.0
Initial pressure: p = 1.0 for x ≤ 0.0 and p = 0.1 for x > 0.0
Initial velocity: Zero everywhere
Grid resolution: nx = 100
|
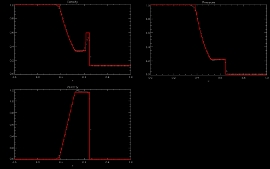
Sod shock tube at time t = 0.1 s |
Sedov blastwave (1D - Hydro - Spherical)
This problem is initiated by an overpressured region in the center of the domain. The result is a strong outward moving spherical shock with rarified fluid inside the sphere.
Set up
Domain: 0.0 ≤ r ≤ 2.0
Boundary conditions: Reflecting at r = 0 and free flow at r = 2.0
Equation of state: Adiabatic with γ = 7/5
Initial density: ρ = 1.0 everywhere
Initial pressure: p = 1.6 × 106 for r ≤ 4 × 10-3 and p = 1.6 × 10-6 otherwise
Initial velocity: Zero everywhere
Grid resolution: nx = 512
|
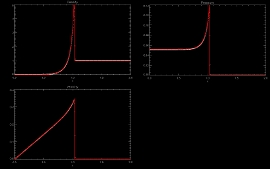
Sedov blastwave at time t = 1.0 s
|
Hydrodynamical implosion (2D - Hydro - Cartesian)
This problem is initiated by an overpressured region above the line x+y = 0.5. This overpressure sends a shock wave towards the origin. The shock hits the reflecting boundaries at x=0 and y=0, and the resulting reflections create jets that eventually interact with each other at the origin. This interaction then results in the production of another jet along the diagonal, x=y. This jet interacts with the shocks that are being reflected back and forth in the box.
This problem is very good at testing the algorithm's ability to maintain symmetry. Throughout the evolution, the fluid must be symmetric across x=y. If this symmetry is not exactly maintained, there will be no jet along x=y. Furthermore, the less numerical diffusion there is, the longer and narrower this jet will be.
Set up
Domain: 0.0 ≤ x ≤ 1.0, 0.0 ≤ y &le 1.0
Boundary conditions: Reflecting everywhere
Equation of state: Adiabatic with γ = 7/5
Initial density: &rho = 1.0 for x+y > 0.5 and ρ = 0.125 for x+y ≤ 0.5
Initial pressure: p = 1.0 for x+y > 0.5 and p = 0.4 for x+y ≤ 0.5
Initial velocity: Zero everywhere
Grid resolution: nx = 500, ny = 500
|

Hydrodynamical implosion at time t = 5.0 s
|
MHD shock tube (1D - MHD - Cartesian)
This problem is initiated by a left region of high density and pressure and a right region of low density and pressure. The gas is initially at rest everywhere. The discontinuity creates a shock wave which propagates towards the right and a rarefaction wave propagating towards the left. The two waves are separated by a contact discontinuity.
Set up
Domain: -1.0 ≤ x ≤ 1.5
Boundary conditions: Free flow everywhere
Equation of state: Adiabatic with γ = 5/3
Initial density: ρ = 1.0 for x ≤ 0.0 and ρ = 0.2 for x > 0.0
Initial pressure: p = 1.0 for x ≤ 0.0 and p = 0.2 for x > 0.0
Initial velocity: Zero everywhere
Initial magnetic field: Bx = 1.0
Grid resolution: nx = 800
|
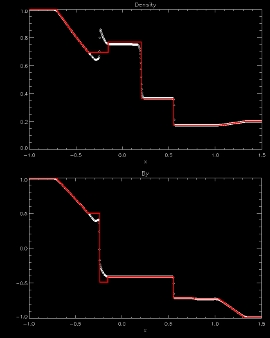
MHD shock tube at time t = 0.4 s
|
Orszag-Tang vortex (2D - MHD - Cartesian)
The Orszag-Tang Vortex is a well-known test for MHD codes. The intial conditions lead to a system of supersonic MHD turbulence, making this problem a good test of the algorithm's ability to handle such turbulence and MHD shocks. Furthermore, given the set up described here, the problem is symmetric under a rotation of 180°, providing a symmetry test for the MHD version of the algorithm.
Set up
Domain: 0.0 ≤ x ≤ 1.0, 0.0 ≤ y ≤ 1.0
Boundary conditions: Periodic everywhere
Equation of state: Adiabatic with γ = 5/3
Initial density: ρ = 4π everywhere
Initial pressure: p = γ/4π everywhere
Initial velocity: vx = -sin(2πy), vy = sin(2πx)
Initial magnetic field: Bx = - B0 sin(2πy), By = B0 sin(4πx)
Grid resolution: nx = 128, ny = 128
|

Orszag-Tang vortex at time t = 0.51 s
|
Marshak wave (1D - Radiative transfer - Cartesian)
This problem is initiated by a radiative energy entering the computational domain from the left and being absorbed by the gas. As the gas heats up, it re-radiates some energy in the forward direction which heats the gas ahead and generates a propagating Marshak wave.
Set up
Domain: 0.0 ≤ x ≤ 12.0
Boundary conditions: Left: Tr = 1000 K, Right: Tr = 300 K
Equation of state: γ = 5/3, μ = 1.25 × 108
Initial density: ρ = 1.0 × 10-3 everywhere
Initial temperature: T = 300 K everywhere, Tr = 300 K everywhere
Initial velocity: Zero everywhere
Grid resolution: nx = 200
|
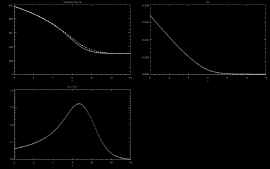
Marshak wave at time t = 1.36 × 10-7 s
|
Subcritical radiative shock (1D - RHD - Cartesian)
This problem is initiated by the gas in the domain moving at a high speed towards the left and hitting the left reflecting boundary condition. The reflecting wall generates the propagation of a shock wave with a radiative precursor towards the right.
Set up
Domain: 0.0 ≤ x ≤ 7 × 1010
Boundary conditions: Left: reflexive, Right: free flow
Equation of state: γ = 7/5, μ = 1.0
Initial density: ρ = 7.78 × 10-10 everywhere
Initial temperature: T = 10 K everywhere, Tr = 10 K everywhere
Initial velocity: -6.0 km/s everywhere
Grid resolution: nx = 300
|
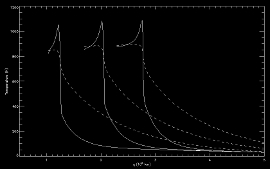
Sub-critical radiative shock at times t = 1.7 × 104 s, 2.8 × 104 and 3.8 × 104 s
|
Supercritical radiative shock (1D - RHD - Cartesian)
This problem is initiated by the gas in the domain moving at a high speed towards the left and hitting the left reflecting boundary condition. The reflecting wall generates the propagation of a shock wave with a radiative precursor towards the right.
Set up
Domain: 0.0 ≤ x ≤ 7 × 1010
Boundary conditions: Left: reflexive, Right: free flow
Equation of state: γ = 7/5, μ = 1.0
Initial density: ρ = 7.78 × 10-10 everywhere
Initial temperature: T = 10 K everywhere, Tr = 10 K everywhere
Initial velocity: -20.0 km/s everywhere
Grid resolution: nx = 300
|
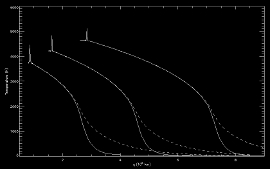
Super-critical radiative shock at times t = 4.0 × 103 s, 7.5 × 103 and 1.3 × 104 s
|
Rayleigh-Taylor instability (2D - Hydro + Gravity - Cartesian)
This instability results from perturbing a fluid of high density resting on top of a low-density fluid where the gravitational acceleration is downward. This problem tests the implementation of the gravity source term to the fluid equations.
Set up
Domain: -0.25 ≤ x ≤ 0.25. -0.75 ≤ y ≤ 0.75
Boundary conditions: Periodic in x, Reflexive in y
Equation of state: Adiabatic with γ = 7/5
Initial density: ρ = 1.0 for y ≤ 0.0 and ρ = 2.0 for y ≥ 0.0
Initial pressure: The pressure is initialized to give hydrostatic equilibrium: p = 2.5 ρgy everywhere
Initial velocity: The x velocity is zero everywhere. The y velocity is perturbed with a single mode perturbation with A [1+cos(2πx/Lx)] [1+cos(2πy/Ly)]/4 with Lx and Ly being the size of the x and y domains respectively, and A = 0.01.
Grid resolution: nx = 200, ny = 600
|

Rayleigh-Taylor instability at time t = 12.4 s. Left: minmod slope limiter; Right: positivity preserving.
|