The series of Jefferson Laboratory (USA) experiments dedicated to the measurement of electron-proton elastic scattering showed that the extracted information on the proton structure did not agree when extracted from two kinds of experiments. To reconcile these results, it was suggested that, beyond the exchange of one photon, that is the dominant mechanism, the exchange of a second photon could become important. The presence of a second photon would bring serious consequences, casting doubts on the results of number of experiences. That’s why the search of such mechanism motivated three independent experiments, recently realized. We have analyzed all the obtained results and shown that two photon exchange is not enhanced. Other explanations are favored, as a precise calculation of radiative corrections. This study, performed by two researchers of IRFU and JINR-BLTP, Dubna (Russia) has been published in the Physical Review C[1].
Elastic electron-proton scattering is a reaction where the initial and final states are the same (an electron and a proton). Two experimental methods have been currently applied, in order to learn about the proton structure using this reaction:
The underlying theory is the same for the two methods and assumes that the interaction occurs through the exchange of a virtual photon, i.e., a massive photon whose mass coincides with the four-momentum transfer squared (Q2 = -q2) (Fig. 1). These experiments allow one to extract the ‘electric and magnetic form factors’, quantities that parametrize the spatial distribution of the electric and magnetic charge inside the proton.
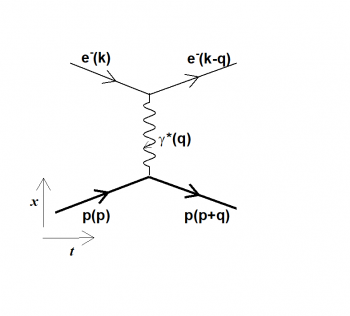
Fig. 1: Feynman diagram representing elastic electron (e-)-proton (p) scattering. The reaction takes place in four dimensions: the time (horizontal axis) et the space (vertical axis). The proton is unchanged after receiving and sharing among its constituents a momentum q transferred through a virtual photon (?*) emitted by the incident electron.
The electric and magnetic form factors extracted from the ‘Rosenbluth’ data made consensus, as, on one side, they follow the large Q² behavior predicted by quantum chromodynamics, the theory of the strong interaction, and, on the other side, they suggest an exponential charge density distribution, consistent with semi-classical models. A.I. Akhiezer et M.P. Rekalo suggested in the 1970’s another method, which could be only recently applied, since it requires high intensity, polarized electron accelerators, as well as polarimeters that will measure the polarization of the recoiling proton. It turns out that the form factors ratio measured following this method, not only is more precise, as expected, but deviates essentially from the one given by the ‘Rosenbluth’ method. It appears that, contrary to what previously accepted, the electric and magnetic charge distributions in the proton are different. This difference is attributed mainly to the electric form factor, as the precision on the magnetic term by the ‘Rosenbluth’ method is good.
Is there a second photon exchanged?
To reconcile these results, it was suggested that the exchange of a second photon may occur during the interaction. Experimental and theoretical studies of these effects were undertaken since the 70’s, with no clear experimental evidence. In case of two photon exchange, the extraction of the information on the proton structure in terms of form factors, is very complicated and may depend on underlying models. Indeed, the calculations are model dependent and rely on assumptions poorly constrained by the data. However, it is possible to predict some consequences of the presence of two photons during the interaction, in model independent way. In particular, the elastic electron-proton scattering cross section (e-p) has to be different from the elastic positron (the antiparticle of the electron)-proton scattering cross section (e+p) [2]. This follows from the fact that, in presence of two photon exchange, new contributions arise, that depend on the beam charge (electrons or positrons). The ratio of cross sections for elastic scattering (e+p/e-p) in the same kinematical conditions will differ from unity.
Three experiments: VEPP, OLYMPUS and CLAS
Even if the emission of an additional photon is suppressed by a factor one hundred (the emission of each photon is proportional to the fine electromagnetic constant α, α≈ 1/137), some models predicted a relative probability of two photon exchange as large as 10%. Three experiments were built to measure the elastic cross-section ratio (e+p/e-p) with positron and electron beams: VEPP at Novosibirsk (Russia) [3], OLYMPUS at DESY (Germany) [4], CLAS at Jefferson Laboratory (USA) [5]. The techniques and the associated errors being very different, their results published in 2015 and 2017, have to be considered independent.
Before this series of experiments, we had already determined an upper limit of the two photons exchange contribution in electron-proton elastic scattering by calculating elastic electron-muon scattering [6] (the muon is a massive, structureless elementary particle, of the same family of the electron but about 200 times heavier). More recently, we have shown the importance of taking precisely into account radiative corrections in electron-proton elastic scattering [7]. These corrections consist in taking into account the energy loss, by photon emission, of all the charged particles participating in the reaction. This radiation modifies the particle kinematics before and after the interaction. We have shown that the largest discrepancy between the elastic cross sections for (e+p) and (e-p), i.e., the charge asymmetry, is due to the interference between the photon emission in the initial and final states [8]. With the knowledge acquired in our previous studies, we have reinterpreted all the results of the recent experiments in the light of our calculation of charge asymmetry [1]. Figure 2 shows the difference between our calculation and the data of the three experiments, for the ratio between the cross section for the elastic scattering of positrons and of electrons, after applying radiative corrections.
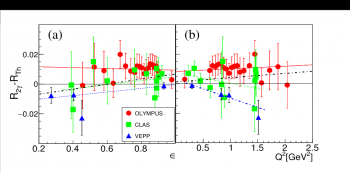
Fig. 2: Difference between the ratio R, theoretical (RTh) and experimental (R2?), that quantifies the charge asymmetry for the data of the three experiments: VEPP (blue triangles), OLYMPUS (red circles) and CLAS (green squares). This ratio is plotted as a function of the parameter ?, related to the electron scattering angle and of the transferred momentum, Q². A deviation from zero would be the proof of an enhanced contribution of two photon exchange. The figure is taken from Ref. [1].
This difference is compatible with zero for most of the points, which all lie within an interval of ±0.02. The experimental data agree with our model as no deviation beyond 2% is visible. Few percent is the level of precision of the data and calculation: it corresponds to the intrinsic precision of the applied first order radiative corrections (of the order of α, as well as to the precision of the experimental results. Moreover, the data do not show any evident correlation with the chosen kinematical variables (ε, related to the electron scattering angle, and Q², the transferred momentum). The possibility of such correlation had suggested various hypothesis, principally a possible two photon exchange. Our results have been published in Physical Review C, and the paper is in free access under SCOAP3 [1].
Our work shows that it is very unlikely that two photon exchange is responsible of the disagreement between the polarized and non-polarized form factor measurements. The importance of radiative corrections had previously been pointed out by our group [7], and by researchers from Novosibirk [9] few years ago. Our recent work favors the necessity of implementing precise radiative corrections as alternative explanation to an enhanced effect of the two photons exchange mechanism. This conclusion emphasizes the necessity of precise form factor measurements and clarifies the role of the reaction mechanism in the existing data.
1. The spin is a quantum property of a particle. It is assimilated to the direction around which the proton self-rotates. For an electron (or a proton), the spin can take only two values, +1/2 or -1/2. In a vertical direction, the electron (or proton) is then oriented (polarized) up or down.
References:
[1] V. V. Bytev, and E. Tomasi-Gustafsson, Phys. Rev. C99, 025205 (2019).
[2] M. P. Rekalo and E. Tomasi-Gustafsson, Eur. Phys. J. A22, 331 (2004).
[3] I. A. Rachek, et al., Phys. Rev. Lett. 114, 062005 (2015).
[4] B. S. Henderson et al., (OLYMPUS Collaboration), Phys. Rev. Lett. 118, 092501 (2017).
[5] D. Rimal et al., (CLAS Collaboration), Phys. Rev. C 95, 065201 (2017).
[6] E. A. Kuraev and E. Tomasi-Gustafsson, Phys. Part. Nucl. Lett. 7, 67 (2010).
[7] E. A. Kuraev, Yu. M. Bystriskiy, A. I. Ahmadov and E. Tomasi-Gustafsson , Phys. Rev. C89, 065207 (2014).
[8] E. A. Kuraev, V. V. Bytev, S. Bakmaev and E. Tomasi-Gustafsson, Phys.Rev. C78, 015205 (2008).
[9] A. V. Gramolin, et al., J. Phys. G41, 115001 (2014).
Contact : Egle Tomasi-Gustafsson (IRFU/DPhN)
• Structure of nuclear matter › Quarks and gluons hadron structure
• Institute of Research into the Fundamental Laws of the Universe • The Nuclear Physics Division
• Nucleon Structure Laboratory (LSN) - The internal structure of hadrons
