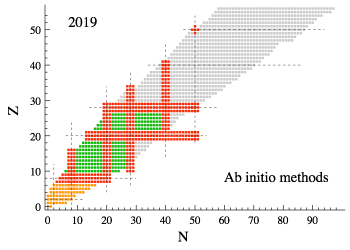
Figure 1: Reach of ab initio methods: quasi-exact methods (orange), valence-space methods (green) and wave-function expansion methods (red).
The predictions of nuclear properties based on a realistic description of the strong interaction is at the heart of the ab initio endeavour in low-energy nuclear theory. Ab initio calculations have long been limited to light nuclei or to nuclei with specific proton and neutron numbers. Theoreticians from Irfu/DPhN have developed novel ab initio methods that led to a significantly increase of the number of nuclei that can be accessed. The most recent one, called Bogoliubov many-body perturbation theory (BMBPT), provides a light-weighted alternative capable of providing the same accuracy as competing methods at a computational cost that is lowered by two orders of magnitude. This has been achieved by allowing symmetries of the nuclear Hamiltonian to spontaneously break in the calculation. This exciting new development, paving the way for precise computations of heavier nuclei using reasonable computing resources, has recently been published in Physics Letter B [1].
Atomic nuclei are systems composed of nucleons, i.e. protons and neutrons, interacting via inter-nucleon forces. These forces emerge from strong interactions between constituent quarks and gluons, whose dynamics is described by the quantum field theory of Quantum Chromo Dynamics (QCD). Unfortunately, QCD displays a non-perturbative character at low energies characterising the realm of nuclear structure. In this context, the systematic and controlled description of the atomic nucleus poses a formidable task. This longstanding (and still unanswered) problem is at the heart of the so-called ab initio approach to the nuclear quantum many-body problem. It requires:
i) modelling the inter-nucleon interactions entering the A-body Schrödinger equation (an eigenvalue equation for the Hamiltonian where A is the number of nucleons composing the nucleus) with a sound connection to QCD
ii) developing mathematical methods allowing for accurate and controlled approximations of the exact solutions of the A-body Schrödinger equation.
Three decades ago, the seminal work of S. Weinberg paved the way for a systematic theory of inter-nucleon interactions anchored into QCD. He created a mathematical framework, called chiral effective field theory (EFT), which allows for constructing systematically improvable nuclear Hamiltonians1. Such Hamiltonians have nowadays replaced previous phenomenological models and have become the standard input to the A-body Schrödinger equation. Nevertheless, finding the solution of the Schrödinger equation for a large range of nuclei remains a highly non-trivial problem, both from a formal and a computational perspective. Therefore, such calculations have long been limited to light systems with mass number A ? 12.
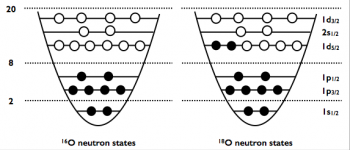
Figure 2: Neutron states of 16O (doubly closed shell) and 18O (singly open shell) in the standard non-interacting shell model. Filled (open) circles correspond to occupied (unoccupied) single-particle states in the ground-state reference state.
Expanding the exact solution
Over the past 15 years, mathematical methods expanding the exact solution with respect to a simple mean-field reference state have been designed and, thus, enabled the description of heavier nuclei up to tin isotopes (A =50). However, these methods have remained limited until recently to nuclei with specific numbers of protons and neutrons: the so-called doubly closed-shell nuclei. Indeed, to first approximation, a nucleus can be described by a state obtained by filling up protons and neutrons on two sets of shells that can only accept a specific number of them each. When the proton and neutron numbers are such that the upper neutron and proton shells are entirely filled, the corresponding nucleus is coined as ‘doubly closed-shell’ (see Fig. 2). These nuclei are relatively more stable and simpler to describe than their neighbours as they authorise the use of standard Slater determinants as reference states. In the past years, theoreticians from Irfu/DPhN have developed several different expansion methods allowing one to perform ab initio calculations of singly open-shell nuclei, i.e. nuclei whose upper proton or neutron shell is not fully occupied and that are relatively more challenging to solve for. This has extended the reach of ab initio calculations from a few tens to several hundreds of nuclei.
Breaking the symmetry of the Hamiltonian
The key idea behind these approaches is to allow the reference state to break a symmetry of the underlying Hamiltonian. For semi-magic nuclei, the relevant symmetry to be broken is the so-called U(1) global gauge symmetry, an abstract symmetry associated with the simple fact that nuclei are made of specific numbers of protons and neutrons. In these approaches, the system is first allowed to not have exactly Z protons or N neutrons in order to handle the complexity associated with the partially filled character of the upper shell. This idea leads to employing a so-called Bogoliubov reference state (solving the Hartree-Fock-Bogoliubov mean-field equations) that generalises the use of a simpler Slater determinant (solution of the well-celebrated Hartree-Fock mean-field theory). This allows to capture from the outset the superfluid character of singly open-shell nuclei. While the breaking of U(1) symmetry is a standard tool in simple mean-field descriptions, it had never been applied in beyond-mean-field methods aiming at an accurate solution of the A-body Schrödinger equation and, thus, allowing for ab initio calculations. The most recent formalism developed by theoreticians from Irfu/DPhN consists of a perturbative expansion around the particle-number-breaking Bogoliubov reference state and is, thus, coined as Bogoliubov many-body perturbation theory (BMBPT). In Fig. 3, a systematic comparison of BMBPT results with other state-of-the-art methods, among which one has also been developed by the same group ( ADC(2) ), is shown for three different isotopic chains. While it is obvious that BMBPT performs extremely well against existing methods for both binding energies and two-neutron separation energies, it does so for a computational price that is two orders of magnitude lower. This makes BMBPT an extremely useful candidate for performing large survey calculations across the nuclear chart, which enables in-depth testing of next-generation nuclear Hamiltonians. At the same time future extensions to even more challenging doubly open-shell nuclei are much simpler than in other frameworks.
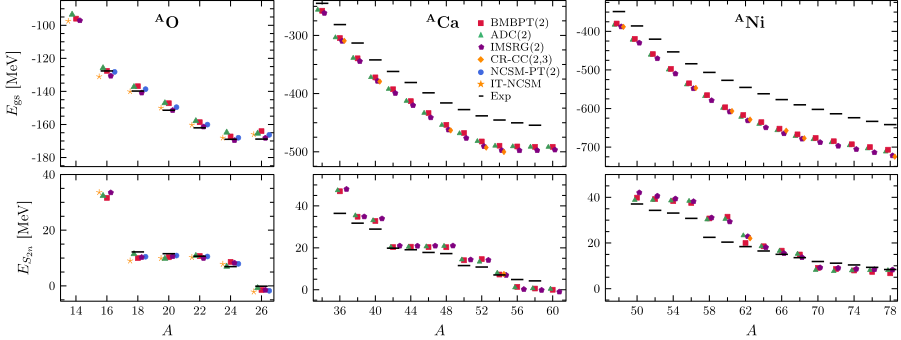
In summary, the theoreticians from Irfu/DPhN have added a new ab initio quantum many-body method dedicated to the ab initio description of mid-mass open shell nuclei that can compete with all previously available methods at a much lower computational cost. Being almost entirely developed at Irfu/DPhN, this newly designed method marks the increasing significance of the CEA theory group in the sector of ab initio nuclear structure theory.
[1] A. Tichai, P. Arthuis, T. Duguet, H. Hergert, V. Somà, R. Roth, Phys. Lett. B786 (2018) 195
Contact: Alexander TICHAI CEA-Saclay/Irfu/DPhN/LENA
1. Hamiltonian: mathematical operator describing the dynamics of interacting particles. In the case of the nuclear Hamiltonian, it is written as the sum of the kinetic energies of the A nucleons and the sum of the two-body, three-body, … interactions between the nucleons. Contrary to simpler cases, like Coulomb repulsion in electromagnetism, the strong interaction does not allow for writing down a closed analytical form of the corresponding potential in terms of spatial, spin and isospin degrees of freedom



