Since 2010 the question of the size of the proton is at the heart of a controversy between atomic physicists and hadronic physicists. Indeed, very precise measurements of atomic physics have concluded that the size of the proton is much smaller than expected, in very strong disagreement with the experiments of elastic scattering. In collaboration with the University of Perugia, a physicist from IRFU has investigated to find the reason for such a difference. The results have been published in European Journal of Physics A [3].
Metrology is the science that aims to measure, with the greatest possible precision, the constants of physics and to define standards for their measurement. Thus, for example, since 1983, the metre is defined as the distance travelled in vacuum by light during 1/299.792.458 of second. This definition of the meter is very general because it is based on the invariance of the speed of light perceived by different observers located in Galilean reference frames. In return, this definition uses our knowledge of the speed of light, which is necessarily limited by the precision of the instruments used to measure it and is therefore imperfect.
Two measurements, two sizes of the proton
In the same way, the precise knowledge of the size of the proton (about 1 fm) is extremely important because this particle is both the most stable known (its decay period is more than 1029 years) but also constitutes, as the nucleus of the hydrogen atom, the most abundant element in the universe. However, its size is at the heart of heated controversy because it cannot be measured directly, and needs to be extracted via different intermediate quantities accessible to measurement. The problem concerning the size of the proton is that these extractions lead to different conclusions!
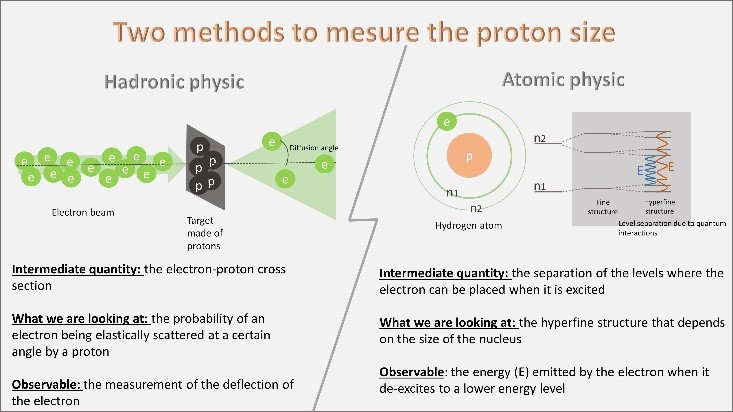
Figure 1: The two experimental methods used to deduce the size of the proton. Hadronic physics uses the elastic electron-proton cross section cross section, while atomic physics is interested in the influence of the proton size on the electronic levels.
Thus, the community of hadronic physicists uses as an intermediate quantity the measurement of the electron-proton elastic cross section, i.e. the probability that an electron is elastically scattered at a certain angle by a proton (see figure 1, left) and deduce the size of the proton. This probability depends on the charge distribution of the target seen by the electron during the interaction. The size of the proton can thus be deduced.
The atomic physics community uses the separation of electronic levels in the hydrogen atom (hyperfine structure of the atom, field of atomic physics). Indeed each electronic level separates into substructures because of quantum perturbations, it is the 'hyperfine separation of quantum states' of hydrogen. The electrons can only occupy these levels defined according to their energy. The energy emitted by the electron when it changes levels (E on the figure) contains a corrective term that depends on the distance of the orbit from the core of the atom, the proton.
Until 2010, measurements by both communities were in agreement: the Committee on Data for Science and Technology (CODATA) recorded a measured proton size value rpe =0.8775±0.0051 fm from atomic physics in agreement with the elastic scattering results rpel=0.886±0.008 fm, affected, however, by a larger uncertainty [1].
By orbiting the proton not with an electron but with a muon, 200 times heavier than the electron, atomic physicists have challenged this agreement: under the effect of the weight of the muon, the muonic hydrogen is much more compact and the muon, orbiting more closely around the nucleus, feels the charge of the proton much more strongly. The corrective terms to the orbits become more important and allow a very precise determination of the size of the proton that was found as rpm=0.84087±0.00039 fm, showing that the proton is much thinner than previously assumed [2], especially since this measurement has a much higher accuracy than the previous ones!
Experiments and theoretical studies have multiplied: in the camp of atomic physics, by measuring different transitions (i.e., the energy emitted by the atom when the electron or muon passes from one level to another) with electron and muon atoms, and in that of hadronic physics, by carrying out more and more precise experiments, in kinematic conditions where the electron disturbs the proton as little as possible.
The results are, to date, inconsistent, with some experiments confirming a thin proton, others a thick proton, and this in both fields. A physicist from IRFU, in collaboration with a colleague from the University of Perugia, decided then to critically revise the theoretical formalism underlying the extraction of the proton radius from cross section measurements of the electron proton elastic cross section. This study, published by EPJA [3], invalidates all the results obtained by elastic scattering beyond a certain accuracy by revealing a strong bias affecting the analyses.
Elastic diffusion & systematic error
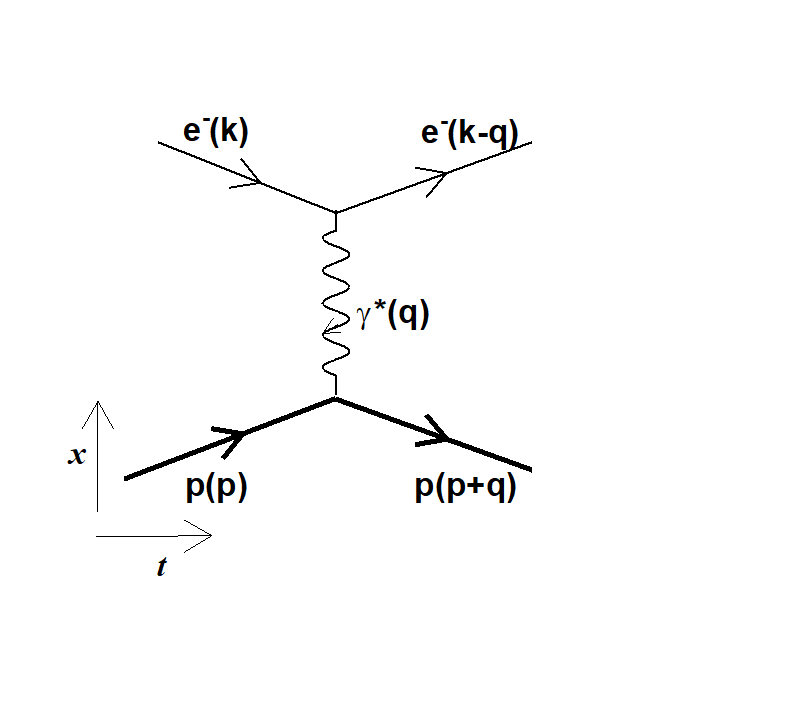
Figure 1: the elastic scattering between the electron (e-) and the proton (p) involves the exchange of a so-called virtual photon characterized by a four-momentum squared q².
Indeed, the elastic scattering of electrons on a proton implies the exchange of a so-called virtual photon, which is characterized by 'q2', the square of the energy-momentum four-vector, the quantity transferred from the electron to the proton (fig 2). The method to extract the proton radius requires the measurement of the electron-proton elastic cross section, at the lowest values of q2. This value for the elastic scattering is finite and the experiment aims at measuring as precisely as possible the effective cross sections at the smallest values of q2. Processing these results leads to determine the proton radius.
The effective cross-section is expressed in terms of 'form factors', quantities which parameterize the charge and magnetic distributions. The radius is then defined as the limit for q2->0 of the derivative of the charge form factor, which is dominant and is normalized to the value of the elementary charge (unity) at q2=0.
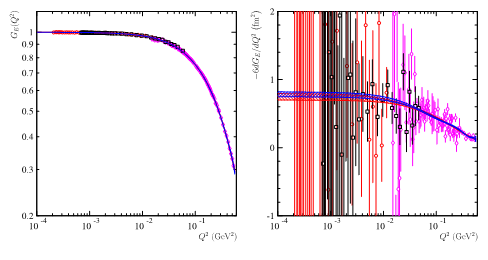
Reanalyzing the most recent and accurate data from the A1 collaboration in Mainz [4], and the PRad collaboration in JLab [5], (Fig. 3) the French-Italian team has shown that the value obtained by the extrapolation of the cross section to q2->0 depends on the interval of q2 where the data are selected and on the predefined function used for the fit of the data. The fluctuations on the reconstructed values of the radius become more sizable as the lower bound in q2 of the fit interval is small.
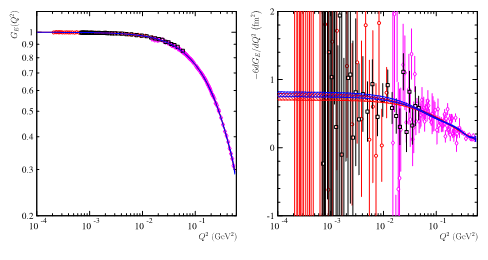
Fig 3: Data from CLAS [5] at q2=1.1 GeV2 (red circles) and q2=2.2 GeV2 (black squares) and Mainz [4] (pink diamonds), on the left the electric form factor, on the right its numerical derivative multiplied by -6, that gives directly the value of the radius. The blue and red curves give the most probable ranges obtained with two fits by polynomials of degree 7 of a real variable (blue curve), and the other extrapolated in the complex plane (red curve).
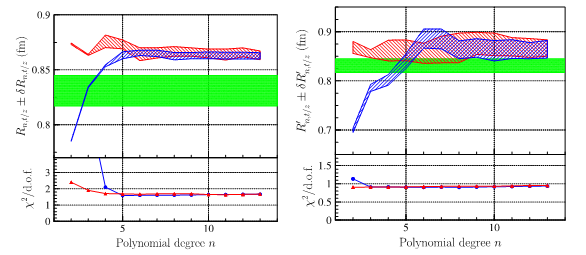
Fig 4: Radius extracted by the two different parameterizations, as a function of the degree of the polynomial, left by a fit on the form factor, right by the fit on the numerical derivative. The green band represents the result published by the JLab-PRad experiment. The lower frame represents 'the goodness of fit': we note its stability above degree 5 for the radius, and degree 3 for the derivative.
In particular, the reconstructed values from different fit functions (Fig. 4) show numerical errors on the derivative (proportional to the radius) that are much larger than the errors displayed by the experiments. This systematic error in the reconstructed value of the radius ends up being much larger than the error attributed to the measurement of the cross section, and reflects a conceptual problem: the radius is not measured but extracted from an intermediate quantity, itself extrapolated! (via the formalism of the interacting particle system for the treatment of two-body scattering). However, when the electron approaches the proton to probe its size, the system becomes bound. The limit q2=0 is obtained when the angle or the energy of the emitted electron are zero. In the first case the electron is emitted at zero degrees and therefore 'does not see' the target. In the second case, the electron is not emitted and is captured by the proton, which prohibits the use of a two-body formalism since the resulting system is a compound nucleus.
Can we overcome these problems of extrapolation? Nothing is less certain because the extraction of the radius is based on a physical mechanism of two-body diffusion (here the proton and the electron). However, if the energy of the electron becomes too low, it is captured by the proton, forming a hydrogen bound state which then becomes a one-body problem. The scattering phenomenon stops, and deprives the physicists of additional data to extract the radius of the proton.
Thus, the French-Italian team concludes that elastic scattering cannot be considered an accurate method to deduce the mean square radius of a particle, which is a static property. The ball is now in the court of atomic physics!
References:
[1] The NITS Reference on Constants, Units, and Uncertaity. https://
physics.nist.gov/cgi-bin/cuu/Value?rp|search_for=proton+rms.
[2] R. Pohl et al., Nature 466, 213 (2010).
[3] S. Pacetti and E. Tomasi-Gustafsson, Eur. Phys. J. A57 (2021) 72 et Eur. Phys. J. A56 (2020) 3.
[4] J.C. Bernauer et al. (A1 Collaboration), Phys. Rev. C 90, 015206 ( 2014)
[5] W. Xiong et al., Nature 575, 147 (2019).
Contact: Egle Tomasi-Gustafsson
• Structure of nuclear matter › Atomic nucleus
• The Nuclear Physics Division
• Nucleon Structure Laboratory (LSN) - The internal structure of hadrons