Une équipe internationale conduite par des chercheurs du Service d’Astrophysique-Laboratoire AIM du CEA-Irfu vient de mettre au point une nouvelle méthode permettant d’améliorer considérablement la reconstruction des images obtenues par les nouveaux radiotélescopes de très grande taille, consitués d'un réseau de multiples antennes. Fondée sur une nouvelle approche dérivée des mathématiques appliquées et inspirée d'une théorie d'échantillonnage récente basée sur la parcimonie du signal [1], cette méthode a permis de reconstruire des images de sources ponctuelles avec une résolution angulaire deux fois meilleure que celle obtenue par des méthodes classiques, ouvrant la voie à une "imagerie "super-résolue". Ces résultats sont publiés dans la revue Astronomy & Astrophysics de mars 2015.
Radiotélescopes géants
Dans le but d’améliorer considérablement la détection de sources d’ondes radio faibles (sensibilité) et d’augmenter la qualité des images (résolution spatiale), plusieurs projets de radiotélescopes géants sont actuellement en cours de réalisation ou en projet.
LOFAR (pour "LOw Frequency ARray" - "Réseau à basse fréquence") est un grand réseau d’antennes déjà en cours de fonctionnement et qui comportera à la fin de son installation environ 25 000 antennes regroupées en 48 stations dans 5 pays différents (Pays-Bas, Allemagne, Royaume-Uni, France et Suède).
SKA (pour "Square Kilometre Array" - "Réseau d'un kilomètre carré"), dont la construction vient d’être décidée en Afrique du Sud et Australie et qui devrait être en opération à partir de 2020, comportera également plusieurs dizaines de milliers d’antennes dont la surface collectrice totale sera d'un million de m2.
Vision d’artiste des antennes du radiotélescope géant SKA dont la construction est prévue à partir de 2020 en Afrique du Sud et Australie. Crédits: SKA Organisation
Ces grands radiotélescopes sont des interféromètres. Constitués d’un réseau d’antennes connectées et réparties sur de grandes distances, ils permettent d’atteindre une résolution spatiale équivalente à celle d'une antenne unique dont la taille est la distance maximale entre les antennes. En contrepartie, il existe une information « manquante » qui correspond à l’espace vide entre les antennes.
Pour pallier cette limitation, les radioastronomes font appel aux techniques mathématiques de reconstruction d’image. Les chercheurs de l’équipe Cosmostat du Service d’Astrophysique-Laboratoire AIM ont choisi de mener une étude comparative de performance entre différents algorithmes d'imagerie actuels, incluant une nouvelle méthode basée sur le principe de parcimonie [1].
Imagerie super-résolue
Appliquée à l'imagerie par interférométrie radio, cette approche a permis de reconstruire convenablement des images de sources ponctuelles (avec une photométrie correcte) tout en amenant un gain d'un facteur 2 en résolution angulaire par rapport aux méthodes classiques d'imagerie, permettant ainsi d'atteindre une imagerie "super-résolue". Après avoir mené des tests de validations sur des simulations, cette méthode a été utilisée sur des vraies données obtenues avec le radiotélescope LOFAR. Il a été possible de faire l'image de sources radio étendues, notamment de l'émission radio des lobes de la célèbre source Cygnus A. La résolution spatiale variant en raison inverse de la fréquence des ondes radio, la comparaison a été faite avec des données obtenues à plus haute fréquence (et donc plus haute résolution spatiale).
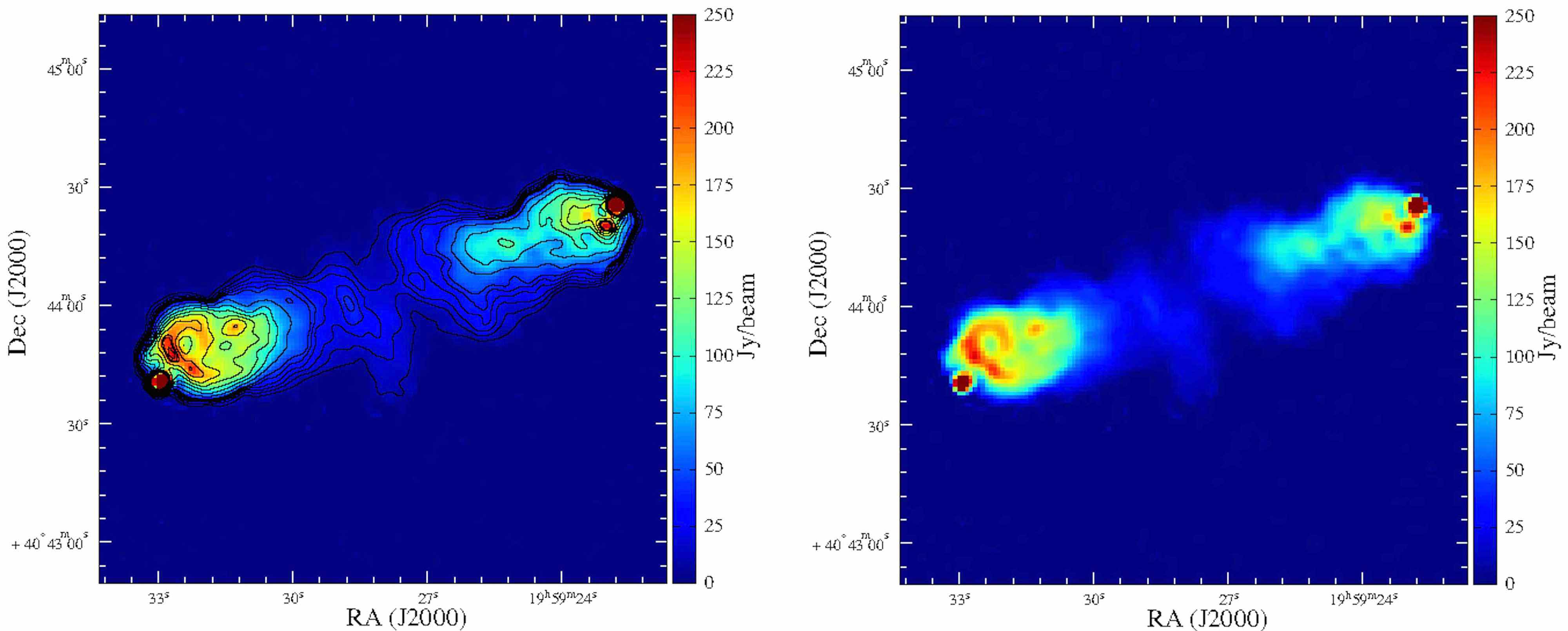
Cygnus A est l'une des radiogalaxies les plus brillantes et les plus célèbres. Située à environ ∼750 millions d'années-lumière de la Terre, elle est considérée comme possédant en son centre un trou noir 2.5 milliards de masse solaire générant deux jets symétriques de part et d’autre du trou noir, sources d’ondes radio.
A gauche, l’image radio sur laquelle a été superposée les données obtenues par le radiotélescope VLA à haute fréquence (327.5 MHz) avec une résolution de 2,5 secondes d’arc (contours). A droite, l’image LOFAR, obtenue à plus basse fréquence avec une résolution originelle de 5,5 secondes d’arc, est reconstruite par une méthode basée sur la parcimonie du signal. La majorité des structures reconstruites correspond à des structures observées à plus hautes fréquences, montrant une résolution angulaire effective de 2,8 secondes d’arc. Crédits CEA_Sap
L'image LOFAR, obtenue à une fréquence de 150 MHz, a été reconstruite par la méthode de parcimonie et comparée à l'image de la même radiogalaxie obtenue avec le Very Large Array, à une fréquence deux fois plus élevée (325 MHz). Les deux images présentent clairement le même qualité de détails. Les structures "super-résolues" à l'intérieur des lobes coïncident avec de vraies structures observées aux hautes fréquences, validant ainsi la capacité de cet méthode à reconstruire fidèlement des sources.
Le développement de cette technique ne s'arrête pas là et de nouvelles versions sont en préparation. Elles permettront, d'une part, de détecter des sources radio transitoires de manière non-ambigüe et, d'autre part, de permettre la reconstruction rapide d'images fiables et faiblement bruitées à partir de données parcellaires. Cette technique très générale peut s’appliquer aussi bien à la reconstruction d’images radio de sources (extra)galactiques, qu'à l'étude des inhomogénéités de l'univers primordial, mais également à l’ étude des sources radio du système solaire et même à la détection d'émissions radio transitoires de systèmes exoplanétaires.
Contacts : Julien GIRARD, Jean-Luc STARCK, Stephane CORBEL
Publication : "LOFAR Sparse Image Reconstruction"
H. Garsden, J. N. Girard, J. L. Starck, S. Corbel et al., publié dans la revue Astronomy & Astrophysics de mars 2015 pour une version en ligne (A&A PDF file)
voir aussi - Les défauts du fond diffus de l'univers sont-ils réels ? (04 août 2014)
- L'image la plus complète de la première lumière de l'Univers (27 janvier 2014)
[1] Parcimonie : Qualité d’un signal à pouvoir être représenté, dans un dictionnaire donné, par un petit nombre de coefficients significatifs. Les coefficients significatifs permettent de capter l’essentiel de l’information utile d’un signal et permettent à eux seuls de reconstruire un signal approché de bonne qualité (ce principe est à la base de la compression de données, et notamment d’images).
Rédaction : J.N. Girard, J.M. Bonnet-Bidaud
