En 2019, une première tomographie muonique avait été réalisée à partir de plusieurs projections 2D, via une collaboration avec l’Université de Florence. Les limitations restaient malgré tout nombreuses, car l’objet imagé ne faisait qu’une vingtaine de centimètres, avec des contrastes de densité très élevés (briques de Plomb), et un seul télescope fixe fonctionnant dans le mode très particulier de l’absorption. Une à une, toutes ces limitations ont été levées via une refonte complète des algorithmes et une optimisation des temps de calcul. Il est désormais possible de reconstruire la structure 3D de structures de plus de 100 mètres, et ce avec des écarts de densités réalistes et un nombre quelconque de télescopes fonctionnant dans le mode le plus général de la transmission. A titre d’illustration, le nombre d’éléments de matrice du système à résoudre est ainsi passé d’environ 10 millions pour la version de 2019 à plus de 20 mille milliards aujourd’hui.
Introduction
L’imagerie muonique, qui utilise le rayonnement cosmique naturel, est une méthode non invasive permettant en particulier de sonder l’intérieur de grandes structures. Dans les cas les plus courants, ces mesures fournissent une image 2D de la densité moyenne d’un objet, en estimant le flux de muons l’ayant traversé (mesures dites en transmission). L’observation d’écarts de densité sur une image ne permet donc pas de positionner en 3D une sous-structure, qui a minima doit être obtenue par triangulation depuis plusieurs points d’observation. La triangulation peut se révéler longue et fastidieuse, surtout si plusieurs sous-structures doivent être identifiées. L’idéal est alors de pouvoir combiner les images 2D pour obtenir une tomographie de l’objet. Dans le cas le plus général de l’imagerie muonique, de nombreuses difficultés surgissent :
- Faible nombre de projections dû au temps d’acquisition nécessaire pour les grands objets (plusieurs semaines à plusieurs mois)
- Non-unicité de la solution (comme la plupart des problèmes inverses) et nombre de mesures très inférieur au nombre d’inconnus du système
- Absence de mesure de flux en ciel ouvert, et nécessité de s’appuyer sur des outils de simulation (qui doivent donc reproduire les données réelles avec une grande précision)
- Taille gigantesque de la matrice du système à résoudre, impliquant des ressources CPU et des temps de calcul très élevées
Une muographie 2D d’une structure 3D (la pyramide de Khéops).
Une première étape a été franchie l’an dernier avec la tomographie d’un petit objet en Plomb [1]. La stratégie était de résoudre de manière itérative le système suivant :
Où 
est le vecteur des densités dans chaque voxel du volume à imager (donc le vecteur des inconnus), 
est le vecteur des opacités mesurées dans chaque direction d’observation, et 
est la matrice de distance, calculable une fois définis les voxels et les directions d’observation (à titre d’illustration, cette matrice comportait environ 6 millions d’éléments pour le petit objet imagé en 2019). L’algorithme de reconstruction est basé sur le SART (Simultaneous Algebraic Reconstruction Technique [2]) dont chaque itération consiste à mettre à jour la densité du voxel v en estimant un écart de densité via l’équation :
Où 
est le nombre de mesures et :
Reconstruction 3D de grands objets
L’algorithme ci-dessus peut tout d’abord être généralisé à plusieurs télescopes ou prises de vue, en calculant la matrice et le vecteur de chaque position, puis en les concaténant verticalement, au prix bien sûr d’une augmentation significative de la taille du système. En revanche, et contrairement aux mesures en absorption, la transmission ne fournit pas directement , mais un flux de muons transmis. Ce flux doit donc d’abord être normalisé en un facteur de transmission via des simulations à ciel ouvert (c’est-à-dire sans l’objet) de chaque position, qui utilisent ainsi une paramétrisation du flux différentiel de muons. Puis ce facteur de transmission est lui-même converti en une opacité au moyen d’une calibration ad hoc obtenue avec Geant4.
Un aspect essentiel de ce problème est le temps de calcul associé à sa résolution. La reconstruction du petit objet imagé l’an dernier ne prenait que quelques minutes sur un seul PC, et n’a donc pas nécessité d’optimisation particulière. Lorsque la première version du code généralisé aux grandes structures a été fonctionnelle, il a été réalisé que le temps de reconstruction d’un objet de la taille d’une pyramide avec une résolution de 50 cm prendrait sur le même PC… 47 ans ! Sans compter les problèmes de gestion de mémoire. Plusieurs optimisations ont donc été nécessaires sur le calcul et l’accès à cette matrice, mais aussi sur la rapidité de convergence de l’algorithme, avec à la clé une réduction du temps de calcul d’un facteur 15 000.
Pour illustration et validation de la méthode, une première reconstruction a été effectuée avec les données simulées d’un cube de 50 m de côté, de densité d=2, et contenant lui-même une cavité cubique de 15 m de côté. Neuf positions de télescopes sous le cube ont été simulées, correspondant chacune à un mois d’acquisition. Un volume de 80 m de côté englobant cet objet a été découpé en voxels de 0,5x0,5x2m3. La muographie de chaque position a elle été découpée en 10 000 mesures indépendantes, résultant en une matrice comprenant environ 90 milliards d’éléments. La figure ci-dessous montre la tomographie en tranche de l’objet reconstruit après 150 000 itérations, correspondant à 10 heures de calcul. On distingue parfaitement les limites transverses du grand et du petit cube, avec une résolution inférieure au mètre. Compte tenu de l’absence de prises de vue sur le côté, leurs limites verticales sont nécessairement moins nettes.
Figure 1 : tomographie 3D obtenue à partir des 2 cubes simulés et 9 positions de télescope. Les images montrent la distribution de la densité reconstruite dans une tranche horizontale, à différentes hauteurs.
Afin de valider ce code dans des conditions extrêmes, un deuxième test a été réalisé en simulant l’ensemble des données prises par les télescopes du CEA à l’intérieur de la pyramide de Kheops (11 positions). La pyramide définie dans la simulation inclue tous les vides connus actuellement, ainsi qu’une hypothèse du North Face Corridor détecté en 2016 par l’Université de Nagoya. Le volume à imager est dans ce cas un gigantesque parallélépipède de 230m de côté et 140m de haut, et chaque muographie a été découpée en 40 000 mesures indépendantes. Le nombre d’éléments de matrice du système à résoudre atteint alors 26 000 milliards (un nombre pharaonique !). Suite à l’optimisation de la convergence de l’algorithme, la reconstruction 3D prend environ deux jours sur une machine d'un centre de calcul. A noter que dans ce cas, le vecteur de densité est initialisé en supposant une pyramide pleine et parfaite, ce qui correspond à une information visible depuis l’extérieur. La figure ci-dessous montre un zoom de l’image reconstruite au niveau des Chevrons où le NFC a été simulé. En dépit du fait que ce système comporte 130 fois plus d’inconnus que d’équations, l’algorithme réussit à reconstruire la forme de la zone vide devant les Chevrons (où de nombreuses pierres ont été enlevées au fil des siècles), ainsi que le NFC simulé.
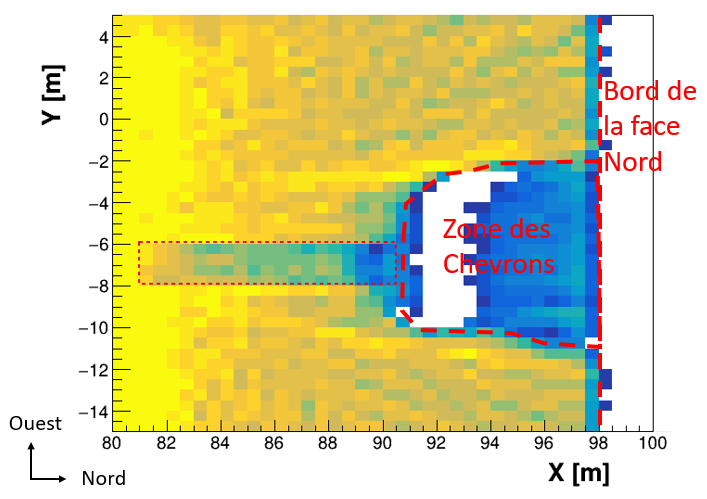
Figure 2 : distribution en densité obtenue au voisinage de la zone des Chevrons (entre Z=18.5 et Z=22.5m). En plus de la zone des Chevrons et de sa forme asymétrique Est-Ouest, l’algorithme de tomographie a correctement identifié et reconstruit une sous-densité correspondant au couloir simulé, dont la position est représentée par le rectangle rouge fin.
L’utilisation de cet algorithme sur les données réelles de la pyramide a également permis de reconstruire cette zone de manière satisfaisante, et les données seront publiées prochainement. Incidemment, cette méthode de reconstruction n’a plus besoin d’un modèle géométrique de l’objet en amont pour comparer données et simulation, puisque cette géométrie est produite directement par l’algorithme. D’autres grandes structures sont actuellement sondées par les télescopes à muons de l’Irfu, en particulier un réacteur nucléaire, et pourront donc à terme être imagées en 3D.
Références :
[1] : http://irfu.cea.fr/Phocea/Vie_des_labos/Ast/ast.php?t=fait_marquant&id_ast=4621
[2] : A. C. Kak, M. Slaney and G. Wang, "Principles of computerized tomographic imaging." Medical Physics 29.1 (2002): 107-107. Chapter 7
Contact : S. Procureur (Irfu/DPhP)
