Le cisaillement créé par les grosses structures modifie la dynamique des petites échelles qui en retour induisent un forcage sur les grandes échelles.
Il est donc indispensable dans toute simulation numérique de prendre en compte l'évolution et les caractéristiques de ces petites échelles. Or, dans la majorité des problèmes - en particulier dans les applications astrophysiques - , il est matériellement impossible de simuler toutes les échelles impliquées dans la dynamique. De plus, le faible intéret pratique des petites échelles ne justifie pas le coût élevé de leurs calcul.
C'est pour ces deux raisons que sont développés des modèles LES (Large Eddy Simulation) qui ont pout but de calculer directement la dynamique des grandes échelles en indroduisant une modélisation des plus petites. Nous avons développé une modélisation des petites echelles basée sur un développement en multi-échelles des équations régissant le fluide.
Le premier ordre du développement donne l'équation d'évolution des petites échelles qui traduit la concervation d'une quantité appelée enstrophie (le carré de la vorticité).
Le deuxieme ordre donne l'équation de base des grandes échelles à laquelle vient s'ajouter le terme de forcage induit par les petites échelles.
La méthode consiste donc à résoudre simultanément ces deux équations.
L'équation des petites échelles est résolue par une méthode particulaire appelé "Particles In Cells" où l'enstrophie est discrétisé en un grand nombre de particules véhiculées par les grandes structures du fluide.
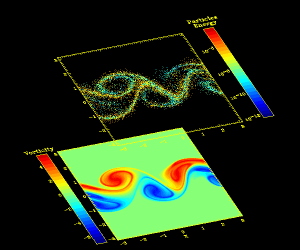
Résultat d'une simulation avec modélisation des petites échelles.
Le graphe du bas représente le champs de vorticité obtenu dans une portion de jet alors que celui du haut permet de visualiser l'évolution d'une partie des particules modélisant les petites échelles correspondantes (leur couleur étant proportionnelle à leur niveau d'énergie).(600x500 25Ko)
Les grandes échelles sont, quant à elles, résolues par une methode pseudo-spectrale sur un domaine carré périodique.
Dans la turbulence 2D, l'enstrophie cascade vers les plus petites échelles, il est donc nécéssaire d'adjoindre à ce modèle une procédure de transfert de l'enstrophie des grandes échelles vers les plus petites et réciproquement.
Cette procédure est réalisée en concervant simultanément l'enstrophie et l'énergie totale du système. Ce modèle permet de mettre en évidence l'importance de l'anisotropie des petites échelles dans leurs réactions sur les grandes structures du fluide.Les résultats du modèle ont été comparés avec succés à des résultats issus de simulations directes (sans modélisation) à haute résolution.
Une adaptation de notre méthode au calcul de la turbulence dans la nébuleuse protoplanétaire est en cours.

