En fait une telle vitesse peu être interprétée en termes d'illusion relativiste dans l'observation des éjections car elles se déplacent à une vitesse proche de celle de la lumière. L'éjection se déplace si vite qu'elle rattrape presque ses propres radiations.
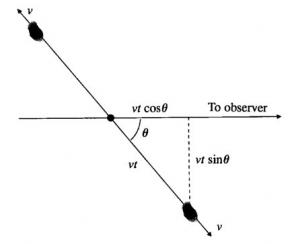
Apres un temps t suivant l'éjection, les nuages de plasma de vitesse réelle v, se sont déplacés d'une distance v.t . Vu en projection par l'observateur, ce déplacement semble être de v.t.sin q , q étant l'angle entre la ligne de vue et l'axe de l'éjection (voir le dessin). Cependant comme la condensation est maintenant plus proche d'une distance v.t.cos q , le temps t' pour que l'observateur voit la condensation se déplacer de l'origine a sa position actuelle est plus petit que t et est donné par
t' = t ( 1 - (v/c).cos q )
(1)
La vitesse apparente de la condensation qui approche est alors de
va = ( v.sin q ) / ( 1 - (v/c).cos q )
(2)
On remarque qu'il est possible que va soit supérieur à c. Par un raisonnement similaire, la vitesse apparente de la condensation qui s'éloigne est
vr = ( v.sin q ) / ( 1 + (v/c).cos q )
(3)
Si on peut mesurer le mouvement propre dans le ciel des deux éjections, ont obtient deux équations indépendantes : µa et µr en rad/s D étant la distance de la source
µa = ( v.sin q ) / ( 1 - (v/c).cos q )D
(4)
µr = ( v.sin q ) / ( 1 + (v/c).cos q )D
(5)
En mesurant la longueur d'onde des raies spectrales émises et la longueur d'onde au repos des éjections, on peut choisir une troisième équation entre les deux suivantes :
la / lrepos = ( 1 - (v/c).cos q ) / (1 - (v/c)2 )1/2
(6)
lr / lrepos = ( 1 + (v/c).cos q ) / (1 - (v/c)2 )1/2
(7)
On peut résoudre ce systeme de trois equations et trouver les inconnues v, q, D. Pour commencer il est possible de trouver une limite supérieure à la valeur de la distance D à partir des mesures du mouvement propre des deux condensations. Les équations (4) et (5) sont équivalentes à :
b.cos q = ( ma - mr ) / ( ma + mr )
(8)
D = c.tan q.( ma - mr ) / ( 2.ma.mr )
(9)
On peut déterminer le produit b.cos q sans connaitre la distance D. Comme ma=17,6 +/-0,4 mas d-1 et mr=9,0 +/-0,1 mas d-1, on trouve que b.cos q=0,323 +/-0,016. Ce dernier résultat implique que cos q³0,323 ou q£71°, et que b³0,323. En substituant la limite supérieure q£71° dans l'équation (9), et en remarquant que 1 mas d-1 = 5,61.10-14 rad/s, on obtient à partir des contraintes relativistes une limite supérieure de la distance qui est D£13,7 kpc. Les mouvements observés se situent donc dans notre Galaxie.
La distance cinématique à GRS1915+105 a été déterminée par l'absoption à 21cm par l'atome d'hygrogène le long de la ligne de vue. La source est proche du plan galactique ( l=45,37°, b=-0,22° ) et au delà de 20 mag d'absorption optique. L'opacité de la région HI est similaire pour GRS1915+105 et G45.46+0.06 qui est la plus proche région HII du ciel avec une distance cinématique connue. La colonne densité de HI le long de la ligne de vue à GRS1915+105 est N(HI)=(1.73x1022).(Ts/100K) (où Ts est la température de rotation), qui vaut 1,42 fois la colonne densité le long de la ligne de vue à la région HII G45.46+0.06. Puisque la région HII se situe à ~8,8 kpc, et en supposant que l'absorption de HI par unité de longueur est constante, on trouve que GRS1915+105 se situe a une distance D=12,5 +/-1,5 kpc, ce qui est cohérent une absorption optique de 20 mag.
A cette distance les mouvements propres de la condensation qui avance et de celle qui s'éloigne impliquent des vitesse apparentes dans le plan céleste de respectivement 1,25 +/- 0,15 et 0,65 +/- 0.08 fois la vitesse de la lumière. D'apres les équations (3) et (4) nous déduisons que les éjections se déplacent avec une vitesse réelle de b = 0,92 +/- 0,08 et sous un angle q = 70 +/- 2° par rapport à la ligne de vue.