De par sa proximité, le Soleil a une influence forte et directe sur la Terre et notre société technologique. En particulier, son activité magnétique et le vent de particules chargées perturbent l'environnement spatial autour de notre planète allant jusqu'à endommager nos satellites, voire, dans le cas d'éruptions solaires extrêmes, nos centrales électriques. Afin de pouvoir prédire et anticiper de tels phénomènes, il est nécessaire de comprendre l'origine de ces processus physiques. Aujourd'hui, il est admis que ces phénomènes dynamiques sont reliés à une dynamo turbulente interne distribuée dans et à la base de la zone convective solaire. Une approche prometteuse pour tester cette interprétation consiste à simuler de façon tridimensionnelle cette région du Soleil sur de gros calculateurs comme ceux du CEA au CCRT de Bruyères-le-Châtel.
Enjeux et Challenges de la Modélisation Dynamique du Soleil
Le Soleil est une grosse boule de gaz chaud et ionisé (plasma) tournant sur lui-même en 28 jours environ. Les 30% les plus externes en rayon sont animés en permanence de mouvements convectifs. Ces mouvements, sous l'influence des forces de Coriolis et de Laplace, sont turbulents et chaotiques. Cette région possède un large éventail de phénomènes magnétiques (cf. Figures 1, 4 et 5). Pour comprendre la dynamique turbulente et l'activité magnétique du Soleil, pouvoir l'anticiper et se protéger de ces incidences sur terre, il est nécessaire de posséder un modèle physique de son intérieur (radiatif et convectif) et de son atmosphère (partagée en photosphère, chromosphère et couronne).
Le modèle actuel des couches dynamiques externes repose sur la théorie de la dynamique des fluides et des plasmas (fluides conducteurs), aussi appelée magnétohydrodynamique (MHD). Cette théorie décrit le fonctionnement mécanique, hydrodynamique, thermodynamique et magnétique du plasma turbulent solaire à partir d'équations aux dérivées partielles non linéaires et couplées. Malheureusement, de tels systèmes d'équations n'ont pas encore à l'heure actuelle de solutions mathématiques exactes (analytiques) nous permettant de résoudre totalement le problème posé par la turbulence et l'activité solaire si aucune hypothèse simplificatrice n'est considérée. Cette difficulté résiste depuis plus de 50 ans et constitue un des challenges majeurs de l'astrophysique moderne et plus particulièrement de la dynamique des fluides astrophysiques. Il est donc nécessaire de développer des approches complémentaires pour progresser dans notre compréhension de ces phénomènes. Il convient :
1) de simplifier plus ou moins fortement le système étudié pour pouvoir le traiter analytiquement ou
2) de développer un programme informatique résolvant le système le mieux possible par approximation numérique
3) de cumuler les deux approches précédentes pour analyser un à un chaque aspect du problème
Il est certain que le développement d'ordinateurs dit massivement parallèle avec une puissance de calculs impressionnante (des dizaines de milliers de milliards d'opérations élémentaires par seconde ou Teraflops) encourage le développement de codes performants les plus réalistes possibles décrivant la magnétohydrodynamique des étoiles et du Soleil, voir du système Soleil-Terre. Le magnétisme solaire est de nature différente à l'intérieur de notre étoile (où le champ magnétique B est advecté par les mouvements) qu'il ne l'est dans son atmosphère (où le champ magnétique dicte (impose) la dynamique). Pour cette raison, la modélisation de la magnétohydrodynamique du Soleil a été séparée en physique solaire interne et externe. Très récemment des synergies sont apparues afin d'intégrer dans un protocole plus large tous les développements dans le domaine de la simulation MHD du Soleil. Il reste cependant encore beaucoup d'efforts avant d'arriver à un modèle complet.
Il convient de dresser ici un rapide panorama de l'état actuel des simulations multidimensionnelles en se limitant à la convection turbulente, i.e. interne, du Soleil. La principale raison de ce choix est que toute la dynamique atmosphérique du Soleil doit en partie son existence et sa variabilité à son couplage fort avec la dynamique interne. Ceci est particulièrement vrai du cycle de 22 ans d'activité magnétique et d'émergence des taches solaires (cf. section 3 et Figure 4).
Pour étudier la convection solaire, deux approches parallèles et complémentaires ont été menées; l'une modélisant de façon locale dans une géométrie cartésienne à très haute résolution une portion réduite de la convection de surface solaire, l'autre s'attaquant à la modélisation globale en géométrie sphérique à résolution plus modeste de l'ensemble de la zone convective (excepté les couches superficielles). La première méthode permet de décrire plus correctement la turbulence solaire et les propriétés microscopiques du plasma, au détriment de l'usage de la bonne géométrie et de la présence d'écoulements moyens globaux. La seconde a l'avantage d'ébaucher un modèle de circulation dans le Soleil, comme celui développé pour prédire le climat. C'est cette deuxième approche que nous allons décrire ici.
Simulations Numériques Globales de la Convection Turbulente Solaire
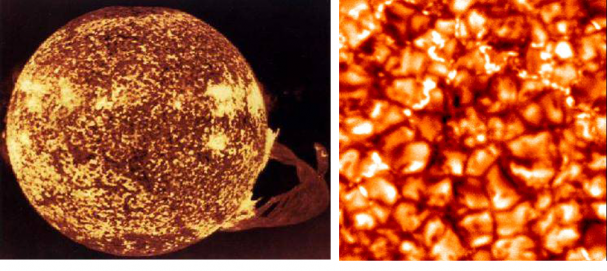
Le Soleil possède un aspect granuleux qui provient des mouvements convectifs turbulents transportant la chaleur vers sa surface. La figure 1 montre une vue globale du Soleil et un zoom sur les cellules convectives (les granules) couvrant toute sa surface et dont la taille caractéristique est de 1000 km. Cette granulation génère les ondes acoustiques qui sont utilisées comme diagnostic de la structure interne du Soleil.
Le large intervalle d'échelles spatiales et temporelles présent sur ces images (environ 6 ordres de grandeur par dimension) rend la modélisation numérique de la convection turbulente solaire difficile (on parle de problème numérique raide) même sur les ordinateurs actuels. II n'est donc pas encore possible de modéliser la granulation solaire avec l'approche globale discutée ici. Cependant, au gré des développements des ordinateurs, la résolution utilisée par les codes hydrodynamiques modernes atteint aujourd'hui un maillage de 4000 km de côté et 1000 km de profondeur, donc s'approchant de plus en plus de l'échelle spatiale de la granulation. La figure 2 représente les résultats de telles simulations numériques. On y voit le mouvement convectif (vitesse radiale/verticale) d'une sphère de gaz en rotation, à trois instants successifs, séparés de 5 jours, avec, en bleu, les flots descendants et, en jaune-rouge, les flots ascendants. On remarque clairement que les lignes de flots descendants sont plus étroites que les larges flots montants.
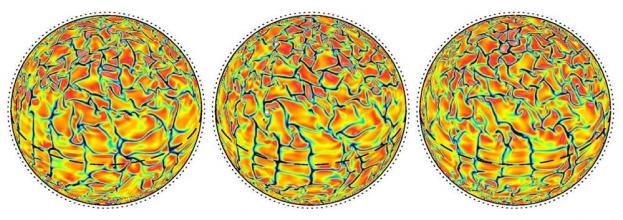
fig 2 : Evolution temporelle de la vitesse radiale dans une simulation globale 3-D de la convection sous l'influence de la rotation. En bleu les flots descendant et en jaune-rouge les flots montant. Chaque image est séparée par 5 jours. Les marqueurs A, B et C suivent des motifs convectifs particulièrement intéressants.
Les cellules à plus haute latitude évoluent, se mélangent entre elles et se disloquent par l'apparition de nouvelles structures. Aux interstices des lignes de flots descendants, on remarque des structures cycloniques, qui tournent (respectivement) dans le sens (contraire) des aiguilles d'une montre dans l'hémisphère sud (nord). Ces structures, dénommées panaches, représentent des tubes de vorticité (de rotation) intense et traversent toute la zone convective en profondeur. Plus prêt de l'équateur, on remarque que les motifs convectifs sont moins isotropes qu'à plus haute latitude et plus alignés avec l'axe de rotation (direction nord-sud). Ces structures sont également étirées et cisaillées par un écoulement horizontal à grande échelle: la rotation différentielle.
Comprendre la Rotation Différentielle Solaire
L'observation du Soleil révèle que sa surface tourne avec une vitesse de rotation qui varie en latitude, de 25 jours à l'équateur jusqu'à 35 jours aux pôles. Les modèles de convection en géométrie sphérique sous l'influence de la rotation, permettent d'étudier l'établissement d'un tel profil de rotation différentielle. Sous l'influence de la rotation, les mouvements convectifs s'organisent différemment, par exemple en s'alignant et s'inclinant en direction de l'axe de rotation. C'est particulièrement vrai des panaches convectifs qui sont à l'origine de l'accélération équatoriale observée dans les simulations.
Nous représentons Figure 3, dans une coupe dans le plan méridien, la rotation différentielle en profondeur et latitude accompagnant les mouvements convectifs représentés Figure 2. Nous constatons que toute la bande équatoriale tourne plus rapidement et que la rotation différentielle ralentit jusqu'à tourner 30% moins vite aux pôles. Vers 45-70° de latitude, la rotation est constante le long des lignes radiales (conique), comme l'indique les lignes les plus horizontales dans le graphe de droite représentant des coupes radiales à latitude fixée de ?. Cette rotation différentielle est à l'origine de l'advection des cellules convectives (vers la droite à l'équateur, et vers la gauche aux latitudes plus élevées). L'accord entre les simulations globales de la convection avec les observations héliosismiques est raisonnable. Cela démontre que les modèles de convection turbulente tridimensionels commencent à devenir réalistes pour décrire les mouvements aux grandes échelles observés dans le Soleil. Le profil de rotation est établi par la redistribution continue du moment cinétique contenu dans la coquille convective en rotation. En particulier, les corrélations des 3 composantes de la vitesse ou Tenseur de Reynolds, transportent le moment cinétique depuis les hautes latitudes vers l'équateur accélérant ainsi cette portion de la zone convective.
Une caractéristique importante du profil de rotation solaire est qu'il devient constant dans l'intérieur radiatif, la transition entre rotation différentielle et solide se faisant très rapidement dans une zone a très fort cisaillement : la tachocline. Cette couche limite est cruciale pour comprendre la dynamo solaire, et nous prévoyons d'adjoindre aux simulations de la zone convective une zone stable la modélisant.
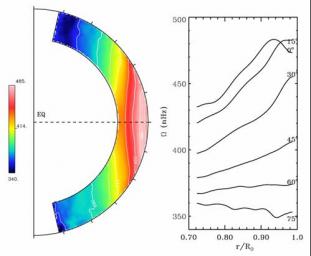
fig 3 : Rotation différentielle accompagnant les motifs convectifs représentés Figure 2. En rouge les zones de rotation rapide et en bleu celles en rotation lente. L'accord avec l'héliosismologie est raisonnable, avec un contraste de rotation différentielle de l'ordre de 30%, des moyennes latitudes pratiquement constantes le long de lignes radiales et des régions polaires tournant particulièrement doucement.
Propriétés et Rôle du Champ Magnétique
L'activité magnétique solaire est fascinante par sa diversité, comme l'atteste les Figures 4 et 5. Tout d'abord, la figure 4 montre le diagramme papillon d'émergence des taches solaires fonction de la latitude et du temps au cours de ces dernières décennies (1975-2002). On observe la succession de bandes se propageant vers l'équateur et alternant leurs signes tous les 11 ans, formant ainsi comme des ailes de papillons. La conséquence directe d'une telle observation est que l'axe du champ magnétique solaire doit forcément s'inverser tous les 11 ans pour accompagner l'alternance des polarités (le fameux cycle des 22 ans (+ / - / +)), tel un aimant dont les pôles s'inverseraient régulièrement.
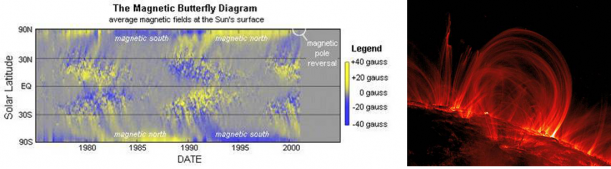
fig 4 : Diagramme papillon d'émergence des taches solaires au cours des 3 dernières décennies. On y voit clairement la migration équatoriale des taches au cours d'un cycle puis le renversement de polarité, le tout faisant un cycle complet de 22 ans.
fig 5 : Boucles magnétiques dans la couronne solaire. La topologie complexe des structures magnétiques dans la haute atmosphère solaire facilite les reconnections des lignes de champ et génère des éruptions.
La Figure 5 représente une vue rapprochée de la haute atmosphère solaire (couronne), où des boucles de champ magnétique apparaissent, se développent et se reconnectent sans cesse, produisant ainsi des éruptions solaires avec peu d'éjection de matière. Il existe aussi des configurations de champ magnétique très complexes qui sont généralement reliées aux régions actives regroupant plusieurs groupes de taches solaires et possédant une structure en S ou N (selon l'hémisphère considéré sud ou nord). Dans ce cas, les éruptions sont beaucoup plus violentes et éjectent du plasma dans le milieu interplanétaire, on parle alors d'éjections de masse coronale. La régularité de l'émergence des taches solaires contraste avec l'imprévisibilité de la dynamique de surface du Soleil. Pourtant elles sont liées car plus on s'approche du pic d'activité solaire (5 à 7 ans après le dernier retournement), plus la fréquence et l'intensité des éruptions seront grandes. Ces phénomènes magnétiques apparaissent dans le Soleil car son gaz est conducteur. La présence de particules chargées (électrons, ions) dans le plasma solaire permet l'induction d'un champ magnétique par les mouvements convectifs. Cet effet dynamo est à l'origine du magnétisme observé. Afin de pouvoir comprendre la diversité de forme que revêt le magnétisme solaire, il est nécessaire de distinguer les évènements réguliers et ceux qui sont irréguliers. La théorie actuelle indique que la dynamo solaire est certainement séparée en dynamos petite et grande échelle. Le cycle des 22 ans, la loi de Hale définissant l'ordre des polarités des taches solaires, l'amplification de larges structures magnétiques dites toroïdales sont reliés à la dynamo grande échelle, organisée vraisemblablement dans la tachocline à la base de la zone convective. L'activité irrégulière et le champ magnétique désordonné (éruptions, point brillants, etc…) sont par contre le résultat de la turbulence présente dans l'enveloppe convective.
Nous avons entrepris, depuis quelques années, de considérer les effets du champ magnétique et de l'influence non-linéaire de la force de Laplace dans les simulations de convection turbulente en rotation.
L'introduction du champ magnétique complique le système d'équations physiques à résoudre et rend les codes numériques plus lents et plus complexes. Ainsi les modèles magnétohydrodynamiques du Soleil se font de plus en plus sophistiqués. Nous représentons Figure 6, la reconstruction potentielle du champ magnétique coronal d'une de nos simulations tri-dimensionelles de la zone convective solaire. On peut y reconnaître les structures en boucles resserrées observées dans la Figure 5, ainsi que des lignes s'ouvrant vers l'extérieur, un peu comme avec les trous coronaux solaires. La présence d'un champ magnétique fort, créé par induction dynamo, modifie la convection, les courants moyens et la balance d'énergie du système. Dans le cas représenté Figure 6, la rotation différentielle accompagnant la convection magnétisée a été réduite de près de 30% en amplitude. Les champs magnétiques créés apparaissent intermittents et leurs composantes fluctuantes dominent par 2 ordres de grandeur les champs moyens globaux. La polarité du champ magnétique dit poloïdal se renverse dans ces simulations mais sur une période trop courte de 500 jours. En fait, le champ moyen dit toroïdal du Soleil est proportionnellement plus important que dans les simulations et que le renversement ce fait tous les 11 ans, nos calculs confirment l'idée que de tels champs moyens et la régularité du cycle d'activité ne peut être généré dans une zone convective turbulente mais au contraire dans une zone cisaillée stable comme la tachocline.
La prochaine étape consistera donc à calculer des modèles MHD du Soleil incluant une tachocline et à moyen terme une atmosphère plus réaliste. Dans le futur, il deviendra possible de calculer en temps réel un modèle "météorologique" du Soleil et ainsi maîtriser plus efficacement les risques liés aux interactions Soleil-Terre. En attendant, les modèles actuels permettent de poser des jalons pour les développements futurs et d'interpréter la grande quantité de données observationnelles disponibles.
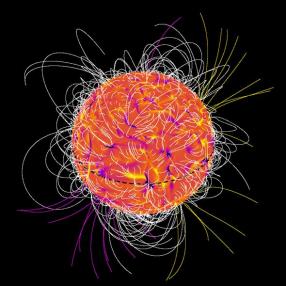
fig 6 : Reconstruction 3-D du champ magnétique coronal (approximation champ potentiel) à partir d'une simulation de dynamo turbulente. Les lignes blanches sont fermées et les lignes vertes et violettes correspondent aux lignes de champs ouvertes. L'image de fond représente la composante radiale du champ magnétique à un rayon de 0.95 rayon solaire.