Toute une zoologie de réactions entre en compétition lors d’une collision de noyaux à basse énergie: fusion, transfert de nucléon, excitation Coulombienne et nucléaire, cassure d’un noyau en plusieurs fragments... Il n’est pas rare qu’un des partenaires de collision ait une forme très éloignée de notre image classique de goutte liquide sphérique ou faiblement déformée. C’est d’ailleurs souvent le cas pour des noyaux exotiques. Par exemple, le noyau peut avoir un halo ou une peau de neutrons. Il peut aussi être constitué d’amas de nucléons, ou encore avoir une forme de banane ou de poire prononcée.
Développer une théorie capable de traiter de manière consistante l’ensemble de ces réactions en même temps que la variété des structures possibles constitue un défi en soi. Elle serait l’illustration d’une compréhension fine des phénomènes physiques à l’échelle du noyau. De plus, une telle théorie servirait de support aux expérimentateurs, tant pour reproduire les données et aider à leur interprétation, que pour prédire des taux de production de noyaux appartenant à la terra incognita nucléaire.
Des progrès considérables ont été réalisés depuis ces trente dernières années grâce, bien sûr, aux développements d’ordinateurs puissants, mais surtout à la persévérance de physiciens talentueux comme Paul Bonche qui a passé la plus grande partie de sa carrière au Service de Physique Théorique de Saclay. Précurseur dans l’application de théories microscopiques aux collisions nucléaires, il n’a cessé de développer et d’améliorer ces modèles pour atteindre un niveau de description réaliste tant de la structure nucléaire que des mécanismes de réaction.
Son code dynamique microscopique le plus évolué utilise la théorie Hartree-Fock dépendant du temps (TDHF) en trois dimensions. Il s’agit d’une théorie de champ moyen quantique où chaque fonction d’onde (associée à un nucléon) évolue dans un champ moyen généré par l’ensemble des nucléons. Celui-ci est déterminé à l’aide d’une interaction effective de Skyrme, de portée nulle mais non-locale. Les seuls ingrédients phénoménologiques du modèle sont les paramètres de cette force. Ceux-ci, au nombre de 10, sont ajustés pour reproduire la matière nucléaire infinie et des propriétés statiques d’un petit nombre de noyaux. Aucune quantité provenant de réactions n’entre en compte dans cet ajustement.
Un travail de test et d’optimisation de ce code pour l’adapter au centre ce calcul scientifique de Bruyères-le-Châtel a été effectué dernièrement avec une attention particulière aux conservations de symétries fondamentales telles que l’invariance Galiléenne et l’invariance par translation. Nous avons poursuivi le développement du code pour pouvoir traiter correctement les excitations Coulombiennes de longues portées, dont l’effet sur la fusion autour de la barrière peut s’avérer crucial. Il a aussi été modifié pour pouvoir utiliser l’état de l’art des forces de Skyrme développées par nos collaborateurs de l’IPN-Lyon, visiteurs fréquents de l’Espace de Structure Nucléaire Théorique (ESNT) à Saclay.
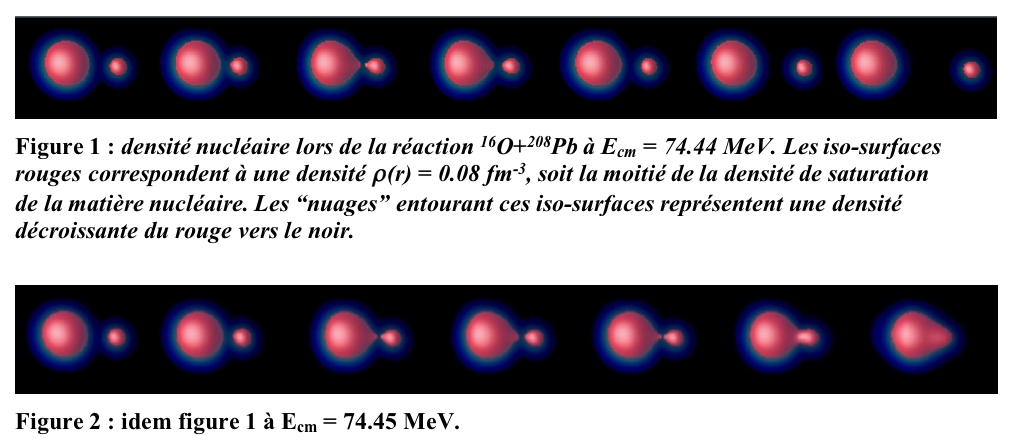
Les animations représentent la densité de nucléons dans le cas de deux collisions 16O+208Pb (voir aussi les figures) : l’une à une énergie de centre de masse de 74.44 MeV, juste en dessous de la barrière de fusion, et l’autre à 74.45 MeV, juste au dessus. Dans le premier cas, le système “hésite” à fusionner. Il forme un système di-nucléaire pendant un temps relativement long à l’échelle de la collision, durant lequel de la matière est échangée d’un noyau à l’autre. Puis la répulsion Coulombienne l’emporte et le système se sépare en deux fragments. Dans le deuxième cas, le système franchit la barrière de fusion grâce aux 10 keV supplémentaires pour former un noyau plus lourd. Ces calculs prédisent donc une barrière de fusion entre 74.44 et 74.45 MeV. Expérimentalement, celle-ci se distribue autour de 74 MeV, avec une largeur à mi-hauteur de 4 MeV. Il est donc frappant d’obtenir un tel accord entre l’expérience et une théorie dans laquelle, rappelons-le, aucun ajustement sur des mécanismes de réaction n’est effectué. Le même accord a été obtenu pour différents systèmes mesurés expérimentalement, avec des partenaires de masses et de formes variées. Enfin, les animations illustrent la richesse des phénomènes physiques décrits par TDHF: la diffusivité des surfaces nucléaires, la formation d’un col au commencement de la fusion, la forme octupolaire du système composé...
L’achèvement de ce code va donc permettre des études systématiques des mécanismes de réactions tels que ceux qui seront étudiés à SPIRAL2. Cependant le modèle a ses limites, comme de ne pouvoir traiter la fusion sous-Coulombienne ou de ne pas inclure l’appariement nucléaire par exemple. Il est donc nécessaire de persévérer dans la modélisation de la dynamique des systèmes à N-corps quantiques. Notre espoir se place dans le développement de théories allant au delà de l’approximation de champ moyen. Un des buts est de pouvoir traiter correctement l’effet tunnel par lequel la fusion sous la barrière peut avoir lieu. Dans ces théories, l’état du système n’est plus limité à un simple produit antisymétrique de fonctions d’ondes à une particule (cas d’un système de particules indépendantes), encore appelé « déterminant de Slater ». La fonction d’onde à N-corps doit en effet inclure des corrélations entre les nucléons, ce qui, en pratique, peut se faire en considérant une somme de déterminants de Slater. Nous développons actuellement un modèle de mélange dynamique de configurations, fortement inspiré par la méthode des coordonnées génératrices utilisée en structure nucléaire. Nous travaillons aussi sur l’inclusion de l’appariement nucléaire dans TDHF (thèse de Benoît Avez au Service de Physique Nucléaire de Saclay).
TDHF.doc (242 Ko)
animation_74_44MeV.gif (380 Ko)
animation_74_45MeV.gif (376 Ko)
 Toute une zoologie de réactions entre en compétition lors d’une collision de noyaux à basse énergie: fusion, transfert de nucléon, excitation Coulombienne et nucléaire, cassure d’un noyau en plusieurs fragments... Il n’est pas rare qu’un des partenaires de collision ait une forme très éloignée de notre image classique de goutte liquide sphérique ou faiblement déformée. C’est d’ailleurs souvent le cas pour des noyaux exotiques. Par exemple, le noyau peut avoir un halo ou une peau de neutrons. Il peut aussi être constitué d’amas de nucléons, ou encore avoir une forme de banane ou de poire prononcée.
Développer une théorie capable de traiter de manière consistante l’ensemble de ces réactions en même temps que la variété des structures possibles constitue un défi en soi. Elle serait l’illustration d’une compréhension fine des phénomènes physiques à l’échelle du noyau. De plus, une telle théorie servirait de support aux expérimentateurs, tant pour reproduire les données et aider à leur interprétation, que pour prédire des taux de production de noyaux appartenant à la terra incognita nucléaire.
Des progrès considérables ont été réalisés depuis ces trente dernières années grâce, bien sûr, aux développements d’ordinateurs puissants, mais surtout à la persévérance de physiciens talentueux comme Paul Bonche qui a passé la plus grande partie de sa carrière au Service de Physique Théorique de Saclay. Précurseur dans l’application de théories microscopiques aux collisions nucléaires, il n’a cessé de développer et d’améliorer ces modèles pour atteindre un niveau de description réaliste tant de la structure nucléaire que des mécanismes de réaction.
Son code dynamique microscopique le plus évolué utilise la théorie Hartree-Fock dépendant du temps (TDHF) en trois dimensions. Il s’agit d’une théorie de champ moyen quantique où chaque fonction d’onde (associée à un nucléon) évolue dans un champ moyen généré par l’ensemble des nucléons. Celui-ci est déterminé à l’aide d’une interaction effective de Skyrme, de portée nulle mais non-locale. Les seuls ingrédients phénoménologiques du modèle sont les paramètres de cette force. Ceux-ci, au nombre de 10, sont ajustés pour reproduire la matière nucléaire infinie et des propriétés statiques d’un petit nombre de noyaux. Aucune quantité provenant de réactions n’entre en compte dans cet ajustement.
Un travail de test et d’optimisation de ce code pour l’adapter au centre ce calcul scientifique de Bruyères-le-Châtel a été effectué dernièrement avec une attention particulière aux conservations de symétries fondamentales telles que l’invariance Galiléenne et l’invariance par translation. Nous avons poursuivi le développement du code pour pouvoir traiter correctement les excitations Coulombiennes de longues portées, dont l’effet sur la fusion autour de la barrière peut s’avérer crucial. Il a aussi été modifié pour pouvoir utiliser l’état de l’art des forces de Skyrme développées par nos collaborateurs de l’IPN-Lyon, visiteurs fréquents de l’Espace de Structure Nucléaire Théorique (ESNT) à Saclay.
Les animations représentent la densité de nucléons dans le cas de deux collisions 16O+208Pb (voir aussi les figures) : l’une à une énergie de centre de masse de 74.44 MeV, juste en dessous de la barrière de fusion, et l’autre à 74.45 MeV, juste au dessus. Dans le premier cas, le système “hésite” à fusionner. Il forme un système di-nucléaire pendant un temps relativement long à l’échelle de la collision, durant lequel de la matière est échangée d’un noyau à l’autre. Puis la répulsion Coulombienne l’emporte et le système se sépare en deux fragments. Dans le deuxième cas, le système franchit la barrière de fusion grâce aux 10 keV supplémentaires pour former un noyau plus lourd. Ces calculs prédisent donc une barrière de fusion entre 74.44 et 74.45 MeV. Expérimentalement, celle-ci se distribue autour de 74 MeV, avec une largeur à mi-hauteur de 4 MeV. Il est donc frappant d’obtenir un tel accord entre l’expérience et une théorie dans laquelle, rappelons-le, aucun ajustement sur des mécanismes de réaction n’est effectué. Le même accord a été obtenu pour différents systèmes mesurés expérimentalement, avec des partenaires de masses et de formes variées. Enfin, les animations illustrent la richesse des phénomènes physiques décrits par TDHF: la diffusivité des surfaces nucléaires, la formation d’un col au commencement de la fusion, la forme octupolaire du système composé...
L’achèvement de ce code va donc permettre des études systématiques des mécanismes de réactions tels que ceux qui seront étudiés à SPIRAL2. Cependant le modèle a ses limites, comme de ne pouvoir traiter la fusion sous-Coulombienne ou de ne pas inclure l’appariement nucléaire par exemple. Il est donc nécessaire de persévérer dans la modélisation de la dynamique des systèmes à N-corps quantiques. Notre espoir se place dans le développement de théories allant au delà de l’approximation de champ moyen. Un des buts est de pouvoir traiter correctement l’effet tunnel par lequel la fusion sous la barrière peut avoir lieu. Dans ces théories, l’état du système n’est plus limité à un simple produit antisymétrique de fonctions d’ondes à une particule (cas d’un système de particules indépendantes), encore appelé « déterminant de Slater ». La fonction d’onde à N-corps doit en effet inclure des corrélations entre les nucléons, ce qui, en pratique, peut se faire en considérant une somme de déterminants de Slater. Nous développons actuellement un modèle de mélange dynamique de configurations, fortement inspiré par la méthode des coordonnées génératrices utilisée en structure nucléaire. Nous travaillons aussi sur l’inclusion de l’appariement nucléaire dans TDHF (thèse de Benoît Avez au Service de Physique Nucléaire de Saclay).
TDHF.doc (242 Ko)
animation_74_44MeV.gif (380 Ko)
animation_74_45MeV.gif (376 Ko)
Toute une zoologie de réactions entre en compétition lors d’une collision de noyaux à basse énergie: fusion, transfert de nucléon, excitation Coulombienne et nucléaire, cassure d’un noyau en plusieurs fragments... Il n’est pas rare qu’un des partenaires de collision ait une forme très éloignée de notre image classique de goutte liquide sphérique ou faiblement déformée. C’est d’ailleurs souvent le cas pour des noyaux exotiques. Par exemple, le noyau peut avoir un halo ou une peau de neutrons. Il peut aussi être constitué d’amas de nucléons, ou encore avoir une forme de banane ou de poire prononcée.
Développer une théorie capable de traiter de manière consistante l’ensemble de ces réactions en même temps que la variété des structures possibles constitue un défi en soi. Elle serait l’illustration d’une compréhension fine des phénomènes physiques à l’échelle du noyau. De plus, une telle théorie servirait de support aux expérimentateurs, tant pour reproduire les données et aider à leur interprétation, que pour prédire des taux de production de noyaux appartenant à la terra incognita nucléaire.
Des progrès considérables ont été réalisés depuis ces trente dernières années grâce, bien sûr, aux développements d’ordinateurs puissants, mais surtout à la persévérance de physiciens talentueux comme Paul Bonche qui a passé la plus grande partie de sa carrière au Service de Physique Théorique de Saclay. Précurseur dans l’application de théories microscopiques aux collisions nucléaires, il n’a cessé de développer et d’améliorer ces modèles pour atteindre un niveau de description réaliste tant de la structure nucléaire que des mécanismes de réaction.
Son code dynamique microscopique le plus évolué utilise la théorie Hartree-Fock dépendant du temps (TDHF) en trois dimensions. Il s’agit d’une théorie de champ moyen quantique où chaque fonction d’onde (associée à un nucléon) évolue dans un champ moyen généré par l’ensemble des nucléons. Celui-ci est déterminé à l’aide d’une interaction effective de Skyrme, de portée nulle mais non-locale. Les seuls ingrédients phénoménologiques du modèle sont les paramètres de cette force. Ceux-ci, au nombre de 10, sont ajustés pour reproduire la matière nucléaire infinie et des propriétés statiques d’un petit nombre de noyaux. Aucune quantité provenant de réactions n’entre en compte dans cet ajustement.
Un travail de test et d’optimisation de ce code pour l’adapter au centre ce calcul scientifique de Bruyères-le-Châtel a été effectué dernièrement avec une attention particulière aux conservations de symétries fondamentales telles que l’invariance Galiléenne et l’invariance par translation. Nous avons poursuivi le développement du code pour pouvoir traiter correctement les excitations Coulombiennes de longues portées, dont l’effet sur la fusion autour de la barrière peut s’avérer crucial. Il a aussi été modifié pour pouvoir utiliser l’état de l’art des forces de Skyrme développées par nos collaborateurs de l’IPN-Lyon, visiteurs fréquents de l’Espace de Structure Nucléaire Théorique (ESNT) à Saclay.
Les animations représentent la densité de nucléons dans le cas de deux collisions 16O+208Pb (voir aussi les figures) : l’une à une énergie de centre de masse de 74.44 MeV, juste en dessous de la barrière de fusion, et l’autre à 74.45 MeV, juste au dessus. Dans le premier cas, le système “hésite” à fusionner. Il forme un système di-nucléaire pendant un temps relativement long à l’échelle de la collision, durant lequel de la matière est échangée d’un noyau à l’autre. Puis la répulsion Coulombienne l’emporte et le système se sépare en deux fragments. Dans le deuxième cas, le système franchit la barrière de fusion grâce aux 10 keV supplémentaires pour former un noyau plus lourd. Ces calculs prédisent donc une barrière de fusion entre 74.44 et 74.45 MeV. Expérimentalement, celle-ci se distribue autour de 74 MeV, avec une largeur à mi-hauteur de 4 MeV. Il est donc frappant d’obtenir un tel accord entre l’expérience et une théorie dans laquelle, rappelons-le, aucun ajustement sur des mécanismes de réaction n’est effectué. Le même accord a été obtenu pour différents systèmes mesurés expérimentalement, avec des partenaires de masses et de formes variées. Enfin, les animations illustrent la richesse des phénomènes physiques décrits par TDHF: la diffusivité des surfaces nucléaires, la formation d’un col au commencement de la fusion, la forme octupolaire du système composé...
L’achèvement de ce code va donc permettre des études systématiques des mécanismes de réactions tels que ceux qui seront étudiés à SPIRAL2. Cependant le modèle a ses limites, comme de ne pouvoir traiter la fusion sous-Coulombienne ou de ne pas inclure l’appariement nucléaire par exemple. Il est donc nécessaire de persévérer dans la modélisation de la dynamique des systèmes à N-corps quantiques. Notre espoir se place dans le développement de théories allant au delà de l’approximation de champ moyen. Un des buts est de pouvoir traiter correctement l’effet tunnel par lequel la fusion sous la barrière peut avoir lieu. Dans ces théories, l’état du système n’est plus limité à un simple produit antisymétrique de fonctions d’ondes à une particule (cas d’un système de particules indépendantes), encore appelé « déterminant de Slater ». La fonction d’onde à N-corps doit en effet inclure des corrélations entre les nucléons, ce qui, en pratique, peut se faire en considérant une somme de déterminants de Slater. Nous développons actuellement un modèle de mélange dynamique de configurations, fortement inspiré par la méthode des coordonnées génératrices utilisée en structure nucléaire. Nous travaillons aussi sur l’inclusion de l’appariement nucléaire dans TDHF (thèse de Benoît Avez au Service de Physique Nucléaire de Saclay).
TDHF.doc (242 Ko)
animation_74_44MeV.gif (380 Ko)
animation_74_45MeV.gif (376 Ko)

