SYSTEMS FOR JAZZ GUITAR
1. PRELIMINARY REMINDERS
1.1. Time and Key Signatures
1.1.1. Keys


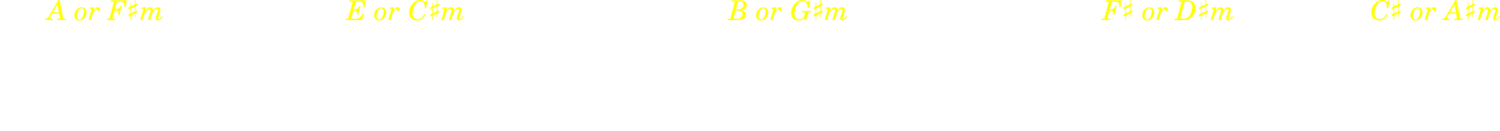

1.1.2. Tempo ranges
| Jazz tempo | Classical tempo | BPM |
|---|---|---|
| Very fast | … | > 290 |
| Up tempo, fast | … | 230 - 290 |
| Medium-up tempo, medium fast | prestissimo | 180 - 230 |
| Medium tempo, moderate | allegro | 120 - 180 |
| Walking tempo | moderato | 100 - 120 |
| Slow swing | andante | 80 - 100 |
| Medium ballad | adagio | 60 - 80 |
| Slow ballad | largo | 40 - 60 |
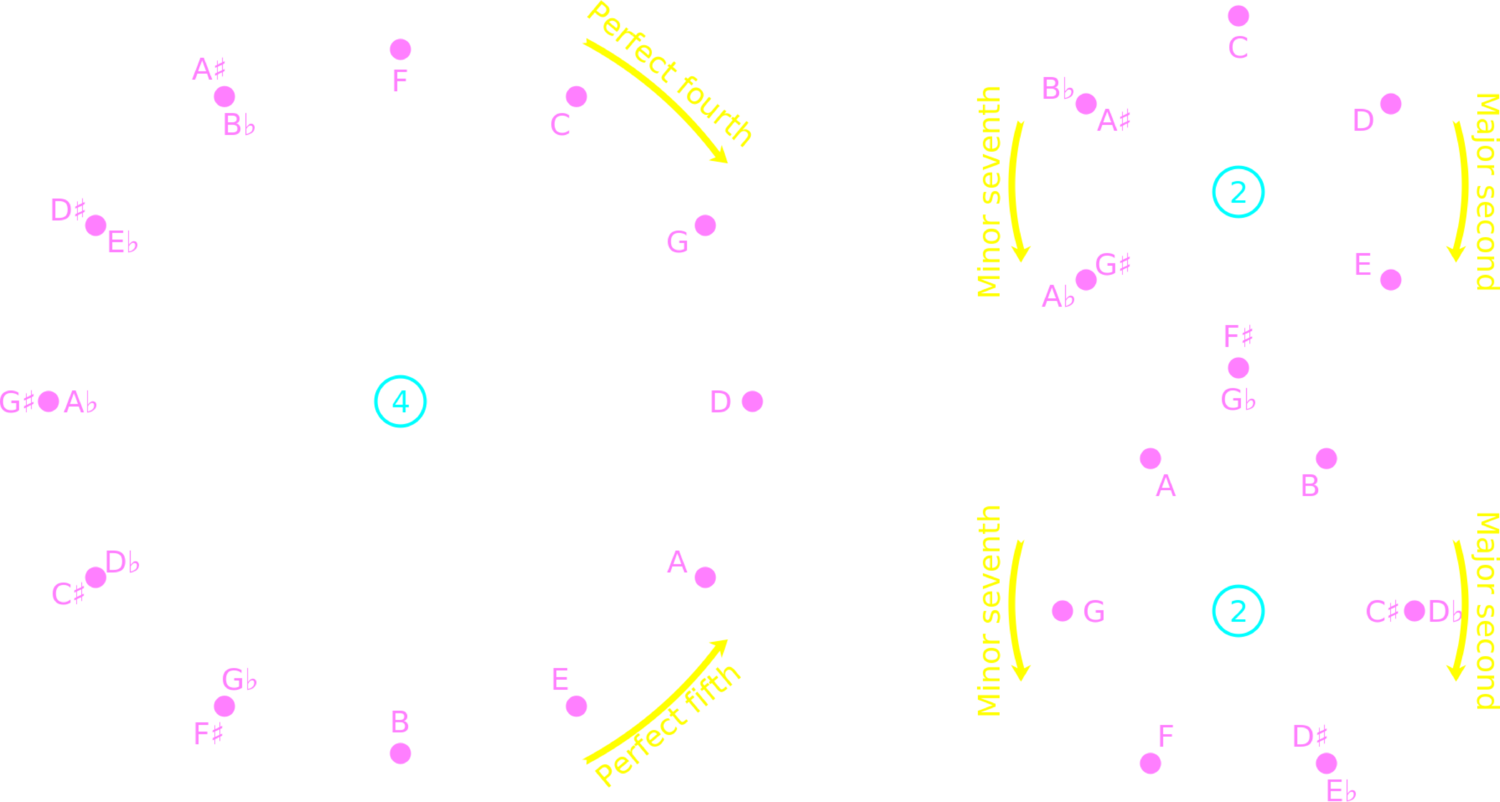
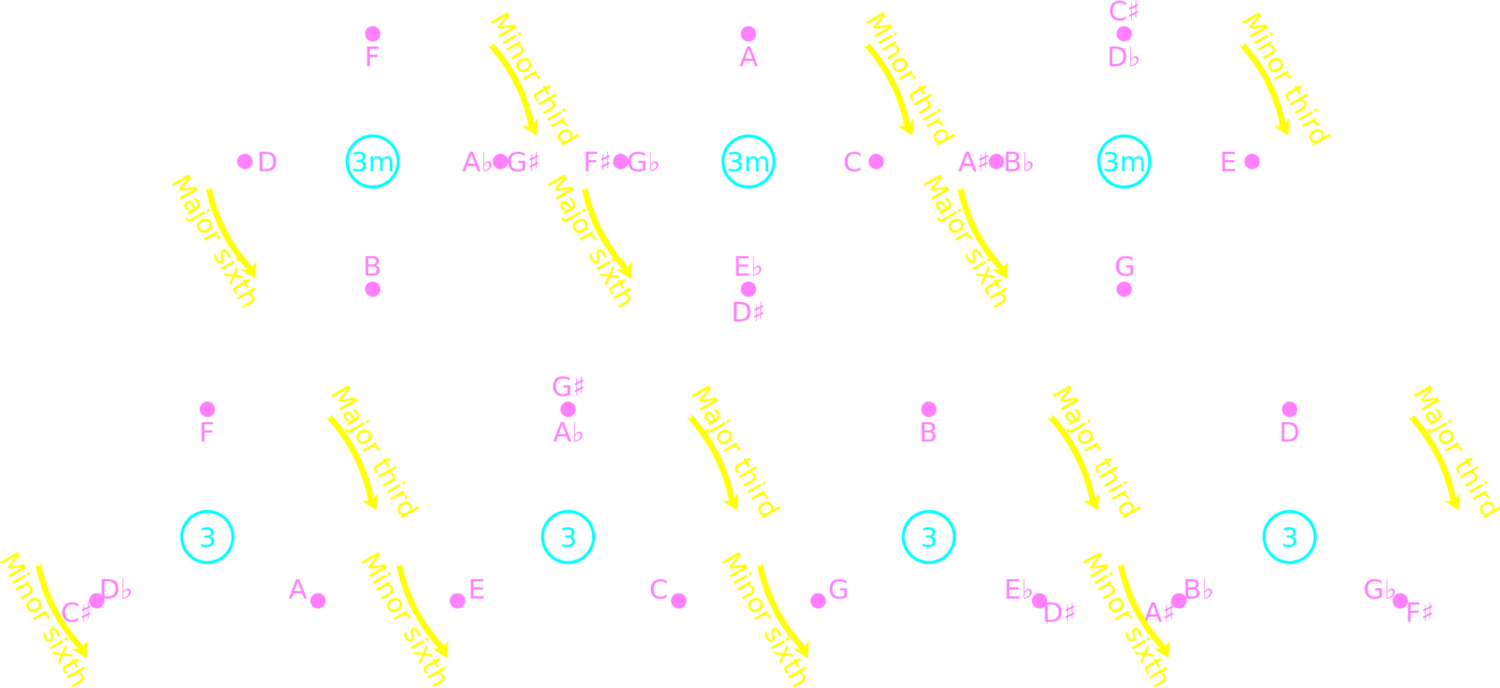
1.2. Interval Cycles
2. UNIQUE MELODIC ELEMENTS
2.1. Triads
The four triads formed by combining major and minor thirds are the following. The most useful way to play them are:
- in the five CAGED positions;
- in the six two-and-one-notes-per-string positions.

The two most useful harmonizations, easy to play on the guitar, are the following. The compact forms can be played on adjacent string groups. The drop-2 forms have one or two string skips, depending on the inversion and on the quality of the chord.

2.2. Sevenths Chords
There are seven four-note arpeggios obtained by combining major and minor thirds, the eighth one being only the augmented triad with the root repeated one octave higher. The most useful way to play them are:
- in the five CAGED positions;
- in the four two-notes-per-string positions (go well with slurring);
- in the eight three-and-one-notes-per-string positions (go well with economy picking).




These arpeggios can be arranged in different chord forms.
- The compact form can be played on the guitar mostly in its fundamental inversion. The other inversions are playable only in the higher register, using open strings, or with a non-standard tuning such as Frank GAMBALE's.
- Drop-2 forms can be played on adjacent string groups (there are thus three unisons of each chord on the guitar neck).
- Drop-3 forms can be played with a detached bass (thus two unisons per chord).
- Drop-2,3 forms can be played with a string skip in the middle (thus two unisons per chord).
- Drop-2,4 forms can be played with a detached high note (thus two unisons per chord).
- Drop-2,3,4 forms can be played with the bass on the low E string and the three other notes on the three high strings (thus only one unison per chord).



In addition, two categories of incomplete chords can be very practical.
- Shell voicings, are efficient for staccato punctuation or quarter note comping. They sound a bit lacking when held for a long time.
- Octave chords have a repeated note:
- Regular octave chords can be played on the same string groups as Drop-2;
- Double octave chords can be played on the low E, D, G and high E strings.


2.3. Pentatonic Scales
The most common pentatonic scales for improvising are the following. We also give the name of the relative minor for the first three.
- The most useful positions are two notes per string.
- They can also be played in the fifteen positions with three and two notes per strings.






2.4. Blues Scales
The blues scales can be played as a pentatonic plus the blue note. It can also be played three notes per strings (good for economy picking).

2.5. Heptatonic Scales
There are seven positions to play these scales, three notes per strings. They are the most useful both for economy picking and slurring.





2.6. Symmetric Scales



3. GENERALIZATION OF THE CONCEPT OF MODE
Here, we go through all the combinations of a unique melodic element played against an arbitrary bass note. Not all are interesting, but we still list them for completeness.
3.1. Triads
3.1.1. Major
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(/\mathrm{C}\) | 1 | 3 | 5 | C\(^\Delta\), C\(^7\) | |||||||||
| B\(/\mathrm{C}\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 7 | … | |||||||||
| B\(\flat/\mathrm{C}\) | 9 | 4/11 | \(\flat7\) | Cm\(^7\), C\(^{7sus}\) | |||||||||
| A\(/\mathrm{C}\) | \(\flat9\) | 3 | 13 | C\(^{7alt}\) | |||||||||
| A\(\flat/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | \(\sharp5/\flat13\) | C\(^{7alt}\) | |||||||||
| G\(/\mathrm{C}\) | 9 | 5 | 7 | C\(^\Delta\), Cm\(^{\Delta}\) | |||||||||
| F\(\sharp/\mathrm{C}\) | \(\flat9\) | \(\flat5/\sharp11\) | \(\flat7\) | C\(^{7alt}\) | |||||||||
| F\(/\mathrm{C}\) | 1 | 4/11 | 13 | C\(^{sus}\), Cm\(^{\Delta}\), Cm\(^7\) | |||||||||
| E\(/\mathrm{C}\) | 3 | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | |||||||||
| E\(\flat/\mathrm{C}\) | 3m/\(\sharp9\) | 5 | \(\flat7\) | Cm7, C\(^{7alt}\) | |||||||||
| D\(/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | 13 | C\(^\Delta\), C\(^7\) | |||||||||
| C\(\sharp/\mathrm{C}\) | \(\flat9\) | 4/11 | \(\sharp5/\flat13\) | … |
3.1.2. Minor
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cm\(/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 5 | Cm\(^\Delta\), Cm\(^7\) | |||||||||
| Bm\(/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | 7 | C\(^\Delta\) | |||||||||
| B\(\flat\mathrm{m}/\mathrm{C}\) | \(\flat9\) | 4/11 | \(\flat7\) | C\(^{7\flat9sus}\) | |||||||||
| Am\(/\mathrm{C}\) | 1 | 3 | 13 | C\(^\Delta\), C\(^{7}\) | |||||||||
| A\(\flat\mathrm{m}/\mathrm{C}\) | 3m/\(\sharp9\) | \(\sharp5/\flat13\) | 7 | … | |||||||||
| Gm\(/\mathrm{C}\) | 9 | 5 | \(\flat7\) | C\(^\Delta\), Cm\(^{\Delta}\), C\(^7\) | |||||||||
| F\(\sharp\mathrm{m}/\mathrm{C}\) | \(\flat9\) | \(\flat5/\sharp11\) | 13 | C\(^{7alt}\) | |||||||||
| Fm\(/\mathrm{C}\) | 1 | 4/11 | \(\sharp5/\flat13\) | … | |||||||||
| Em\(/\mathrm{C}\) | 3 | 5 | 7 | C\(^{\Delta}\) | |||||||||
| E\(\flat\mathrm{m}/\mathrm{C}\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\), C\(^{7alt}\) | |||||||||
| Dm\(/\mathrm{C}\) | 9 | 4/11 | 13 | C\(^{7sus}\), Cm\(^7\) | |||||||||
| C\(\sharp\mathrm{m}/\mathrm{C}\) | \(\flat9\) | 3 | \(\sharp5/\flat13\) | C\(^{7alt}\) |
3.1.3. Diminished
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(^{\circ}/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | C\(^{\circ7}\), C\(^\varnothing\), C\(^{7alt}\) | |||||||||
| B\(^\circ/\mathrm{C}\) | 9 | 4/11 | 7 | … | |||||||||
| B\(\flat^\circ/\mathrm{C}\) | \(\flat9\) | 3 | \(\flat7\) | C\(^{7alt}\) | |||||||||
| A\(^\circ/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 13 | Cm\(^\Delta\), Cm\(^{7}\) | |||||||||
| A\(\flat^\circ/\mathrm{C}\) | 9 | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | |||||||||
| G\(^\circ/\mathrm{C}\) | \(\flat9\) | 5 | \(\flat7\) | C\(^{7alt}\) | |||||||||
| F\(\sharp^\circ/\mathrm{C}\) | 1 | \(\flat5/\sharp11\) | 13 | C\(^\Delta\), C\(^{7}\), C\(^\varnothing\) | |||||||||
| F\(^\circ/\mathrm{C}\) | 4/11 | \(\sharp5/\flat13\) | 7 | ||||||||||
| E\(^\circ/\mathrm{C}\) | 3 | 5 | \(\flat7\) | C\(^7\) | |||||||||
| E\(\flat^\circ/\mathrm{C}\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 13 | C\(^\varnothing\), C\(^{7alt}\) | |||||||||
| D\(^\circ/\mathrm{C}\) | 9 | 4/11 | \(\sharp5/\flat13\) | … | |||||||||
| C\(\sharp^\circ/\mathrm{C}\) | \(\flat9\) | 3 | 5 | C\(^{7alt}\) |
3.1.4. Augmented
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(+/\mathrm{C}\), E\(+/\mathrm{C}\), A\(\flat+/\mathrm{C}\) | 1 | 3 | \(\sharp5/\flat13\) | C\(^{\Delta\sharp5}\), C\(^{7alt}\) | |||||||||
| B\(+/\mathrm{C}\), E\(\flat+/\mathrm{C}\), G\(+/\mathrm{C}\) | 3m/\(\sharp9\) | 5 | 7 | Cm\(^\Delta\) | |||||||||
| B\(\flat+/\mathrm{C}\), D\(+/\mathrm{C}\), F\(\sharp+/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^{7}\) | |||||||||
| A\(+/\mathrm{C}\), C\(\sharp+/\mathrm{C}\), F\(+/\mathrm{C}\) | \(\flat9\) | 4/11 | 13 | … |
3.2. Seventh Arpeggios
3.2.1. Major seventh
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(^\Delta/\mathrm{C}\) | 1 | 3 | 5 | 7 | C\(^\Delta\) | ||||||||
| B\(^\Delta/\mathrm{C}\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\flat7\) | 7 | … | ||||||||
| B\(\flat^{\Delta}/\mathrm{C}\) | 9 | 4/11 | 13 | \(\flat7\) | Cm\(^7\), C\(^{7sus}\) | ||||||||
| A\(^\Delta/\mathrm{C}\) | \(\flat9\) | 3 | \(\sharp5/\flat13\) | 13 | C\(^{7alt}\) | ||||||||
| A\(\flat^{\Delta}/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 5 | \(\sharp5/\flat13\) | C\(^{7alt}\) | ||||||||
| G\(^\Delta/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | 5 | 7 | C\(^\Delta\), Cm\(^{\Delta}\) | ||||||||
| F\(\sharp^{\Delta}/\mathrm{C}\) | \(\flat9\) | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\) | ||||||||
| F\(^\Delta/\mathrm{C}\) | 1 | 3 | 4/11 | 13 | C\(^{sus}\) | ||||||||
| E\(^\Delta/\mathrm{C}\) | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | ||||||||
| E\(\flat^\Delta/\mathrm{C}\) | 9 | 3m/\(\sharp9\) | 5 | \(\flat7\) | Cm7 | ||||||||
| D\(^\Delta/\mathrm{C}\) | \(\flat9\) | 9 | \(\flat5/\sharp11\) | 13 | … | ||||||||
| C\(\sharp^\Delta/\mathrm{C}\) | 1 | \(\flat9\) | 4/11 | \(\sharp5/\flat13\) | … |
3.2.2. Minor major seventh
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cm\(^\Delta/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 5 | 7 | Cm\(^\Delta\) | ||||||||
| Bm\(^\Delta/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | \(\flat7\) | 7 | … | ||||||||
| B\(\flat\textrm{m}^{\Delta}/\mathrm{C}\) | \(\flat9\) | 4/11 | 13 | \(\flat7\) | C\(^{7\flat9sus}\) | ||||||||
| Am\(^\Delta/\mathrm{C}\) | 1 | 3 | \(\sharp5/\flat13\) | 13 | C\(^{\Delta\sharp5}\) | ||||||||
| A\(\flat\textrm{m}^{\Delta}/\mathrm{C}\) | 3m/\(\sharp9\) | 5 | \(\sharp5/\flat13\) | 7 | … | ||||||||
| Gm\(^\Delta/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | C\(^7\) | ||||||||
| F\(\sharp\textrm{m}^{\Delta}/\mathrm{C}\) | \(\flat9\) | 4/11 | \(\flat5/\sharp11\) | 13 | C\(^{\circ7}\) | ||||||||
| Fm\(^\Delta/\mathrm{C}\) | 1 | 3 | 4/11 | \(\sharp5/\flat13\) | … | ||||||||
| Em\(^\Delta/\mathrm{C}\) | 3m/\(\sharp9\) | 3 | 5 | 7 | C\(^{\Delta}\) | ||||||||
| E\(\flat\textrm{m}^\Delta/\mathrm{C}\) | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\flat7\) | C\(^{\varnothing}\) | ||||||||
| Dm\(^\Delta/\mathrm{C}\) | \(\flat9\) | 9 | 4/11 | 13 | … | ||||||||
| C\(\sharp\textrm{m}^\Delta/\mathrm{C}\) | 1 | \(\flat9\) | 3 | \(\sharp5/\flat13\) | C\(^{7alt}\) |
3.2.3. Dominant seventh
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(^7/\mathrm{C}\) | 1 | 3 | 5 | \(\flat7\) | C\(^7\) | ||||||||
| B\(^7/\mathrm{C}\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 13 | 7 | … | ||||||||
| B\(\flat^{7}/\mathrm{C}\) | 9 | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | … | ||||||||
| A\(^7/\mathrm{C}\) | \(\flat9\) | 3 | 5 | 13 | C\(^{7alt}\) | ||||||||
| A\(\flat^{7}/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | C\(^{7alt}\) | ||||||||
| G\(^7/\mathrm{C}\) | 9 | 4/11 | 5 | 7 | … | ||||||||
| F\(\sharp^{7}/\mathrm{C}\) | \(\flat9\) | 3 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^{7alt}\) | ||||||||
| F\(^7/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 4/11 | 13 | Cm\(^{7}\), Cm\(^\Delta\) | ||||||||
| E\(^7/\mathrm{C}\) | 9 | 3 | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | ||||||||
| E\(\flat^7/\mathrm{C}\) | \(\flat9\) | 3m/\(\sharp9\) | 5 | \(\flat7\) | C\(^{7alt}\) | ||||||||
| D\(^7/\mathrm{C}\) | 1 | 9 | \(\flat5/\sharp11\) | 13 | C\(^\Delta\), C\(^7\) | ||||||||
| C\(\sharp^7/\mathrm{C}\) | \(\flat9\) | 4/11 | \(\sharp5/\flat13\) | 7 | … |
3.2.4. Minor seventh
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cm\(^7/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 5 | \(\flat7\) | Cm\(^7\) | ||||||||
| Bm\(^7/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | 13 | 7 | C\(^\Delta\) | ||||||||
| B\(\flat\mathrm{m}^{7}/\mathrm{C}\) | \(\flat9\) | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | … | ||||||||
| Am\(^7/\mathrm{C}\) | 1 | 3 | 5 | 13 | C\(^\Delta\), C\(^{7}\) | ||||||||
| A\(\flat\mathrm{m}^{7}/\mathrm{C}\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | … | ||||||||
| Gm\(^7/\mathrm{C}\) | 9 | 4/11 | 5 | \(\flat7\) | Cm\(^7\) | ||||||||
| F\(\sharp\mathrm{m}^{7}/\mathrm{C}\) | \(\flat9\) | 3 | \(\flat5/\sharp11\) | 13 | C\(^{7alt}\) | ||||||||
| Fm\(^7/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | … | ||||||||
| Em\(^7/\mathrm{C}\) | 9 | 3 | 5 | 7 | C\(^{\Delta}\) | ||||||||
| E\(\flat\mathrm{m}^7/\mathrm{C}\) | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\flat7\) | C\(^{7alt}\) | ||||||||
| Dm\(^7/\mathrm{C}\) | 1 | 9 | 4/11 | 13 | C\(^{7sus}\), Cm\(^7\) | ||||||||
| C\(\sharp\mathrm{m}^7/\mathrm{C}\) | \(\flat9\) | 3 | \(\sharp5/\flat13\) | 7 | … |
3.2.5. Half-diminished
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(^\varnothing/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\) | ||||||||
| B\(^\varnothing/\mathrm{C}\) | 9 | 4/11 | 13 | 7 | … | ||||||||
| B\(\flat^{\varnothing}\mathrm{C}\) | \(\flat9\) | 3 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | ||||||||
| A\(^\varnothing/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 5 | 13 | Cm\(^\Delta\), Cm\(^{7}\) | ||||||||
| A\(\flat^{\varnothing}/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | ||||||||
| G\(^\varnothing/\mathrm{C}\) | \(\flat9\) | 4/11 | 5 | \(\flat7\) | C\(^{7\flat9sus}\) | ||||||||
| F\(\sharp^{\varnothing}/\mathrm{C}\) | 1 | 3 | \(\flat5/\sharp11\) | 13 | C\(^\Delta\), C\(^7\) | ||||||||
| F\(^\varnothing/\mathrm{C}\) | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | 7 | … | ||||||||
| E\(^\varnothing/\mathrm{C}\) | 9 | 3 | 5 | \(\flat7\) | C\(^7\) | ||||||||
| E\(\flat^\varnothing/\mathrm{C}\) | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 13 | C\(^{7alt}\) | ||||||||
| D\(^\varnothing/\mathrm{C}\) | 1 | 9 | 4/11 | \(\sharp5/\flat13\) | … | ||||||||
| C\(\sharp^\varnothing/\mathrm{C}\) | \(\flat9\) | 3 | 5 | 7 | … |
3.2.6. Diminished
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(^{\circ7}/\mathrm{C}\), A\(^{\circ7}/\textrm{C}\), F\(\sharp^{\circ7}/\textrm{C}\), E\(\flat^{\circ7}/\textrm{C}\) | 1 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 13 | C\(^{\circ7}\) | ||||||||
| B\(^{\circ7}/\mathrm{C}\), A\(\flat^{\circ7}/\textrm{C}\), F\(^{\circ7}/\textrm{C}\), D\(^{\circ7}/\textrm{C}\) | 9 | 4/11 | \(\sharp5/\flat13\) | 7 | … | ||||||||
| B\(\flat^{\circ7}/\mathrm{C}\), G\(^{\circ7}/\textrm{C}\), E\(^{\circ7}/\textrm{C}\), C\(\sharp^{\circ7}/\textrm{C}\) | \(\flat9\) | 3 | 5 | \(\flat7\) | C\(^{7alt}\) |
3.2.7. Major seventh augmented
| Substitution | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C\(^{\Delta\sharp5}/\mathrm{C}\) | 1 | 3 | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | ||||||||
| B\(^{\Delta\sharp5}/\mathrm{C}\) | 3m/\(\sharp9\) | 5 | \(\flat7\) | 7 | … | ||||||||
| B\(\flat^{\Delta\sharp5}/\mathrm{C}\) | 9 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^7\) | ||||||||
| A\(^{\Delta\sharp5}/\mathrm{C}\) | \(\flat9\) | 4/11 | \(\sharp5/\flat13\) | 13 | … | ||||||||
| A\(\flat^{\Delta\sharp5}/\mathrm{C}\) | 1 | 3 | 5 | \(\sharp5/\flat13\) | C\(^{7alt}\) | ||||||||
| G\(^{\Delta\sharp5}/\mathrm{C}\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | 7 | … | ||||||||
| F\(\sharp^{\Delta\sharp5}/\mathrm{C}\) | 9 | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\) | ||||||||
| F\(^{\Delta\sharp5}/\mathrm{C}\) | \(\flat9\) | 3 | 4/11 | 13 | … | ||||||||
| E\(^{\Delta\sharp5}/\mathrm{C}\) | 1 | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | C\(^{7alt}\) | ||||||||
| E\(\flat^{\Delta\sharp5}/\mathrm{C}\) | 9 | 3m/\(\sharp9\) | 5 | 7 | Cm\(^\Delta\) | ||||||||
| D\(^{\Delta\sharp5}/\mathrm{C}\) | \(\flat9\) | 9 | \(\flat5/\sharp11\) | \(\flat7\) | … | ||||||||
| C\(\sharp^{\Delta\sharp5}/\mathrm{C}\) | 1 | \(\flat9\) | 4/11 | 13 | C\(^{7\flat9sus}\) |
3.3. Pentatonics (⬟)
3.3.1. Major ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 9 | 3 | 5 | 13 | C\(^{\Delta}\), C\(^7\) | Natural ⬟ | |||||||
| B ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 1 | 9 | 4/11 | 5 | \(\flat7\) | Cm\(^7\), C\(^{7sus}\) | Egyptian ⬟ | |||||||
| A ⬟/C | \(\flat9\) | 3 | \(\flat5/\sharp11\) | 13 | 7 | … | … | |||||||
| A\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | … | … | |||||||
| G ⬟/C | 9 | 3 | 5 | 13 | 7 | C\(^\Delta\) | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| F ⬟/C | 1 | 9 | 4/11 | 5 | 13 | Cm, C\(^{7sus}\) | … | |||||||
| E ⬟/C | \(\flat9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | … | … | |||||||
| E\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | 4/11 | 5 | \(\flat7\) | Cm\(^7\) | Minor ⬟ | |||||||
| D ⬟/C | 9 | 3 | \(\flat5/\sharp11\) | 13 | 7 | C\(^\Delta\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | … | … |
3.3.2. Kumoi ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 9 | 3m/\(\sharp9\) | 5 | 13 | C, Cm | B.B. King ⬟ | |||||||
| B ⬟/C | \(\flat9\) | 9 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 1 | \(\flat9\) | 4/11 | 5 | \(\flat7\) | C\(^{7\flat9sus}\) | Kokin joshi ⬟ | |||||||
| A ⬟/C | 1 | 3 | \(\flat5/\sharp11\) | 13 | 7 | C\(^\Delta\) | Nippon ⬟ | |||||||
| A\(\flat\) ⬟/C | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||||
| G ⬟/C | 9 | 3 | 5 | 13 | \(\flat7\) | C\(^7\) | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | … | … | |||||||
| F ⬟/C | 1 | 9 | 4/11 | 5 | \(\sharp5/\flat13\) | Cm\(^7\) | Asian ⬟ | |||||||
| E ⬟/C | \(\flat9\) | 3 | \(\flat5/\sharp11\) | 5 | 7 | … | … | |||||||
| E\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\), C\(^{7alt}\) | Locrian ⬟ | |||||||
| D ⬟/C | 9 | 3 | 4/11 | 13 | 7 | C\(^\Delta\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … |
3.3.3. Dominant ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 9 | 3 | 5 | \(\flat7\) | C\(^7\) | … | |||||||
| B ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 13 | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 1 | 9 | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | … | … | |||||||
| A ⬟/C | \(\flat9\) | 3 | 5 | 13 | 7 | … | … | |||||||
| A\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^\varnothing\), C7alt$ | … | |||||||
| G ⬟/C | 9 | 4/11 | 5 | 13 | 7 | … | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| F ⬟/C | 1 | 3m/\(\sharp9\) | 4/11 | 5 | 13 | Cm\(^7\), Cm\(^\Delta\) | Dorian ⬟ | |||||||
| E ⬟/C | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | … | |||||||
| E\(\flat\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | \(\flat7\) | … | … | |||||||
| D ⬟/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | 13 | C\(^\Delta\), C\(^7\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | 7 | … | … |
3.3.4. Harmonic major ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 9 | 3 | 5 | \(\sharp5/\flat13\) | C\(^{\Delta}\), C\(^{7alt}\) | … | |||||||
| B ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 1 | 9 | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\) | … | |||||||
| A ⬟/C | \(\flat9\) | 3 | 4/11 | 13 | 7 | … | … | |||||||
| A\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| G ⬟/C | 9 | 3m/\(\sharp9\) | 5 | 13 | 7 | Cm\(^\Delta\) | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 9 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| F ⬟/C | 1 | \(\flat9\) | 4/11 | 5 | 13 | C\(^{7\flat9sus}\) | … | |||||||
| E ⬟/C | 1 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | … | |||||||
| E\(\flat\) ⬟/C | 3m/\(\sharp9\) | 4/11 | 5 | \(\flat7\) | 7 | … | … | |||||||
| D ⬟/C | 9 | 3 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^{7}\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | 13 | … | … |
3.3.5. Unitonic ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | C\(^{7alt}\), C\(^{\Delta\sharp5}\) | … | |||||||
| B ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^7\) | … | |||||||
| A ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 13 | 7 | … | … | |||||||
| A\(\flat\) ⬟/C | 1 | 9 | 3 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| G ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 5 | 13 | 7 | … | … | |||||||
| F\(\sharp\) ⬟/C | 1 | 9 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| F ⬟/C | \(\flat9\) | 4/11 | 5 | 13 | 7 | … | … | |||||||
| E ⬟/C | 1 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| E\(\flat\) ⬟/C | 3m/\(\sharp9\) | 4/11 | 5 | 13 | 7 | … | … | |||||||
| D ⬟/C | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | 13 | … | … |
3.3.6. Javanese ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 5 | 13 | C\(^{7alt}\), Cm | … | |||||||
| B ⬟/C | 1 | 9 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | C\(^{\Delta\sharp5}\) | … | |||||||
| B\(\flat\) ⬟/C | \(\flat9\) | 4/11 | 5 | \(\flat7\) | 7 | … | … | |||||||
| A ⬟/C | 1 | 3 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^7\) | … | |||||||
| A\(\flat\) ⬟/C | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||||
| G ⬟/C | 9 | 3 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | 13 | C\(^{7alt}\) | … | |||||||
| F ⬟/C | 1 | 9 | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | C\(^\varnothing\) | … | |||||||
| E ⬟/C | \(\flat9\) | 3 | 4/11 | 5 | 7 | … | … | |||||||
| E\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^7\), C\(^{7alt}\) | … | |||||||
| D ⬟/C | 9 | 3m/\(\sharp9\) | 4/11 | 13 | 7 | Cm\(^\Delta\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 9 | 3 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … |
3.3.7. Diminished ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 13 | C\(^{\circ7}\), C\(^\varnothing\) | … | |||||||
| B ⬟/C | \(\flat9\) | 9 | 4/11 | \(\sharp5/\flat13\) | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 1 | \(\flat9\) | 3 | 5 | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| A ⬟/C | 1 | 3m\(\sharp9\) | \(\flat5/\sharp11\) | 13 | 7 | C\(^{\circ7}\) | … | |||||||
| A\(\flat\) ⬟/C | 9 | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||||
| G ⬟/C | \(\flat9\) | 3 | 5 | 13 | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| F\(\sharp\) ⬟/C | 1 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | C\(^{\circ7}\) | … | |||||||
| F ⬟/C | 9 | 4/11 | 5 | \(\sharp5/\flat13\) | 7 | … | … | |||||||
| E ⬟/C | \(\flat9\) | 3 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| E\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 13 | C\(^{\circ7}\), C\(^\varnothing\) | ||||||||
| D ⬟/C | 9 | 3 | 4/11 | \(\sharp5/\flat13\) | 7 | … | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | 5 | \(\flat7\) | C\(^{7alt}\) | … |
3.3.8. 7#9 ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 3m/\(\sharp9\) | 3 | 5 | \(\flat7\) | C\(^7\) | … | |||||||
| B ⬟/C | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 13 | 7 | C\(^\varnothing\) | … | |||||||
| B\(\flat\) ⬟/C | \(\flat9\) | 9 | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | … | … | |||||||
| A ⬟/C | 1 | \(\flat9\) | 3 | 5 | 13 | C\(^{7alt}\) | … | |||||||
| A\(\flat\) ⬟/C | 1 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | … | … | |||||||
| G ⬟/C | 9 | 4/11 | 5 | \(\flat7\) | 7 | … | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 3 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| F ⬟/C | 1 | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | 13 | … | … | |||||||
| E ⬟/C | 9 | 3 | 5 | \(\sharp5/\flat13\) | 7 | C\(^\Delta\) | … | |||||||
| E\(\flat\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| D ⬟/C | 1 | 9 | 4/11 | \(\flat5/\sharp11\) | 13 | C\(^\varnothing\) | … | |||||||
| C$\sharp ⬟/C | \(\flat9\) | 3 | 4/11 | \(\sharp5/\flat13\) | 7 | … | … |
3.3.9. Indian ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 3 | 4/11 | 5 | \(\flat7\) | C\(^7\), C\(^{7sus}\) | … | |||||||
| B ⬟/C | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 13 | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 9 | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^\varnothing\) | … | |||||||
| A ⬟/C | \(\flat9\) | 9 | 3 | 5 | 13 | … | … | |||||||
| A\(\flat\) ⬟/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | C\(^{7alt}\) | … | |||||||
| G ⬟/C | 1 | 9 | 4/11 | 5 | 7 | Cm\(^\Delta\) | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 3 | \(\flat5/\sharp13\) | \(\flat7\) | 7 | … | … | |||||||
| F ⬟/C | 1 | 3m/\(\sharp9\) | 4/11 | 13 | \(\flat7\) | Cm\(^7\)` | … | |||||||
| E ⬟/C | 9 | 3 | \(\sharp5/\flat13\) | 13 | 7 | C\(^{\Delta\sharp5}\) | … | |||||||
| E\(\flat\) ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 5 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||||
| D ⬟/C | 1 | 9 | \(\flat5/\sharp11\) | 5 | 13 | C\(^\Delta\), C\(^7\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | … | … |
3.3.10. Chinese ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 3 | \(\flat5/\sharp11\) | 5 | 7 | C\(^\Delta\) | … | |||||||
| B ⬟/C | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | 7 | … | … | |||||||
| B\(\flat\) ⬟/C | 9 | 3 | 4/11 | 13 | \(\flat7\) | C\(^{7sus}\) | … | |||||||
| A ⬟/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | 13 | C\(^{7alt}\) | … | |||||||
| A\(\flat\) ⬟/C | 1 | 9 | 3m/\(\sharp9\) | 5 | \(\sharp5/\flat13\) | Cm | Hirajoshi ⬟ | |||||||
| G ⬟/C | \(\flat9\) | 9 | \(\flat5/\sharp11\) | 5 | 7 | … | … | |||||||
| F\(\sharp\) ⬟/C | 1 | \(\flat9\) | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\) | Iwato ⬟ | |||||||
| F ⬟/C | 1 | 3 | 4/11 | 13 | 7 | C\(^\Delta\) | Japo ⬟ | |||||||
| E ⬟/C | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||||
| E\(\flat\) ⬟/C | 9 | 3m/\(\sharp9\) | 5 | 13 | \(\flat7\) | Cm\(^7\) | … | |||||||
| D ⬟/C | \(\flat9\) | 9 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | … | … | |||||||
| C\(\sharp\) ⬟/C | 1 | \(\flat9\) | 4/11 | 5 | \(\sharp5/\flat13\) | … | … |
3.3.11. Vietnamese ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | C\(^\Delta\) | … | |||||||
| B ⬟/C | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | 7 | C\(^\Delta\) | … | |||||||
| B\(\flat\) ⬟/C | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | C\(^\varnothing\) | … | |||||||
| A ⬟/C | \(\flat9\) | 9 | 3 | 4/11 | 13 | … | … | |||||||
| A\(\flat\) ⬟/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | C\(^{7alt}\) | … | |||||||
| G ⬟/C | 1 | 9 | 3m/\(\sharp9\) | 5 | 7 | Cm\(^\Delta\) | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 9 | \(\flat5/\sharp11\) | \(\flat7\) | 7 | … | … | |||||||
| F ⬟/C | 1 | \(\flat9\) | 4/11 | 13 | \(\flat7\) | C\(^{7\flat9sus}\) | … | |||||||
| E ⬟/C | 1 | 3 | \(\sharp5/\flat13\) | 13 | 7 | C\(^{\Delta\sharp5}\) | … | |||||||
| E\(\flat\) ⬟/C | 3m/\(\sharp9\) | 5 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||||
| D ⬟/C | 9 | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | C\(^7\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | … | … |
3.3.12. Balinese ⬟
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C ⬟/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 5 | \(\sharp5/\flat13\) | C\(^{7alt}\) | Pelog ⬟ | |||||||
| B ⬟/C | 1 | 9 | \(\flat5/\sharp11\) | 5 | 7 | C\(^\Delta\) | … | |||||||
| B\(\flat\) ⬟/C | \(\flat9\) | 4/11 | \(\flat5/\sharp11\) | \(\flat7\) | 7 | … | … | |||||||
| A ⬟/C | 1 | 3 | 4/11 | 13 | \(\flat7\) | C\(^7\), C\(^{7sus}\) | … | |||||||
| A\(\flat\) ⬟/C | 3m/\(\sharp9\) | 3 | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||||
| G ⬟/C | 9 | 3m/\(\sharp9\) | 5 | \(\sharp5/\flat13\) | \(\flat7\) | Cm\(^7\) | … | |||||||
| F\(\sharp\) ⬟/C | \(\flat9\) | 9 | \(\flat5/\sharp11\) | 5 | 13 | … | … | |||||||
| F ⬟/C | 1 | \(\flat9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | … | … | |||||||
| E ⬟/C | 1 | 3 | 4/11 | 5 | 7 | C\(^\Delta\) | Mauritanian ⬟ | |||||||
| E\(\flat\) ⬟/C | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\flat7\) | 7 | … | … | |||||||
| D ⬟/C | 9 | 3m/\(\sharp9\) | 4/11 | 13 | \(\flat7\) | Cm\(^7\) | … | |||||||
| C\(\sharp\) ⬟/C | \(\flat9\) | 9 | 3 | \(\sharp5/\flat13\) | 13 | … | … |
3.4. Blues Scales
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C blues/C | 1 | 9 | 3m/\(\sharp9\) | 3 | 5 | 13 | C\(^{\Delta}\), C\(^7\) | Major blues | ||||||
| B blues/C | \(\flat9\) | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | … | … | ||||||
| B\(\flat\) blues/C | 1 | \(\flat9\) | 9 | 4/11 | 5 | \(\flat7\) | … | … | ||||||
| A blues/C | 1 | \(\flat9\) | 3 | \(\flat5/\sharp11\) | 13 | 7 | … | … | ||||||
| A\(\flat\) blues/C | 1 | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | ||||||
| G blues/C | 9 | 3 | 5 | 13 | \(\flat\) | 7 | C\(^7\) | … | ||||||
| F\(\sharp\) blues/C | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | \(\flat7\) | C\(^{7alt}\) | … | ||||||
| F blues/C | 1 | 9 | 4/11 | 5 | \(\sharp5/\flat13\) | 13 | \(\flat7\) | C\(^{7sus}\) | … | |||||
| E blues/C | \(\flat9\) | 3 | \(\flat5/\sharp11\) | 5 | \(\sharp5/\flat13\) | 7 | … | … | ||||||
| E\(\flat\) blues/C | 1 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | C\(^7\), Cm\(^7\) | Minor blues | ||||||
| D blues/C | 9 | 3 | 4/11 | \(\flat5/\sharp11\) | 13 | 7 | C\(^\Delta\) | … | ||||||
| C\(\sharp\) blues/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … |
3.5. Heptatonics
3.5.1. Diatonic scale
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C diat./C | 1 | 9 | 3 | 4/11 | 5 | 13 | 7 | C\(^{\Delta}\) | Ionian | |||||
| B diat./C | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| B\(\flat\) diat./C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | 5 | 13 | \(\flat7\) | Cm\(^7\) | Dorian | |||||
| A diat./C | \(\flat9\) | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| A\(\flat\) diat./C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | Cm\(^7\) | Phrygian | |||||
| G diat./C | 1 | 9 | 3 | \(\flat5/\sharp11\) | 5 | 13 | 7 | C\(^\Delta\) | Lydian | |||||
| F\(\sharp\) diat./C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| F diat./C | 1 | 9 | 3 | 4/11 | 5 | 13 | \(\flat7\) | C\(^7\) | Mixolydian | |||||
| E diat./C | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| E\(\flat\) diat./C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | Cm\(^7\) | Aeolian | |||||
| D diat./C | \(\flat9\) | 9 | 3 | \(\flat5/\sharp11\) | 5 | 13 | 7 | … | … | |||||
| C\(\sharp\) diat./C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^\varnothing\) | Locrian |
3.5.2. Minor melodic scale (mm)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C mm/C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | 5 | 13 | 7 | Cm\(^{\Delta}\) | Minor melodic | |||||
| B mm/C | \(\flat9\) | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| B\(\flat\) mm/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | 13 | \(\flat7\) | C\(^{7\flat9sus}\) | Javanese | |||||
| A mm/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | C\(^{\Delta\sharp5}\) | Lydian augmented | |||||
| A\(\flat\) mm/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| G mm/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | C\(^7\) | Lydian dominant | |||||
| F\(\sharp\) mm/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| F mm/C | 1 | 9 | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | Aeolian dominant | |||||
| E mm/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | 13 | 7 | … | … | |||||
| E\(\flat\) mm/C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^\varnothing\) | Locrian melodic | |||||
| D mm/C | \(\flat9\) | 9 | 3 | 4/11 | 5 | 13 | 7 | … | … | |||||
| C\(\sharp\) mm/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | Superlocrian |
3.5.3. Harmonic minor scale (hm)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C hm/C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | 7 | Cm\(^{\Delta}\) | Harmonic minor | |||||
| B hm/C | \(\flat9\) | 9 | 3 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | 7 | … | … | |||||
| B\(\flat\) hm/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^\varnothing\) | Locrian harmonic | |||||
| A hm/C | 1 | 9 | 3 | 4/11 | \(\sharp5/\flat13\) | 13 | 7 | C\(^{\Delta\sharp5}\) | Ionian augmented | |||||
| A\(\flat\) hm/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| G hm/C | 1 | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | Cm\(^7\) | Romanian | |||||
| F\(\sharp\) hm/C | \(\flat9\) | 9 | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| F hm/C | 1 | \(\flat9\) | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | Phrygian dominant | |||||
| E hm/C | 1 | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | 13 | 7 | C\(^\Delta\) | Lydian harmonic | |||||
| E\(\flat\) hm/C | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| D hm/C | \(\flat9\) | 9 | 3 | 4/11 | 5 | 13 | \(\flat7\) | … | … | |||||
| C\(\sharp\) hm/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | C\(^{7alt}\) | Harmonic altered |
3.5.4. Harmonic major scale (hM)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C hM/C | 1 | 9 | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | 7 | C\(^{\Delta}\) | … | |||||
| B hM/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | 7 | … | … | |||||
| B\(\flat\) hM/C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^\varnothing\) | … | |||||
| A hM/C | \(\flat9\) | 9 | 3 | 4/11 | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| A\(\flat\) hM/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | Superphrygian | |||||
| G hM/C | 1 | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | 13 | 7 | Cm\(^\Delta\) | Lydian minor | |||||
| F hM/C | \(\flat9\) | 9 | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| F\(\sharp\) hM/C | 1 | \(\flat9\) | 3 | 4/11 | 5 | 13 | \(\flat7\) | C\(^{7alt}\) | … | |||||
| E hM/C | 1 | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | C\(^{\Delta\sharp5}\) | … | |||||
| E\(\flat\) hM/C | 9 | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| D hM/C | \(\flat9\) | 9 | 3 | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | … | … | |||||
| C\(\sharp\) hM/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | C\(^{\circ7}\) | … |
3.5.5. Hungarian dominant scale (Hd)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C Hd/C | 1 | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | C\(^7\) | … | |||||
| B Hd/C | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| B\(\flat\) Hd/C | \(\flat9\) | 9 | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | … | … | |||||
| A Hd/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | 13 | C\(^{7alt}\) | … | |||||
| A\(\flat\) Hd/C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 7 | Cm\(^\Delta\) | … | |||||
| G Hd/C | \(\flat9\) | 9 | 3 | 4/11 | 5 | \(\flat7\) | 7 | … | … | |||||
| F\(\sharp\) Hd/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^{7alt}\) | … | |||||
| F Hd/C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | \(\sharp5/\flat13\) | 13 | 7 | Cm\(^\Delta\) | … | |||||
| E Hd/C | \(\flat9\) | 9 | 3 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| E\(\flat\) Hd/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | C\(^{7alt}\) | … | |||||
| D Hd/C | 1 | 9 | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | C\(^{\circ7}\) | … | |||||
| C\(\sharp\) Hd/C | \flat9$ | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | … | … |
3.5.6. Hungarian minor scale (Hm)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C Hm/C | 1 | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | \(\sharp5/\flat13\) | 7 | Cm\(^\Delta\) | Gypsy | |||||
| B Hm/C | \(\flat9\) | 9 | 4/11 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | 7 | … | … | |||||
| B\(\flat\) Hm/C | 1 | \(\flat9\) | 3 | 4/11 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | C\(^{7alt}\) | Eastern | |||||
| A Hm/C | 1 | 3m/\(\sharp9\) | 3 | 4/11 | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| A\(\flat\) Hm/C | 9 | 3m/\(\sharp9\) | 3 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| G Hm/C | \(\flat9\) | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | … | … | |||||
| F\(\sharp\) Hm/C | 1 | \(\flat9\) | 9 | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | … | … | |||||
| F Hm/C | 1 | \(\flat9\) | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | 7 | C\(^\Delta\) | Byzantine | |||||
| E Hm/C | 1 | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | 7 | C\(^{7alt}\) | Sebastian | |||||
| E\(\flat\) Hm/C | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | 7 | … | … | |||||
| D Hm/C | \(\flat9\) | 9 | 3 | 4/11 | \(\sharp5/\flat13\) | 13 | \(\flat7\) | … | … | |||||
| C\(\sharp\) Hm/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | 5 | \(\sharp5/\flat13\) | 13 | C\(^{7alt}\) | … |
3.5.7. Neapolitan scale (n)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C n/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | 13 | 7 | Cm\(^\Delta\) | … | |||||
| B n/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| B\(\flat\) n/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | 13 | \(\flat7\) | 7 | … | … | |||||
| A n/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | \(\flat7\) | C\(^{7alt}\) | … | |||||
| A\(\flat\) n/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| G n/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | 5 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | Arabic | |||||
| F\(\sharp\) n/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 5 | 13 | 7 | … | … | |||||
| F n/C | 1 | 9 | 3 | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||
| E n/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | 4/11 | 5 | 13 | 7 | … | … | |||||
| E\(\flat\) n/C | 1 | 9 | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||
| D n/C | \(\flat9\) | 9 | 3m/\(\sharp9\) | 4/11 | 5 | 13 | 7 | … | … | |||||
| C\(\sharp\) n/C | 1 | \(\flat9\) | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … |
3.5.8. Harmonic neapolitan scale (hn)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C hn/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | 7 | Cm\(^\Delta\) | … | |||||
| B hn/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | 7 | … | … | |||||
| B\(\flat\) hn/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | 7 | … | … | |||||
| A hn/C | 1 | 9 | 3 | 4/11 | \(\sharp5/\flat13\) | 13 | \(\flat7\) | C\(^{7alt}\) | … | |||||
| A\(\flat\) hn/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | 5 | \(\sharp5/\flat13\) | 13 | 7 | … | … | |||||
| G hn/C | 1 | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | \(\sharp5/\flat13\) | \(\flat7\) | Cm\(^7\) | … | |||||
| F\(\sharp\) hn/C | \(\flat9\) | 9 | 4/11 | \(\flat5/\sharp11\) | 5 | 13 | 7 | … | … | |||||
| F hn/C | 1 | \(\flat9\) | 3 | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||
| E hn/C | 1 | 3m/\(\sharp9\) | 3 | 4/11 | 5 | 13 | 7 | C\(^\Delta\) | … | |||||
| E\(\flat\) hn/C | 9 | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | … | |||||
| D hn/C | \(\flat9\) | 9 | 3m/\(\sharp9\) | 4/11 | 5 | 13 | \(\flat7\) | … | … | |||||
| C\(\sharp\) hn/C | 1 | \(\flat9\) | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | … | … |
3.5.9. Enigmatic scale (e)
| Mode | Play over | a.k.a. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C e/C | 1 | \(\flat9\) | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | 7 | C\(^{7alt}\) | … | |||||
| B e/C | 1 | 3m/\(\sharp9\) | 4/11 | 5 | 13 | \(\flat7\) | 7 | Cm\(^7\) | … | |||||
| B\(\flat\) e/C | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | \(\flat7\) | 7 | … | … | |||||
| A e/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | \(\sharp5/\flat13\) | 13 | \(\flat7\) | … | … | |||||
| A\(\flat\) e/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | 5 | \(\sharp5/\flat13\) | 13 | C\(^\Delta\), C\(^7\) | … | |||||
| G e/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | 5 | \(\sharp5/\flat13\) | 7 | … | … | |||||
| F\(\sharp\) e/C | 1 | 9 | 3 | 4/11 | \(\flat5/\sharp11\) | 5 | \(\flat7\) | C\(^7\) | Hybrid blues | |||||
| F e/C | \(\flat9\) | 3m/\(\sharp9\) | 3 | 4/11 | \(\flat5/\sharp11\) | 13 | 7 | … | … | |||||
| E e/C | 1 | 9 | 3m/\(\sharp9\) | 3 | 4/11 | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||
| E\(\flat\) e/C | \(\flat9\) | 9 | 3m/\(\sharp9\) | 3 | 5 | 13 | 7 | … | … | |||||
| D e/C | 1 | \(\flat9\) | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | … | |||||
| C\(\sharp\) e/C | 1 | \(\flat9\) | 9 | 4/11 | 5 | 13 | 7 | … | … |
3.6. Symmetric Scales
3.6.1. Unitonic scale (u)
| Mode | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C, D, E, F\(\sharp\), A\(\flat\), B\(\flat\) u/C | 1 | 9 | 3 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | \(\flat7\) | C\(^{7alt}\) | ||||||
| B, C\(\sharp\), E\(\flat\), F, G, A u/C | \(\flat9\) | 3m/\(\sharp9\) | 4/11 | 5 | 13 | 7 | … |
3.6.2. Augmented scale (a)
| Mode | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C, A\(\flat\), E a/C | 1 | 3m/\(\sharp9\) | 3 | 5 | \(\sharp5/\flat13\) | 7 | C\(^\Delta\) | ||||||
| B, G, E\(\flat\) a/C | 9 | 3m/\(\sharp9\) | \(\flat5/\sharp11\) | 5 | \(\flat7\) | 7 | Cm | ||||||
| B\(\flat\), F\(\sharp\), D a/C | \(\flat9\) | 9 | 4/11 | \(\flat5/\sharp11\) | 13 | \(\flat7\) | … | ||||||
| A, F, C\(\sharp\) a/C | 1 | \(\flat9\) | 3 | 4/11 | \(\sharp5/\flat13\) | 13 | … |
3.6.3. Diminished scale (d)
| Mode | Play over | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C d/C | 1 | 9 | 3m/\(\sharp9\) | 4/11 | \(\flat5/\sharp11\) | \(\sharp5/\flat13\) | 13 | 7 | C\(^{\circ7}\) | ||||
| B d/C | \(\flat9\) | 9 | 3 | 4/11 | 5 | \(\sharp5/\flat13\) | \(\flat7\) | 7 | … | ||||
| B\(\flat\) d/C | 1 | \(\flat9\) | 3m/\(\sharp9\) | 3 | \(\flat5/\sharp11\) | 5 | 13 | \(\flat7\) | C\(^7\), C\(^{7alt}\) |
4. DECLINING MELODIC ELEMENTS - DEVELOPING VERSATILITY
4.1. Using the Metronome
Practicing scales and tunes, the metronome does not have to be on each beat. Sylvain LUC showed us how it could be used to develop a good time feel. Here are a few ways to use it.




4.2. Tremolo
The following patterns can be applied to any melodic element, but they sound particularly good with arpeggios.
4.2.1. By Two

4.2.2. By Three


4.2.3. By four


4.3. Melodic Patterns
The following patterns should be practiced on all melodic elements, ascending and descending. Those highlighted in grey either contain repetitions or are equivalent to intervallic patterns. They are not necessarily bad, but they sound different.
4.3.1. Groups of three



4.3.2. Groups of four










4.4. Intervallic Patterns
The following patterns should be practiced on all melodic elements, ascending and descending. When applied to arpeggios or pentatonic scales, the interval jumps are larger than what is indicated for heptatonic scales, but the principle remains the same.
4.4.1. In thirds


4.4.2. In fourths


4.4.3. In fifths


4.4.4. In sixths


4.4.5. In sevenths


4.4.6. In octaves


4.5. Harmonizing Scales
Intervallic patterns can be generalized to breaking down scales into triads and seventh arpeggios. Pentatonic scales can be harmonized in quartal chords, too.
4.5.1. Triads built in thirds


4.5.2. Triads built in fourths


4.5.3. Triads built in fifths


4.5.4. Seventh arpeggios


4.5.5. Arpeggios and their upper structure

4.5.6. Pedals
Pedals are another way to play several sounds at the same time. The pedal note is usually a rather neutral tone (root or fifth). Fingerings and picking can be tricky on the guitar.


4.6. Chord Scales
Chord scales can be played using any inversion of any chord form (Drop 2, etc.) on all possible string groups.
4.6.1. Chord scales for the main modes
| Scale or Mode | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ionian | I\(^\Delta\) | IIm\(^7\) | IIIm\(^7\) | IV\(^\Delta\) | V\(^7\) | VIm\(^7\) | VII\(^\varnothing\) | |||||
| Dorian | Im\(^7\) | IIm\(^7\) | \(\flat\mathrm{III}^\Delta\) | IV\(^7\) | Vm\(^7\) | VI\(^\varnothing\) | \(\flat\mathrm{VII}^\Delta\) | |||||
| Phrygian | Im\(^7\) | \(\flat\mathrm{II}^\Delta\) | \(\flat\mathrm{III}^7\) | IVm\(^7\) | V\(^\varnothing\) | \(\flat\mathrm{VI}^\Delta\) | \(\flat\mathrm{VIIm}^7\) | |||||
| Lydian | I\(^\Delta\) | II\(^7\) | IIIm\(^7\) | \(\sharp\mathrm{IV}^\varnothing\) | V\(^\Delta\) | VIm\(^7\) | VIIm\(^7\) | |||||
| Mixolydian | I\(^7\) | IIm\(^7\) | III\(^\varnothing\) | IV\(^\Delta\) | Vm\(^7\) | VIm\(^7\) | \(\flat\mathrm{VII}^\Delta\) | |||||
| Aeolian | Im\(^7\) | II\(^\varnothing\) | \(\flat\mathrm{III}^\Delta\) | IVm\(^7\) | Vm\(^7\) | \(\flat\mathrm{VI}^\Delta\) | \(\flat\mathrm{VII}^7\) | |||||
| Locrian | I\(^\varnothing\) | \(\flat\mathrm{II}^\Delta\) | \(\flat\mathrm{IIIm}^7\) | IVm\(^7\) | \(\flat\mathrm{V}^\Delta\) | \(\flat\mathrm{VI}^7\) | \(\flat\mathrm{VIIm}^7\) | |||||
| Minor melodic | Im\(^\Delta\) | IIm\(^7\) | \(\flat\mathrm{III}^{\Delta\sharp5}\) | IV\(^7\) | V\(^7\) | VI\(^\varnothing\) | VII\(^\varnothing\) | |||||
| Javanese | Im\(^7\) | \(\flat\mathrm{II}^{\Delta\sharp5}\) | \(\flat\mathrm{III}^7\) | IV\(^7\) | V\(^\varnothing\) | VI\(^\varnothing\) | \(\flat\mathrm{VIIm}^\Delta\) | |||||
| Lydian augmented | I\(^{\Delta\sharp5}\) | II\(^7\) | III\(^7\) | \(\sharp\mathrm{IV}^\varnothing\) | \(\sharp\mathrm{V}^\varnothing\) | VIm\(^\Delta\) | VIIm\(^7\) | |||||
| Lydian dominant | I\(^7\) | II\(^7\) | III\(^\varnothing\) | \(\sharp\mathrm{IV}^\varnothing\) | Vm\(^\Delta\) | VIm\(^7\) | \(\flat\mathrm{VII}^{\Delta\sharp5}\) | |||||
| Aeolian dominant | I\(^7\) | II\(^\varnothing\) | III\(^\varnothing\) | IVm\(^\Delta\) | Vm\(^7\) | \(\flat\mathrm{VI}^{\Delta\sharp5}\) | \(\flat\mathrm{VIIm}^7\) | |||||
| Locrian melodic | I\(^\varnothing\) | II\(^\varnothing\) | \(\flat\mathrm{IIIm}^\Delta\) | IVm\(^7\) | \(\flat\mathrm{V}^{\Delta\sharp5}\) | \(\flat\mathrm{VI}^7\) | \(\flat\mathrm{VII}^7\) | |||||
| Superlocrian | I\(^\varnothing\) | \(\flat\mathrm{IIm}^\Delta\) | \(\flat\mathrm{IIIm}^7\) | \(\flat\mathrm{IV}^{\Delta\sharp5}\) | \(\flat\mathrm{V}^7\) | \(\flat\mathrm{VI}^7\) | \(\flat\mathrm{VII}^\varnothing\) | |||||
| Harm. minor | Im\(^\Delta\) | II\(^\varnothing\) | \(\flat\mathrm{III}^{\Delta\sharp5}\) | IVm\(^7\) | V\(^7\) | \(\flat\mathrm{VI}^\Delta\) | VII\(^{\circ7}\) | |||||
| Locrian harmonic | I\(^\varnothing\) | \(\flat\mathrm{II}^{\Delta\sharp5}\) | \(\flat\mathrm{IIIm}^7\) | IV\(^7\) | \(\flat\mathrm{V}^\Delta\) | VI\(^{\circ7}\) | \(\flat\mathrm{VIIm}^\Delta\) | |||||
| Ionian augmented | I\(^{\Delta\sharp5}\) | IIm\(^7\) | III\(^7\) | IV\(^\Delta\) | \(\sharp\mathrm{V}^{\circ7}\) | VIm\(^{\Delta}\) | VII\(^\varnothing\) | |||||
| Romanian | Im\(^7\) | II\(^7\) | \(\flat\mathrm{III}^\Delta\) | \(\sharp\mathrm{IV}^{\circ7}\) | Vm\(^\Delta\) | VI\(^\varnothing\) | \(\flat\mathrm{VII}^{\Delta\sharp5}\) | |||||
| Phrygian dominant | V\(^7\) | \(\flat\mathrm{II}^\Delta\) | III\(^{\circ7}\) | IVm\(^\Delta\) | V\(^\varnothing\) | \(\flat\mathrm{VI}^{\Delta\sharp5}\) | \(\flat\mathrm{VIIm}^7\) | |||||
| Lydian harmonic | I\(^\Delta\) | \(\sharp\mathrm{II}^{\circ7}\) | IIIm\(^\Delta\) | \(\sharp\mathrm{IV}^\varnothing\) | V\(^{\Delta\sharp5}\) | VIm\(^7\) | VII\(^7\) | |||||
| Harmonic altered | I\(^{\circ7}\) | \(\flat\mathrm{IIm}^\Delta\) | \(\flat\mathrm{III}^\varnothing\) | \(\flat\mathrm{IV}^{\Delta\sharp5}\) | \(\flat\mathrm{Vm}^7\) | \(\flat\mathrm{VI}^7\) | \(\flat\flat\mathrm{VII}^\Delta\) | |||||
| Harmonic major | I\(^\Delta\) | II\(^\varnothing\) | IIIm\(^7\) | IVm\(^\Delta\) | V\(^7\) | \(\flat\mathrm{VI}^{\Delta\sharp5}\) | VII\(^{\circ7}\) | |||||
| Superphrygian | Im\(^7\) | \(\flat\mathrm{IIm}^\Delta\) | \(\flat\mathrm{III}^7\) | \(\flat\mathrm{IV}^{\Delta\sharp5}\) | V\(^{\circ7}\) | \(\flat\mathrm{VI}^\Delta\) | \(\flat\mathrm{VII}^\varnothing\) | |||||
| Lydian minor | Im\(^\Delta\) | II\(^7\) | \(\flat\mathrm{III}^{\Delta\sharp5}\) | \(\sharp\mathrm{IV}^{\circ7}\) | V\(^\Delta\) | VI\(^\varnothing\) | VIIm\(^7\) | |||||
| Unitonic | I\(+\) | II\(+\) | III\(+\) | \(\flat\mathrm{V}+\) | \(\flat\mathrm{VI}+\) | \(\flat\mathrm{VII}+\) | ||||||
| Augmented | I\(+\) | \(\flat\mathrm{III}+\) | \(\flat\mathrm{VI}+\) | V\(+\) | \(\flat\mathrm{VI}+\) | VII\(+\) | ||||||
| Diminished | I\(^{\circ7}\) | II\(^{\circ7}\) | \(\flat\mathrm{III}^{\circ7}\) | IV\(^{\circ7}\) | \(\flat\mathrm{V}^{\circ7}\) | VI\(^{\circ7}\) | \(\flat\flat\mathrm{VII}^{\circ7}\) | VII\(^{\circ7}\) |
4.6.2. The Barry HARRIS Approach (Parallel Motion)
Besides regular chord scales, it is possible to link the successive inversions of a chord with diminished passing chords. It is a particular application of harmonized bebop scales. This trick can be applied to any heptatonic scale with either a major sixth or a minor seventh. The diminished passing chord corresponds to the major seventh (chord tone or passing tone), ninth, eleventh and minor sixths (passing tone) or \(\flat13\). Here are examples in Drop 2, for the most common chords.







In practice, the system taught by Barry HARRIS focuses on four of these scales:
- Major diminished (ionian be-bop);
- Minor diminished (minor melodic be-bop;
- Dominant diminished (aeolian be-bop);
- Dominant \(\flat5\) diminished.
Barry Harris's system makes parallel (see above), oblique and contrary motions much easier.
4.6.3. Oblique Motion (Barry HARRIS)
To go through the different chord tones, keeping the bass constant, we just need to cycle through the different chord voicings (octave chord, Drop 2, Drop 3, Drop 2,4, double octave chord, and back), for all chord qualities. In C6:

It also works for all other inversions. In C6/E:

In C6/G:

In C6/A:

Inversely, we can cycle through the same chord voicing sequence if one wants to keep the soprano voice constant and vary the bass note. In C6:

and so on for all the other inversions.
4.6.4. Contrary Motion (Barry HARRIS)
It is possible to have the bass and soprano voices to move contrarily along the scales. Thomas ECHOLS calls that the "elevator". In C\(^6\), it gives:

4.6.5. Quartal harmony
Scales can also be harmonized in quartal triads and sevenths chords. My personal taste however makes me lean more toward the harmonization of "no-avoid-note scales", in a more modal context.


Quartal chords can also be inverted the same way as regular chords.
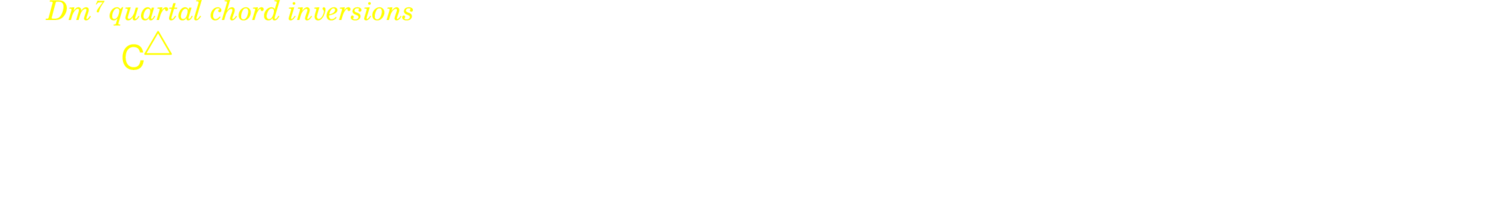
Quartal harmony works particularly well with pentatonic scales.

4.7. Rhythmic Patterns
The following rhythmic patterns can be applied either to ternary or binary beats provided that the total number of counts is conserved. For instance, the four-on-six patterns can be played these two different ways:

There are many more patterns, but four notes is a good base, as it is the way we conceive improvisation in Jazz (four notes of a seventh arpeggio, four-note scale fragment, Coltrane patterns on Giant Steps, etc.).
4.7.1. Four on six patterns





4.7.2. Four on eight patterns






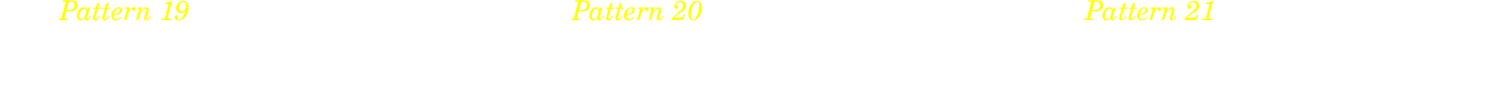
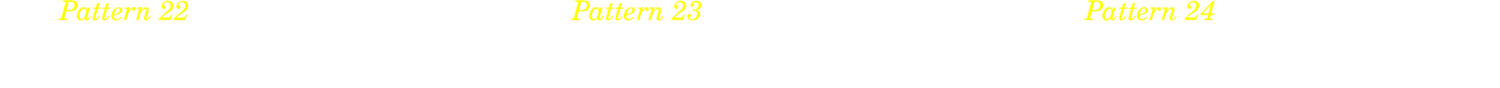








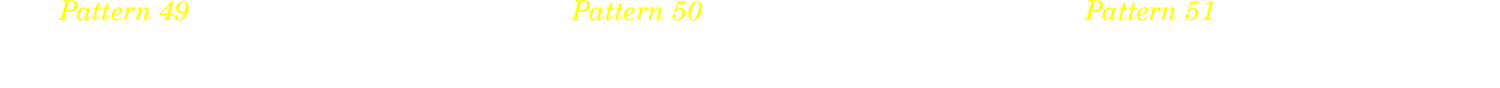



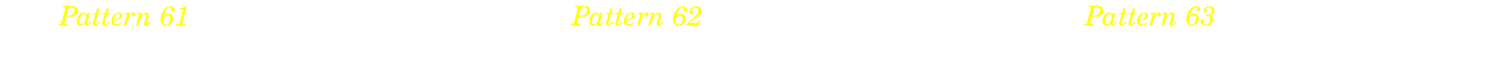
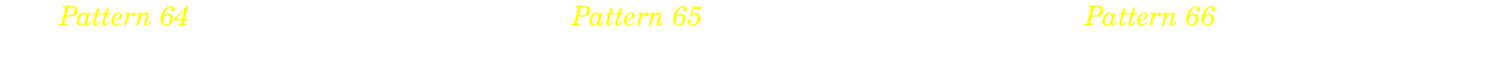


5. IMPROVISING THROUGH CHORD CHANGES
5.1. Chord/Scale Relation
We list the most obvious melodic elements to play on different types of chords. More combinations are possible, but these are a good start. The substituted arpeggios can be incorporated into solo lines or as block chords.
5.1.1. Most common chords
| Melodic element | |||||||
|---|---|---|---|---|---|---|---|
| C lydian mode | 1 | 3 | 5 | 7 | 9 | \(\sharp11\) | 13 |
| C major pentatonic | 1 | 3 | 5 | 9 | 13 | ||
| G major pentatonic | 3 | 5 | 7 | 9 | 13 | ||
| D major pentatonic | 3 | 7 | 9 | \(\sharp11\) | 13 | ||
| Am\(^7\) arpeggio | 1 | 3 | 5 | 13 | |||
| C\(^\Delta\) arpeggio | 1 | 3 | 5 | 7 | |||
| Em\(^7\) arpeggio | 3 | 5 | 7 | 9 | |||
| G\(^\Delta\) arpeggio | 5 | 7 | 9 | \(\sharp11\) | |||
| Bm\(^7\) arpeggio | 7 | 9 | \(\sharp11\) | 13 | |||
| D\(^7\) arpeggio | 1 | 9 | \(\sharp11\) | 13 | |||
| F\(\sharp^\varnothing\) | 1 | 3 | \(\sharp11\) | 13 |
| Melodic element | |||||||
|---|---|---|---|---|---|---|---|
| C minor melodic | 1 | 3m | 5 | 7 | 9 | 11 | 13 |
| F dominant pentatonic | 1 | 3m | 5 | 11 | 13 | ||
| E\(\flat\) unitonic pentatonic | 3m | 5 | 7 | 11 | 13 | ||
| G dominant pentatonic | 7 | 9 | 11 | 13 | |||
| A\(^\varnothing\) arpeggio | 1 | 3m | 5 | 13 | |||
| Cm\(^\Delta\) arpeggio | 1 | 3m | 5 | 7 | |||
| E\(\flat^{\Delta\sharp5}\) arpeggio | 3m | 5 | 7 | 9 | |||
| G\(^7\) arpeggio | 5 | 7 | 9 | 11 | |||
| B\(^\varnothing\) arpeggio | 7 | 9 | 11 | 13 | |||
| Dm\(^7\) arpeggio | 1 | 9 | 11 | 13 | |||
| F\(^7\) | 1 | 3m | 11 | 13 |
| Melodic element | |||||||
|---|---|---|---|---|---|---|---|
| G lydian dominant mode | 1 | 3 | 5 | \(\flat7\) | 9 | \(\sharp11\) | 13 |
| G dominant pentatonic | 1 | 3 | 5 | \(\flat7\) | 9 | ||
| D kumoi pentatonic | 3 | 5 | \(\flat7\) | 9 | 13 | ||
| A harmonic major pentatonic | 3 | \(\flat7\) | 9 | \(\sharp11\) | 13 | ||
| G\(^7\) arpeggio | 1 | 3 | 5 | \(\flat7\) | |||
| B\(^\varnothing\) arpeggio | 3 | 5 | \(\flat7\) | 9 | |||
| Dm\(^\Delta\) arpeggio | 5 | \(\flat7\) | 9 | \(\sharp11\) | |||
| F\(^{\Delta\sharp5}\) arpeggio | \(\flat7\) | 9 | \(\sharp11\) | 13 | |||
| A\(^7\) arpeggio | 1 | 9 | \(\sharp11\) | 13 | |||
| C\(\sharp^\varnothing\) arpeggio | 1 | 3 | \(\sharp11\) | 13 | |||
| E\(^7\) | 1 | 3 | 5 | 13 |
| Melodic element | |||||||
|---|---|---|---|---|---|---|---|
| D dorian mode | 1 | 3m | 5 | \(\flat7\) | 9 | 11 | 13 |
| F major pentatonic | 1 | 3m | 5 | \(\flat7\) | 9 | ||
| C major pentatonic | 3m | 5 | \(\flat7\) | 9 | 13 | ||
| G major pentatonic | 3m | \(\flat7\) | 9 | 11 | 13 | ||
| Dm\(^7\) arpeggio | 1 | 3m | 5 | \(\flat7\) | |||
| F\(^\Delta\) arpeggio | 3m | 5 | \(\flat7\) | 9 | |||
| Am\(^7\) arpeggio | 5 | \(\flat7\) | 9 | 11 | |||
| C\(^{\Delta}\) arpeggio | \(\flat7\) | 9 | 11 | 13 | |||
| Em\(^7\) arpeggio | 1 | 9 | 11 | 13 | |||
| G\(^7\) arpeggio | 1 | 3m | 11 | 13 | |||
| B\(^\varnothing\) | 1 | 3m | 5 | 13 |
| Melodic element | |||||||
|---|---|---|---|---|---|---|---|
| D locrian melodic mode | 1 | 3m | \(\flat5\) | \(\flat7\) | 9 | 11 | \(\flat13\) |
| F kumoi pentatonic | 1 | 3m | \(\flat5\) | \(\flat7\) | 11 | ||
| C harmonic major pentatonic | 1 | \(\flat5\) | \(\flat7\) | 9 | 11 | ||
| G javanese pentatonic | 1 | \(\flat5\) | 9 | 11 | \(\flat13\) | ||
| D\(^\varnothing\) arpeggio | 1 | 3m | \(\flat5\) | \(\flat7\) | |||
| Fm\(^\Delta\) arpeggio | 3m | \(\flat5\) | \(\flat7\) | 9 | |||
| A\(\flat^{\Delta\sharp5}\) arpeggio | \(\flat5\) | \(\flat7\) | 9 | 11 | |||
| C\(7^{}\) arpeggio | \(\flat7\) | 9 | 11 | \(\flat13\) | |||
| E\(^\varnothing\) arpeggio | 1 | 9 | 11 | \(\flat13\) | |||
| Gm\(^7\) arpeggio | 1 | 3m | 11 | \(\flat13\) | |||
| B\(\flat^7\) | 1 | 3m | 5 | \(\flat13\) |
| Melodic element | ||||||||
|---|---|---|---|---|---|---|---|---|
| G diminished mode | 1 | 3m | \(\flat5\) | \(\flat\flat7\) | 9 | 11 | \(\flat13\) | 7 |
| B diminished pentatonic | 1 | 3m | \(\flat5\) | \(\flat\flat7\) | 9 | |||
| B\(^{\circ7}\) arpeggio | 1 | 3m | \(\flat5\) | \(\flat\flat7\) | ||||
| C\(^{\circ7}\) arpeggio | 9 | 11 | \(\flat13\) | 7 |
5.1.2. Altered dominant chords
| Melodic element | |||||||
|---|---|---|---|---|---|---|---|
| G superlocrian mode | \(\flat5\) | \(\flat7\) | \(\flat9\) | 3 | \(\flat13\) | 1 | \(\sharp9\) |
| D\(\flat\) dominant pentatonic | \(\flat5\) | \(\flat7\) | \(\flat9\) | 3 | \(\flat13\) | ||
| A\(\flat\) kumoi pentatonic | \(\flat7\) | \(\flat9\) | 3 | \(\flat13\) | \(\sharp9\) | ||
| E\(\flat\) harmonic major pentatonic | \(\flat7\) | 3 | \(\flat13\) | 1 | \(\sharp9\) | ||
| D\(\flat^7\) arpeggio | \(\flat5\) | \(\flat7\) | \(\flat9\) | 3 | |||
| F\(^\varnothing\) arpeggio | \(\flat7\) | \(\flat9\) | 3 | \(\flat13\) | |||
| A\(\flat\mathrm{m}^\Delta\) arpeggio | \(\flat9\) | 3 | \(\flat13\) | 1 | |||
| B\(^{\Delta\sharp5}\) arpeggio | 3 | \(\flat13\) | 1 | \(\sharp9\) | |||
| E\(\flat^7\) arpeggio | \(\flat5\) | \(\flat13\) | 1 | \(\sharp9\) | |||
| G\(^\varnothing\) arpeggio | \(\flat5\) | \(\flat7\) | 1 | \(\sharp9\) | |||
| B\(\flat^7\) | \(\flat5\) | \(\flat7\) | \(\flat9\) | \(\sharp9\) |
| Melodic element | ||||||
|---|---|---|---|---|---|---|
| G unitonic mode | 1 | 3 | \(\sharp5\) | \(\flat7\) | 9 | \(\sharp11\) |
| G unitonic pentatonic | 1 | 3 | \(\sharp5\) | \(\flat7\) | 9 | |
| G+ arpeggio | 1 | 3 | \(\sharp5\) | |||
| A+ arpeggio | \(\flat7\) | 9 | \(\sharp11\) |
| Melodic element | ||||||||
|---|---|---|---|---|---|---|---|---|
| A\(\flat\) diminished mode | 1 | 3 | \(\flat5\) | \(\flat7\) | \(\flat9\) | \(\sharp11\) | 13 | \(\sharp9\) |
| F diminished pentatonic | 1 | 3 | \(\flat5\) | \(\flat7\) | \(\flat9\) | |||
| A\(\flat\) diminished arpeggio | 3 | \(\flat5\) | \(\flat7\) | \(\flat9\) | ||||
| G diminished arpeggio | 1 | \(\sharp11\) | 13 | \(\sharp9\) |
5.1.3. Derived chords
Several commonly used chords are the inversion of other ones.
| Major tonality chord | Chord equivalent | Minor tonality chord | Chord equivalent | |||
|---|---|---|---|---|---|---|
| C\(^6\) | ⇔ | Am\(^7/\mathrm{C}\) | Cm\(^6\) | ⇔ | A\(^\varnothing/\mathrm{C}\) | |
| (C lydian) | (A dorian) | (C minor melodic) | (A locrian melodic) | |||
| G\(^{9sus}\) | ⇔ | Dm\(^7/\mathrm{G}\) | G\(^{7\flat9sus}\) | ⇔ | D\(^\varnothing/\mathrm{G}\) | |
| (G mixolydian) | (D dorian) | (G javanese) | (D locrian melodic) | |||
| G\(^{7\flat9}\) | ⇔ | D\(^{\circ7}/\mathrm{G}\) | G\(^{7\flat9\flat5}\) | ⇔ | D\(\flat^{7}/\mathrm{G}\) | |
| (G diminished dominant) | (D diminished dominant) | (G superlocrian) | (D\(\flat\) lydian dominant) |
5.2. Forward Motion
5.2.1. Resolution
To make good sounding phrases, it is important to resolve chord tones on the strong beats. This resolution is heard better if it is:
- down from a scale tone;
- up from a chromatic tone;
- down a fifth;
- up a fourth.
For instance, resolving A\(^{7alt}\) to Dm\(^6\) can look like that:


The way to implement these resolutions using arpeggios, scales and their respective patterns, with octave displacement are virtually infinite. For instance:

5.2.2. Bebop scales
Bebop scales are an easy way to make sure that, when played ascending or descending, we have a chord tone on each strong beat. For heptatonic scales, bebop scales are built by adding a chromatic passing tone:
- On the minor sixth, for major and minor sixth cords;
- On the major seventh, for chords having a minor sevenths.
We note that we can not build a scale for chords with a major sevenths, as there is not room between this tone and the root. We also note that the diminished scale is already synchronized. Played in eight notes, we have the following bebop scales, among many others.


Bebop scales can also be played in triplet. On the guitar, they sound good played three notes per string, with the middle note (the second on each string) on the beat. This way, it gives a natural accent on the up beat, and can accommodate slurring as well as economy picking.

That way, we still get a chord tone on beats one and three.
5.2.3. The most useful Jazz trick
From a practical point of view, it is not always easy to improvise nice phrases across chord changes, as we have to visualize/hear two different chords at once, and target different chord tones. A highly effective shortcut to that problem consists in learning what are the tones of the next chord in the reference frame of the current chord. It gets even simpler if we also realize that the majority of chord changes in Jazz standards are going to a chord a fourth higher (or a fifth lower), such as in a VI II V I IV changes:
| Current chord | Next chord | |
|---|---|---|
| VI\(^{7alt}\) | ↔ | IIm\(^7\) |
| IIm\(^7\) | ↔ | V\(^7\) |
| V\(^7\) | ↔ | I\(^\Delta\) |
| I\(^\Delta\) | ↔ | IV\(^\Delta\) |
| II\(^\varnothing\) | ↔ | V\(^{7alt}\) |
| V\(^{7alt}\) | ↔ | Im\(^6\) |
| 4 | ↔ | 1 |
| 6m | ↔ | 3m |
| 6 | ↔ | 3 |
| 7 | ↔ | \(\flat5\) |
| 1 | ↔ | 5 |
| 2m | ↔ | \(\sharp5\) |
| 2 | ↔ | 6 |
| 3m | ↔ | \(\flat7\) |
| 3 | ↔ | 7 |
| \(\flat5\) | ↔ | \(\flat9\) |
| 5 | ↔ | 9 |
In other words, when playing across a IIm\(^7\) V\(^7\) change, thinking about resolving the IIm7 on its sixth can lead to smoother phrases than thinking about the third of the V\(^7\), although both are the same note (B in C major).
Tritone substitutions are also useful to know:
| Current chord | Next chord | |
|---|---|---|
| \(\flat\mathrm{II}^{7}\) | ↔ | I\(^\Delta\) |
| \(\flat\mathrm{II}^{7}\) | ↔ | Im\(^6\) |
| \(\flat\mathrm{II}^{7}\) | ↔ | I\(^7\) |
| 7 | ↔ | 1 |
| 2 | ↔ | 3m |
| 3m | ↔ | 3 |
| \(\flat5\) | ↔ | 5 |
| 6m | ↔ | 6 |
| 6 | ↔ | \(\flat7\) |
| \(\flat7\) | ↔ | 7 |
| 2m | ↔ | 9 |
Backdoor resolution:
| Current chord | Next chord | |
|---|---|---|
| \(\flat\mathrm{VII}^{7}\) | ↔ | I\(^\Delta\) |
| \(\flat\mathrm{VII}^{7}\) | ↔ | Im\(^6\) |
| \(\flat\mathrm{VII}^{7}\) | ↔ | I\(^7\) |
| 2 | ↔ | 1 |
| 4 | ↔ | 3m |
| \(\flat5\) | ↔ | 3 |
| 6 | ↔ | 5 |
| 7 | ↔ | 6 |
| 1 | ↔ | \(\flat7\) |
| 2m | ↔ | 7 |
| 3 | ↔ | 9 |
The difficult transition in Coltrane changes (Countdown, Giant Steps):
| Current chord | Next chord | |
|---|---|---|
| I\(^\Delta\) | ↔ | III\(^7\) |
| 3m | ↔ | 1 |
| 5 | ↔ | 3 |
| \(\flat7\) | ↔ | 5 |
| 2m | ↔ | \(\flat7\) |
| 4 | ↔ | 9 |
5.2.4. II V I with pentatonics
| Dm\(^7\) | G\(^{7alt}\) | C\(^\Delta\) |
|---|---|---|
| D minor pentatonic | E\(\flat\) minor pentatonic | E minor pentatonic |
| A minor pentatonic | B\(\flat\) minor pentatonic | B minor pentatonic |
5.3. Common Chord Changes
Comping and improvising through chord changes can be greatly simplified if we work out specific chord patterns that are all over the place in standards. These changes can be practiced in all keys, all tempos and all chord durations (2/4, 3/4, 4/4, etc.).
5.3.1. Two-chord changes
Once we can improvise on one chord, the next step before going to a full 32-bar standard is to develop a vocabulary over two-chord changes. The most useful ones are the following.
| Name | First chord | Second chord |
|---|---|---|
| Major perfect cadence | V\(^{7}\) | I\(^\Delta\) |
| Minor perfect cadence | V\(^{7}\) | I\(^6\) |
| Dominant perfect cadence | V\(^7\) | I\(^7\) |
| Major plagal cadence | I\(^\Delta\) | IV\(^\Delta\) |
| Minor plagal cadence | I\(^6\) | IV\(^6\) |
| Dominant plagal cadence | I\(^7\) | IV\(^7\) |
| Major II V | IIm\(^7\) | V\(^7\) |
| Minor II V | II\(^\varnothing\) | V\(^7\) |
5.3.2. II V Is
II V I are the building blocks of Jazz standards. There are a few common substitutions (in the key of C):
| Name | II | V | I |
|---|---|---|---|
| Major | Dm\(^7\) | G\(^7\) | C\(^\Delta\) |
| Tritone sub. | A\(\flat\mathrm{m}^7\) | D\(\flat^7\) | C\(^\Delta\) |
| Backdoor | Fm\(^7\) | B\(\flat^7\) | C\(^\Delta\) |
| Minor | D\(^\varnothing\) | G\(^7\) | C\(^6\) |
| Minor w/ tritone sub. | D\(^\varnothing\) | D\(\flat^7\) | C\(^6\) |
5.3.3. Major and minor tonal cycles
The following are found in many A A B A standards.

5.3.4. Major blues
5.3.5. Minor blues

5.3.6. Swedish blues
A good II V workout:
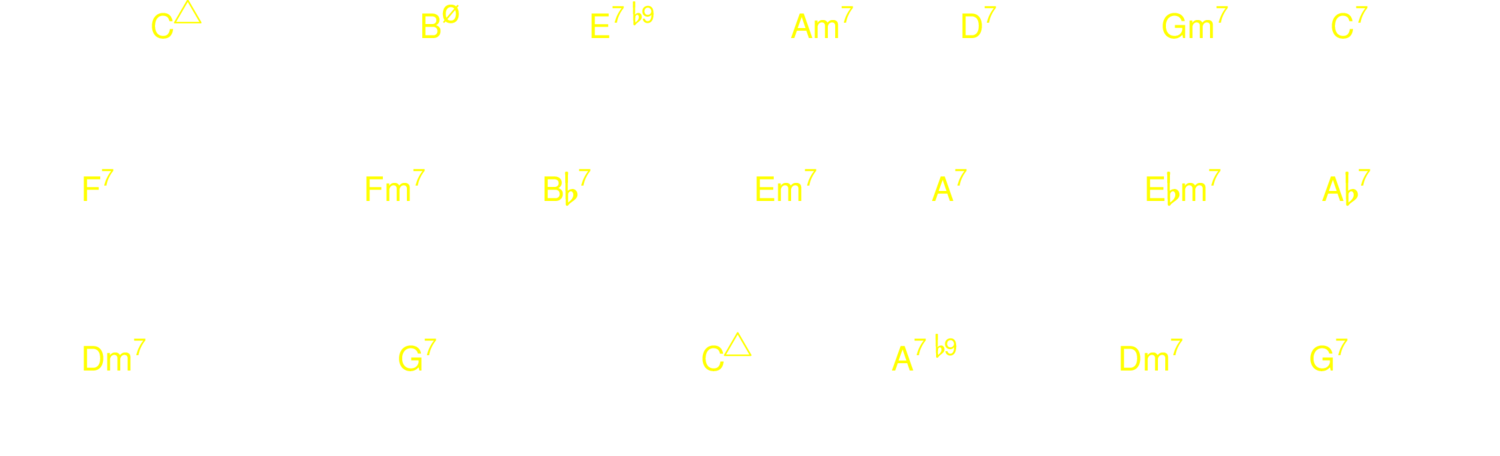
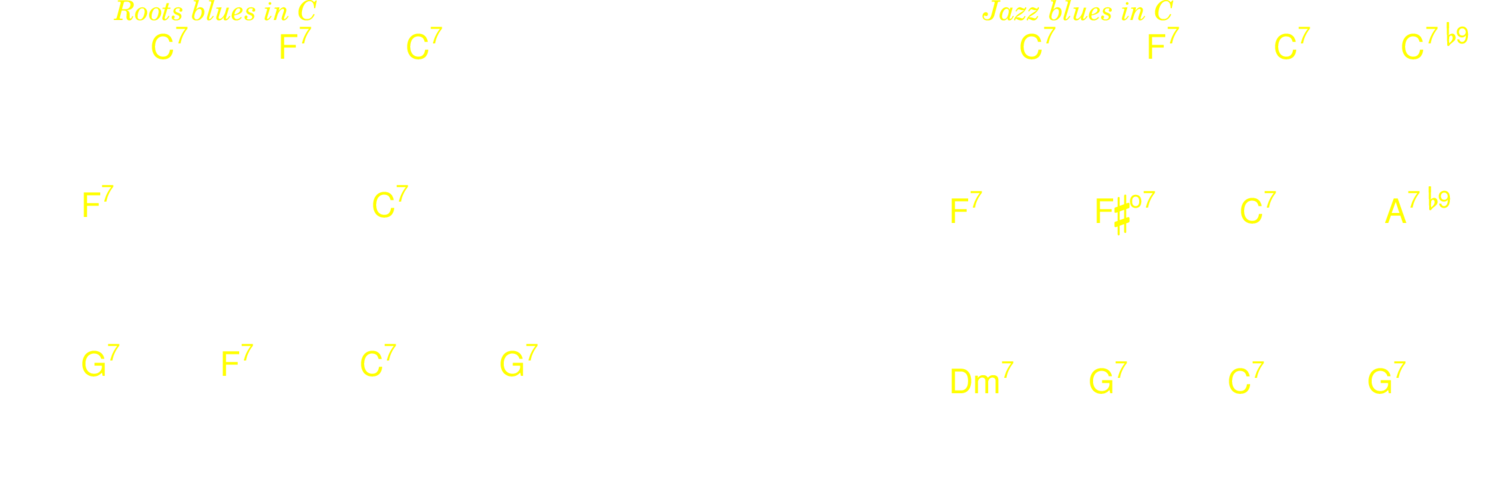
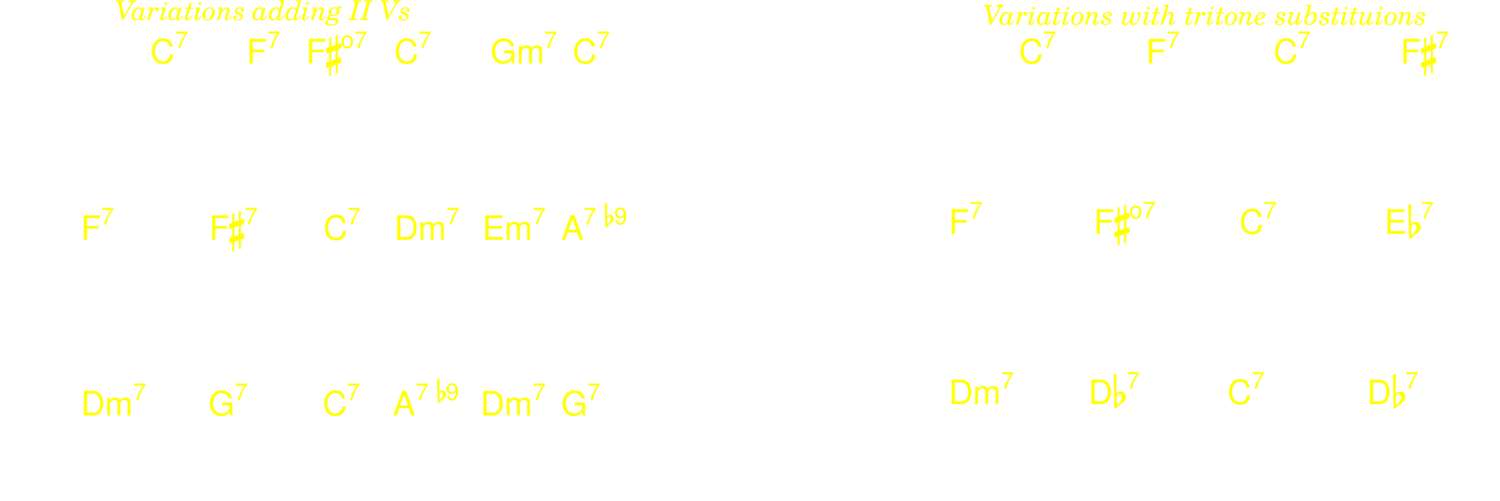
5.3.7. Rhythm changes
The structure of rhythm changes is A A B A. Here are a few common variations on the A.
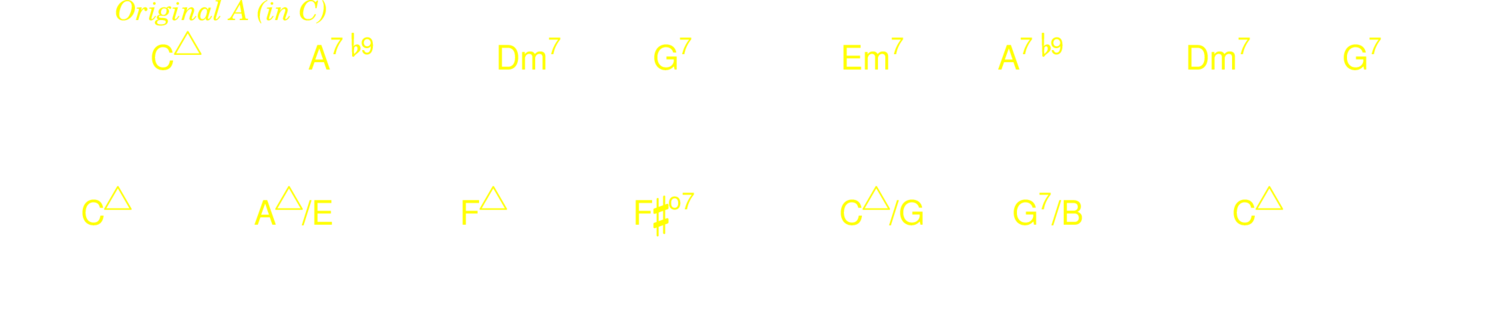
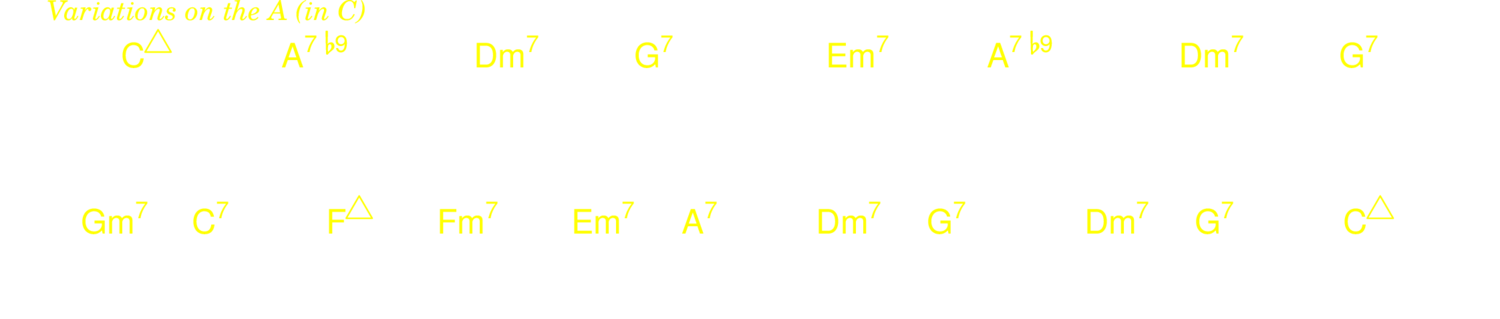
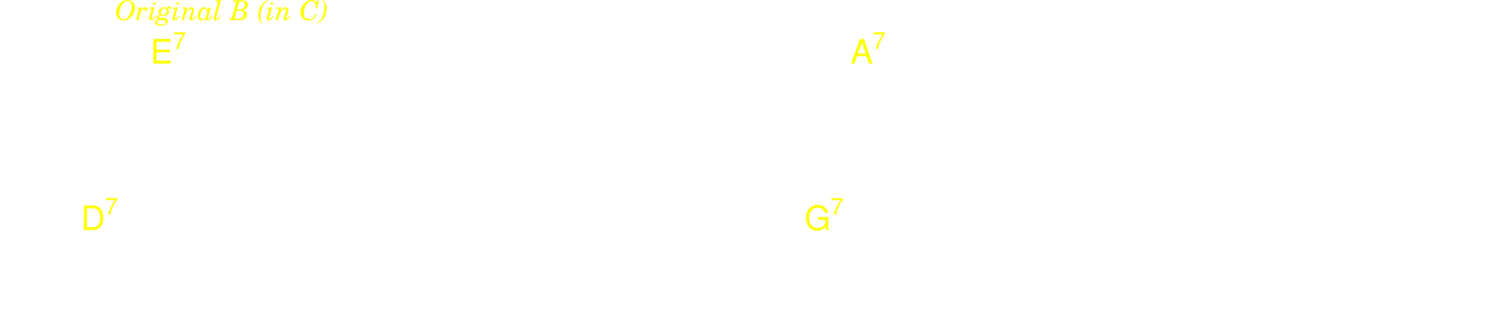
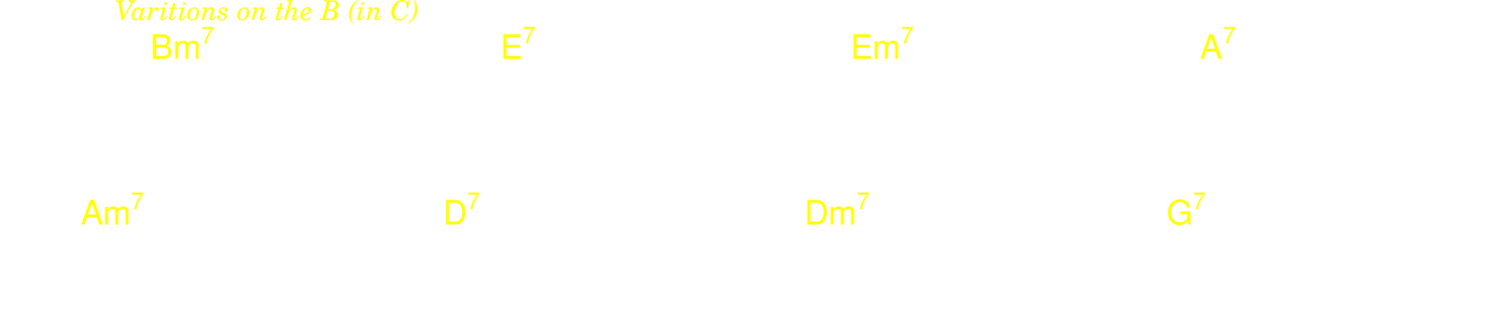
5.3.8. Coltrane changes
This is the A of Countdown.

5.4. Reharmonization Techniques
Reharmonization is a big deal in Jazz. The following possibilities can be applied to comping and soloing. Some are very smooth sounding, some can be spicy.
5.4.1. Dominant chords



Diminished dominant substitution:

Superlocrian dominant substitution:

Tritone substitutions:



Lydian dominant substitution:

Unitonic dominant substitution:

Bluesy static dominant chord:

5.4.2. Minor chords


Chromatic Elaboration of Static Harmony (CESH) or line-cliché:


Deceptive cadence:

Tonic minor resolution:

Secondary dominant substitution:


5.4.3. Major chords








5.5. Practicing Standards
Here is a non-exhaustive list of some things to practice when working on a tune. Not all are possible. We can not practice the same way a ballad and an up-tempo bebop tune, but all these ideas are worth considering.
5.5.1. Listening
- Listen to different versions of the tune. Check the differences in tonality, phrasing, harmony, etc.
- Come up with a preferred version (write it up). If this tune will be mainly played in a band, it can be reharmonized and modified. Otherwise, if it is a standard to be played with random people, it should not be far from the Real Book version.
- Listen to the contrast in dynamics and texture between the theme and the solos, and between the A and the B, and try to reproduce it in the following.
- Prepare a backing track. Try also to play with the record.
5.5.2. Exposing the melody
- Single notes.
- Practice the melody in different areas of the neck and different registers.
- Adapt the fingering to optimize the phrasing (slurs, slides, etc.).
- Try adding embellishments to the harmony:
- Appoggiatura and other effects;
- Tags and pick-ups;
- Rhythmic variations.
- If the melody has some space, try out questions and answers:
- Answer the melody with other melodic phrases;
- Answer it with chord voicings.
- Harmonized melody.
- It is not always possible to systematically achieve these over the whole tune. However, it might be possible on some particular fragments.
- Try all possible dyad harmonization:
- Octave;
- Thirds;
- Tenths;
- Sixths;
- Fourths;
- Fifths;
- Sevenths;
- Seconds.
- Also try harmonizing the melody with non-constant intervals:
- Contrary motions;
- Pedals.
- Harmonize the melody in chords without a bass (arbitrary inversions). This harmonized melody is meant to be played with a bass player.
- In triads (including quartal triads) to highlight the upper structure of the chord.
- In seventh chords.
- Try all possible dyad harmonization:
- Solo chord melody.
- The following are meant to be played without accompaniment, either as a standalone version of the tune, or as an intro to a band version.
- Work out a melody with chords and their bass. It does not have to be dense and can be played rubato, with embellishments between chords.
- Work out a melody with a bass line. If possible the bass line can be a walking bass.
- Work out a full chord melody, like a composed classical piece.
5.5.3. Comping
- Look for rhythmic patterns matching the vibe of the tune. In doubt, try all possible combinations.
- Practice all chord forms and inversions on the tune.
- Explore the sound of different enrichments (9, 11, 13).
- Try out different reharmonizations.
- Practice approaching the next chords with:
- Chromatic movements;
- Diatonic/diminished movements;
- Same but with a special treatment for the higher voice (constant or contrary motion; examples in Pierre CULLAZ's book).
- Play the tune with shell chords, in quarter notes. On fast tempos, change chords every bar. On slower tempos, try moving the chords smoothly to the next. Use diatonic or diminished passing chords.
- Practice improvising walking bass lines.
- Practice improvising walking bass lines with chord fragments (Tuck ANDRESS's way).
- Look for original approaches:
- Slaps;
- Pick vs fingerstyle;
- Compose riffs and find chord licks;
- Use open strings;
- Try out different sounds (equalization, combination of pick-ups, pedals, etc.).
5.5.4. Soloing
- Listen to other people's solos. Transcribe them if they are particularly great.
- If the tune is particularly hard, compose a few solos to break it.
- Practice forward motion with scales, arpeggios and pentatonics. Exhaust all the possible resolutions from one chord to another. Also find out the common chord tones. This is where most of the work is…
- Look for original approaches:
- Open strings;
- Pinched harmonics;
- Use of effect pedals;
- Exotic scales.