Les théories actuelles modélisant la fission s’attachent à reproduire la fission asymétrique des actinides (Z > 89) mais elles ne prévoient pas la fission d’éléments plus légers comme celle des isotopes de mercure. En particulier, le Mercure-180 (180Hg) présente un comportement inattendu, mis en évidence par des mesures récentes, car il privilégie une cassure en deux noyaux de masses différentes alors que les mercures plus lourds se scindent à peu près symétriquement.
Une équipe de la collaboration DAM-DSM en physique nucléaire (Cophynu) a élaboré un nouveau modèle théorique, SPY (Scission Point Yields), capable de prédire le caractère symétrique ou non de la fission de n’importe quel noyau. Ce modèle repose sur l’étude microscopique du « point de scission », c’est-à-dire du moment exact de la fission où les deux fragments du noyau viennent de se former. Le modèle se base sur les caractéristiques de plus de 7 000 noyaux, évaluées grâce aux outils de calcul intensif du CEA. Il permet de calculer les distributions en masse et en énergie des fragments de fission de tous les noyaux, sans exception, en se basant sur la seule structure des noyaux fils.
La fission en question
La fission nucléaire, bien que connue et étudiée depuis plus de 75 ans, est aujourd’hui encore un phénomène très étudié en physique nucléaire.
La compréhension de ce processus met en jeu un grand nombre de propriétés complexes de la matière nucléaire1 , ce qui fait de la fission un processus très riche pour l’étude de la physique nucléaire dans des conditions extrêmes. L’un des observables physiques les plus étudiées, aussi bien du point de vue expérimental que théorique, est la distribution en masse des noyaux issus de la fission, les fragments de fission.
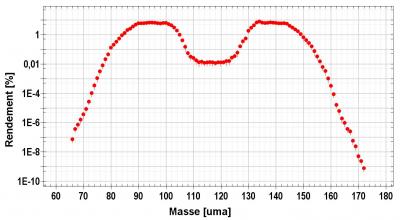
Par exemple, il est bien connu que la fission des éléments plus lourds que l’Actinium, lorsqu’elle se produit à basse énergie, donne lieu à deux noyaux de masses différentes, un noyau lourd et un noyau léger : c'est la fission asymétrique. C’est le cas de l’Uranium (figure 1), l’élément dont la fission est à la base du fonctionnement des réacteurs nucléaires actuels. D’autre part, les noyaux plus légers comme le Plomb (Pb), le Bismuth (Bi) et certains isotopes du Mercure (Hg), fissionnent en deux fragments de masses à peu près égales : c’est la fission symétrique (figure 2).
Ce comportement a été traditionnellement attribué à la structure en couches des fragments qui favorise la formation de noyaux appelés « magiques ».
Fig.1 : Distribution des rendements en masse des fragments issus de la fission thermique du 235U. On voit que les fragments produits lors de la fission du 235U se distribuent de manière asymétrique, avec un fragment lourd (avec une masse autour de 140) et un léger de masse 95 environ.
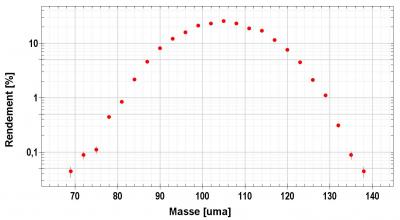
Fig.2 :Dans le cas du 209Bi, la fission est dite symétrique car elle donne lieu principalement à deux fragments de masse 105.
Ces noyaux particuliers possèdent un nombre de protons et neutrons correspondant au remplissage complet des niveaux d’énergie disponibles, les « couches ». Le caractère symétrique ou asymétrique de la distribution de masse des fragments de fission semblait donc plus lié aux caractéristiques des fragments qu’à la dynamique du processus de fission.
Or, une mesure récente [1] a montré que l’isotope de masse 180 du Mercure, bien qu’il se trouve dans la même région de masse que le Pb et le Bi, présente une fission asymétrique (figure 1) alors que ses isotopes plus lourds fissionnent symétriquement. Ce résultat étonnant ne s'explique pas par la seule structure en couche des fragments. Pour expliquer ce phénomène, les théoriciens ont montré qu'il fallait prendre en compte toute la dynamique du noyau qui fissionne.
La structure en couches des fragments de fission n'est pas suffisante pour expliquer le caractère asymétrique ou symétrique de leur distribution en masse.
Le modèle SPY
Dans le cadre de la collaboration en physique nucléaire entre la DAM et la DSM (Cophynu), une équipe de physiciens a réussi à expliquer, dans un même cadre théorique, la fission des actinides et la fission des différents isotopes du Mercure depuis le 180Hg jusqu’au 198Hg.
Le modèle théorique qu’ils ont développé pour « espionner » la fission, baptisé SPY (Scission Point Yields), se base sur un calcul précis de l’énergie disponible pour le système lors de la dernière étape du processus de fission : la scission en deux noyaux. Cette configuration, appelée point de scission, correspond au moment où les deux fragments sont à peine séparés et voient leurs caractéristiques (masse et charge nucléaire) figées. Puisque la quantité d’énergie disponible est reliée à la stabilité du système, le calcul de cette grandeur permet de distinguer les configurations les plus probables (celles avec la plus grande énergie disponible) de celles qui sont les moins favorisées.
Ce modèle a été testé avec les caractéristiques de plus de 7 000 noyaux, évaluées grâce aux outils de calcul intensif du CEA. (base de données Amédée 2)
La structure de chacun de ces noyaux est calculée dans le cadre d’un modèle microscopique utilisant une interaction nucléon-nucléon effective, basée sur la force de Gogny. Le modèle se sert donc des seules informations concernant la structure microscopique des fragments de fission et n’inclut aucune information liée aux caractéristiques du noyau père.
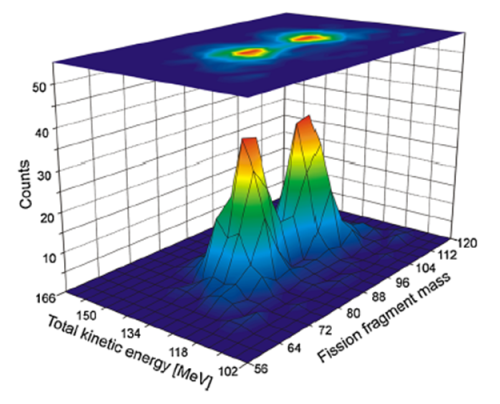
Les résultats du modèle SPY [2] montrent que, dans le cas du 180Hg, tout comme pour la fission induite par neutron du 235U, les configurations asymétriques présentent une énergie disponible plus importante que les configurations symétriques et sont donc plus probables (figure 3). Ceci n’est pas le cas pour le calcul de la fission du 198Hg, où la fragmentation symétrique est favorisée, conformément à ce qui a été observé expérimentalement3 (figure 4).
Fig.3 : Distribution expérimentale des rendements en masse des fragments issus de la fission du 180Hg en fonction de leur énergie cinétique.
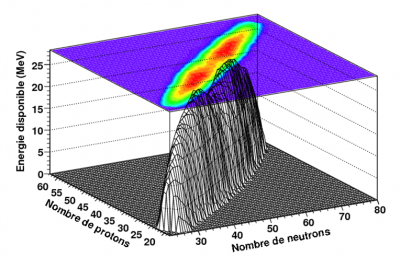
Fig.4 Energie disponible à la scission, en fonction du nombre de neutrons et de protons des fragments, calculée dans le cadre du modèle SPY pour la fission du 180Hg.
Conclusion
En conclusion, le modèle de point de scission SPY établit clairement que la forme générale de la distribution de masse des fragments de fission peut être correctement reproduite en ne tenant compte que de la structure des noyaux fils. La fission du 180Hg n’est donc en rien un cas particulier qui échapperait à l’interprétation générale.
Ce premier succès du modèle valide à la fois le cadre théorique et ses ingrédients, dont la base de données nucléaires Amédée qui, jusqu’à présent, n’avait jamais été utilisée comme outil pour décrire des réactions nucléaires. L’équipe travaille à inclure d’autres caractéristiques des noyaux comme les densités d’états en fonction de l’énergie d’excitation et de la déformation du noyau pour compléter le bilan d’énergie par un traitement statistique qui permettra d’accéder directement aux observables physiques des fragments de fission (probabilité de production, énergie cinétique, énergie d’excitation…).
Ce modèle proposera alors une description microscopique complète de cette étape cruciale du processus de fission qu’est la scission.
[1] A. N. Andreyev et al., Physical Review Letters 105, 252502 (2010)
[2] S. Panebianco et al., Physical Review C 86, 064601 (2012)
Contact : S.Panebianco et S. Hilaire (DAM)
--------------------------------------------------------------------------------
1- Dynamique des systèmes à N-corps, effets collectifs, déformations des noyaux, effets de structure..
2- http://www-phynu.cea.fr/HFB-Gogny.htm
3-Afin de comparer les rendements expérimentaux avec la distribution des énergies disponibles, il faut remarquer que, dans une interprétation statistique du système formé par les deux fragments à la scission, le rendement est, au premier ordre, une fonction exponentielle de l’énergie disponible. Ceci explique pourquoi le creux de la distribution des rendements expérimentaux est plus prononcé que celui de la distribution des énergies disponibles.
• Structure de la matière nucléaire › Dynamique des réactions nucléaires
• Le Département de Physique Nucléaire (DPhN)
• Laboratoire d'études et d'applications des réactions nucléaires (LEARN)
