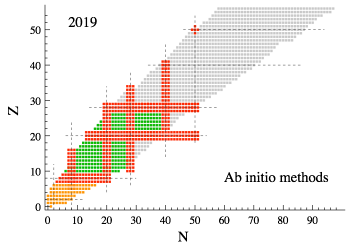
Figure 1: Noyaux accessibles par les méthodes ab initio : méthodes quasi-exactes (orange), méthodes impliquant un espace de valence (vert) et méthodes utilisant un développement sur une fonction d’onde (rouge).
Prédire les propriétés nucléaires à partir d’une description réaliste de l'interaction forte est au cœur des méthodes dites ab initio utilisées en théorie nucléaire de basse énergie. Les calculs ab initio ont longtemps été limités aux noyaux légers ou aux noyaux avec des nombres spécifiques de protons et de neutrons. Les théoriciens de l'Irfu/DPhN ont développé de nouvelles méthodes ab initio qui ont conduit à une augmentation significative du nombre de noyaux prédits par ces approches. La plus récente, appelée théorie des perturbations pour le problème à N corps de Bogoliubov (BMBPT), offre une alternative capable de fournir des résultats de la même précision que les méthodes concurrentes, mais avec un coût de calcul réduit de deux ordres de grandeur. Cela a été rendu possible en autorisant les brisures spontanées des symétries de l’Hamiltonien nucléaire. Ce développement prometteur, ouvrant la voie à des calculs précis de noyaux plus lourds utilisant des ressources informatiques raisonnables, a récemment été publié dans Physics Letter B[1].
Les noyaux atomiques sont des systèmes composés de nucléons, c'est-à-dire de protons et de neutrons, qui interagissent par l'intermédiaire de forces inter-nucléons dont la dynamique est décrite par la théorie des champs de la chromodynamique quantique (QCD). Malheureusement, la QCD présente un caractère non perturbatif aux basses énergies caractérisant le domaine de la structure nucléaire. Dans ce contexte, décrire les propriétés du noyau atomique, de manière systématique et maîtrisée, constitue une tâche extrêmement complexe. Ce problème de longue date (et toujours non résolu) est au cœur de l'approche dite ab initio du problème à N corps en physique nucléaire. Cela nécessite :
i) une modélisation des interactions inter-nucléons qui interviennent dans l'équation de Schrödinger à A corps (une équation aux valeurs propres pour l’Hamiltonien où A est le nombre de nucléons composant le noyau) avec une connexion forte à la théorie QCD
ii) la mise au point de méthodes mathématiques permettant des approximations précises et contrôlées des solutions exactes de l'équation de Schrödinger à A corps.
Il y a trois décennies, les travaux fondateurs de S. Weinberg ont ouvert la voie à une théorie systématique des interactions inter-nucléons ancrée dans la QCD. Il créa un cadre mathématique, appelé théorie effective des champs chirale (EFT), qui permet de construire des Hamiltoniens1 nucléaires systématiquement améliorables. De tels Hamiltoniens ont aujourd'hui remplacé les modèles phénoménologiques précédents et sont désormais utilisés de manière standard dans l'équation de Schrödinger à A corps. Néanmoins, trouver la solution de l'équation de Schrödinger pour une large gamme de noyaux reste un problème non trivial, tant d’un point de vue formel que d’un point de vue capacité de calcul. C'est pourquoi ces calculs se sont longtemps limités aux systèmes légers ayant un nombre de nucléons A≤12.
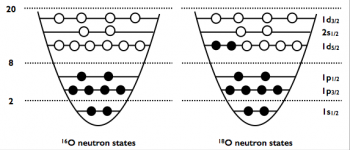
Figure 2: Les états neutroniques de 16O (double couche fermée) et 18O (simple couche ouverte) dans le cadre du modèle en couches standard sans interaction. Les cercles remplis (ouverts) correspondent aux états occupés (inoccupés) dans l'état de référence. Ici l’oxygène est considéré fermé en proton (Z=8).
Vers la solution exacte
Au cours des 15 dernières années, des méthodes mathématiques ont été mises au point pour construire la solution exacte en partant d’un état de référence de champ moyen et ont ainsi permis de décrire des noyaux plus lourds jusqu'aux isotopes d'étain (Z = 50). Cependant, ces méthodes sont restées limitées jusqu'à récemment aux noyaux ayant un nombre spécifique de protons et de neutrons : les noyaux dits à « double couche fermée ». En effet, en première approximation, un noyau peut être décrit par un état obtenu en remplissant des protons et des neutrons sur deux ensembles de couches, chaque couche ne pouvant accepter qu'un nombre spécifique de nucléons. Lorsque les nombres de protons et de neutrons sont tels que leurs couches supérieures sont entièrement remplies, le noyau correspondant est dit à " double couche fermée " (voir Fig. 2). Ces noyaux sont relativement plus stables et plus faciles à décrire que leurs voisins car ils autorisent l'utilisation d’un déterminant standard comme état de référence : le déterminant de Slater. Ces dernières années, les théoriciens de l'Irfu/DPhN ont mis au point différents développements permettant d'effectuer des calculs ab initio pour des noyaux à simple couche ouverte, c'est-à-dire des noyaux dont la couche supérieure de protons ou de neutrons n'est pas complètement occupée, cas physiques plus difficiles à résoudre. Cela a étendu la portée des calculs ab initio de quelques dizaines à plusieurs centaines de noyaux.
Briser la symétrie de l'Hamiltonien
L'idée clé derrière ces approches est de permettre à l'état de référence de briser une symétrie de l’Hamiltonien sous-jacent. Pour les noyaux semi-magiques, la symétrie pertinente à briser est ce qu'on appelle la symétrie globale de jauge U(1), une symétrie associée au simple fait que les noyaux sont constitués de nombres spécifiques de protons et de neutrons. Dans ces approches, le système est d'abord autorisé à ne pas avoir exactement Z protons ou N neutrons afin de prendre en compte la complexité associée au caractère partiellement rempli de la couche supérieure. Cette idée conduit à l'utilisation d'un état de référence de Bogoliubov (résolution des équations champ moyen de Hartree-Fock-Bogoliubov) qui généralise l'utilisation d’un simple déterminant de Slater (solution de la célèbre théorie du champ moyen Hartree-Fock). Ceci permet de capturer le caractère superfluide des noyaux à simple couche ouverte. Bien que la brisure de symétrie U(1) soit un outil standard utilisé dans les calculs de type champs moyens, elle n'avait jamais été appliquée aux méthodes au-delà du champ moyen, c’est-à-dire aux méthodes qui visent à établir une solution précise de l'équation de Schrödinger à A corps et permettent ainsi des calculs ab initio des propriétés du noyau atomique. Le formalisme développé récemment par les théoriciens de l'Irfu/DPhN consiste en un développement perturbatif autour de l'état de référence de Bogoliubov et brisant la conservation du nombre de protons ou de neutrons, il est donc appelé théorie des perturbations pour le problème à N corps de Bogoliubov (BMBPT). En Fig. 3, une comparaison systématique des résultats du BMBPT avec d'autres méthodes de pointe, dont l'une a également été développée par le même groupe [ADC(2)], est présentée pour trois chaînes isotopiques différentes. S'il est évident que le BMBPT est extrêmement performant en comparaison des méthodes existantes, tant pour les énergies de liaison que pour les énergies de séparation à deux neutrons, il l'est avec un temps de calcul réduit de deux ordres de grandeur. Cela fait du BMBPT un candidat extrêmement performant pour effectuer des calculs globaux à grande échelle sur l'ensemble de la carte des noyaux, ce qui permet de tester en profondeur les Hamiltoniens nucléaires de prochaine génération. De plus, les futurs développements concernant des noyaux à double couche ouverte, qui constituent un réel défi, seront beaucoup plus simples à réaliser que dans d'autres cadres.
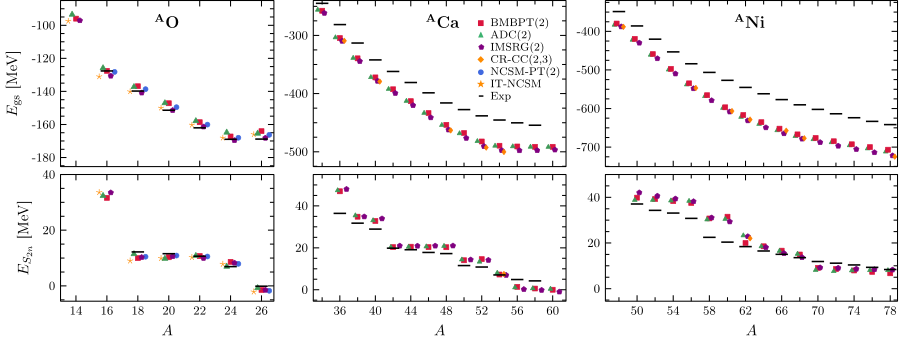
En résumé, les théoriciens de l'Irfu/DPhN ont ajouté une nouvelle méthode ab initio pour résoudre le problème à N corps, dédiée à la description des noyaux de masse intermédiaire à couches ouvertes. Cette méthode concurrence toutes les méthodes précédemment disponibles, tout en ayant un coût de calcul beaucoup plus faible. Presque entièrement développée à l'Irfu/DPhN, cette nouvelle méthode marque l'importance croissante du groupe théorique du CEA dans le secteur des théories ab initio pour la structure nucléaire.
1] A. Tichai, P. Arthuis, T. Duguet, H. Hergert, V. Somà, R. Roth, Phys. Lett. B786 (2018) 195
Contact : Alexander TICHAI CEA-Saclay/Irfu/DPhN/LENA
1. Hamiltonien : opérateur mathématique décrivant la dynamique des particules en interaction. Dans le cas de l’Hamiltonien nucléaire, il s'écrit comme la somme des énergies cinétiques des A nucléons et la somme des interactions à deux corps, trois corps, ... entre les nucléons. Contrairement aux cas plus simples, comme la répulsion Coulombienne en électromagnétisme, il n’existe pas de forme analytique du potentiel - en termes de degrés de liberté spatial, de spin et d'isospin - pour l’interaction forte.



