Depuis 2010 la question de la taille du proton est au cœur d’une controverse entre physiciens atomistes et physiciens hadroniques. En effet, des mesures très précises de physique atomique ont conclu à une taille du proton beaucoup plus petite que ce qui était attendu, en très fort désaccord avec les expériences de diffusion élastique. En collaboration avec l'Université de Pérouse, une physicienne de l’Irfu a mené l’enquête pour trouver le responsable d’une telle différence. Les résultats ont été publiés dans European Journal of Physics A [3].
La métrologie est la science qui vise à mesurer, avec la plus grande précision possible, les constantes de la physique et à définir des étalons pour leur mesure. Ainsi, par exemple, on définit depuis 1983 le mètre comme la distance parcourue dans le vide par la lumière pendant 1/299.792.458 de seconde. Cette définition du mètre est très générale car elle s'appuie sur l'invariance de la vitesse de la lumière perçue par différents observateurs situés dans des référentiels Galiléens. En retour, cette définition utilise notre connaissance de la vitesse de la lumière, forcément limitée par la précision des instruments de sa mesure et donc imparfaite.
Deux mesures, deux tailles du proton
De la même manière, la connaissance précise de la taille du proton (d'environ 1 fm) est extrêmement importante car cette particule est à la fois la plus stable connue (sa période de désintégration est de plus de 1029 ans) mais constitue de plus, en ce qu'elle est le noyau de l'atome d'hydrogène, l'élément le plus abondant de l'univers. Pourtant, cette taille est au cœur de vives polémiques car elle ne peut être mesurée directement, et nécessite par conséquent d’être extraite via différentes grandeurs intermédiaires accessibles à la mesure. Le problème concernant la taille du proton est que ces extractions mènent à des conclusions différentes !
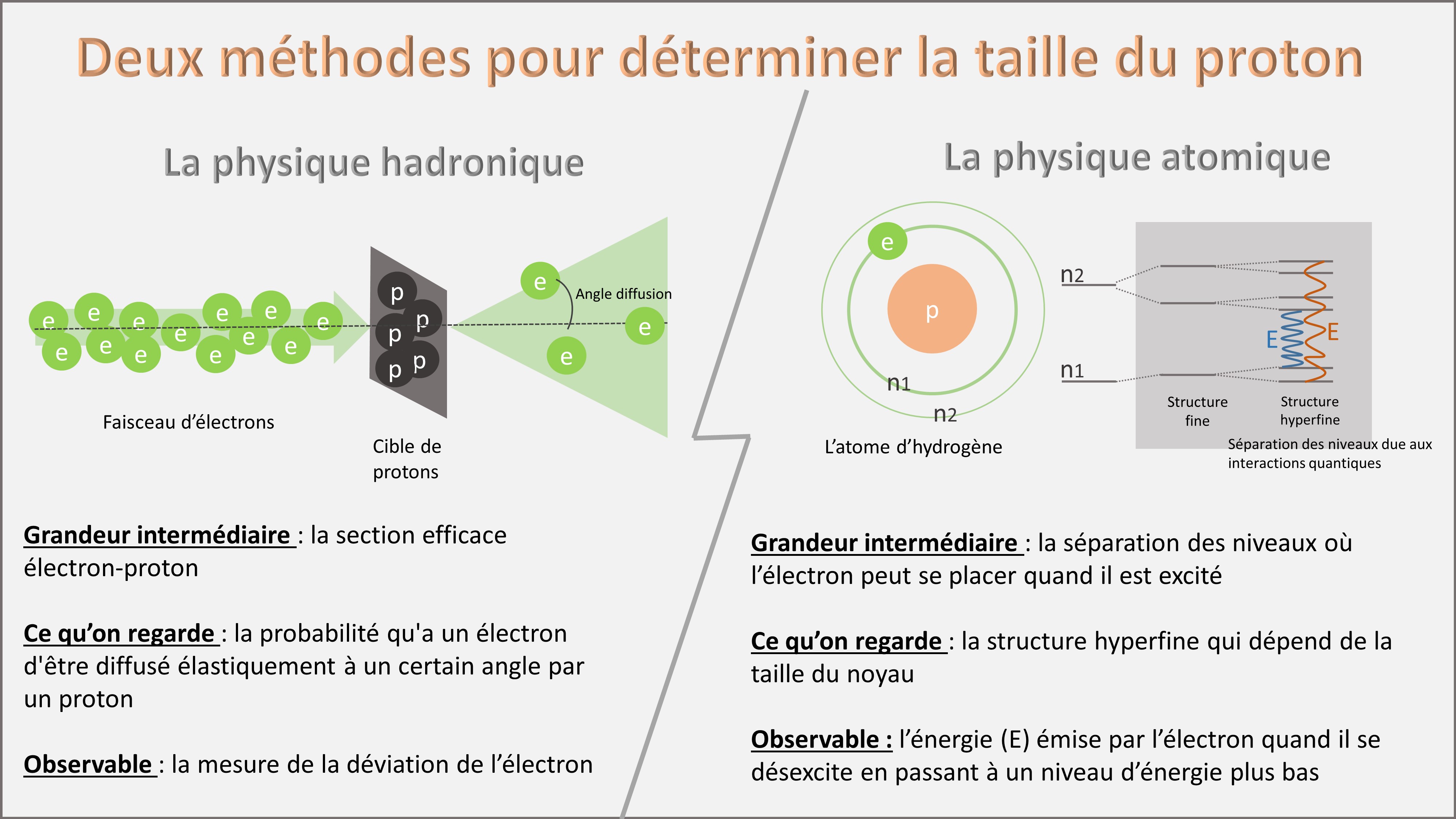
proton. La physique hadronique utilise la section efficace électron-proton
alors que la physique atomique s'intéresse à l'influence de la taille du proton
sur les niveaux électroniques.
Ainsi, la communauté des physiciens hadroniciens utilise comme grandeur intermédiaire la mesure de la section efficace élastique électron-proton, c'est à dire la probabilité qu'a un électron d'être diffusé élastiquement à un certain angle par un proton (cf figure 1, gauche) et en déduisent la taille du proton. Les résultats de la diffusion élastique dépendent de la distribution de la charge, donc la taille de la cible vue par l’électron pendant l’interaction. On peut ainsi déduire la taille du proton.
La communauté de la physique atomique utilise quant à elle la séparation de niveaux électroniques dans l’atome d’hydrogène (structure hyperfine de l’atome, domaine de la physique atomique). En effet chaque niveau électronique se sépare en sous-structure à cause de perturbations quantiques, c’est la séparation ‘hyperfine des états quantiques’ de l’hydrogène. Les électrons ne peuvent occuper que ces niveaux définis en fonction de leur énergie. L’énergie émise par l’électron lorsqu’il change de niveaux (E sur la figure) contient un terme correctif qui dépend de la distance de l’orbite avec le cœur de l’atome, le proton.
Jusqu'en 2010, les mesures réalisées par les deux communautés étaient en accord : le Committee on Data for Science and Technology (CODATA) enregistrait une valeur de taille de proton mesurée rpe =0.8775±0.0051 fm issue de la physique atomique en accord avec les résultats de diffusion élastique rpel=0.886±0.008 fm, affectée cependant d’une plus grande incertitude [1].
En faisant orbiter autour du proton non pas un électron mais un muon, 200 fois plus lourd que l'électron, des physiciens atomiques ont remis cet accord en cause : sous l'effet du poids du muon, l’hydrogène muonique est beaucoup plus compact et le muon, en orbite rapprochée autour du noyau, ressent alors bien plus fortement la charge du proton. Les termes correctifs aux orbites deviennent plus importants et permettent une détermination très précise de la taille du proton donnée par rpm=0.84087±0.00039 fm. Il semblerait donc que le proton soit bien plus mince que ce qui était admis [2], d'autant que cette mesure est affectée d'une précision bien plus grande que les précédentes !
Les expériences et les études théoriques se sont alors succédées : dans le camp de la physique atomique, en mesurant différentes transitions (c’est-à-dire l'énergie émise par l'atome lorsque l'électron ou le muon passe d'un niveau à un autre) avec des atomes électroniques et muoniques, et dans celui de la physique hadronique en réalisant des expériences de plus en plus précises, dans des conditions cinématiques où l’électron perturbe le moins possible le proton.
Les résultats sont, à ce jour, incohérents, certaines expériences confirmant un proton mince, d’autres un proton gros, et ceci dans les deux camps. Une théoricienne de l'Irfu, en collaboration avec un collègue de l'Université de Pérouse, a alors décidé de mener une analyse critique du formalisme théorique permettant de réaliser les mesures de section efficace pour accéder à la taille du proton à l'aide de la physique hadronique. Cette étude, publiée par EPJA [3] invalide l'ensemble des résultats obtenus par diffusion élastique au-delà d'une certaine précision en mettant à jour un biais fort affectant les analyses.
Diffusion élastique & erreur systématique
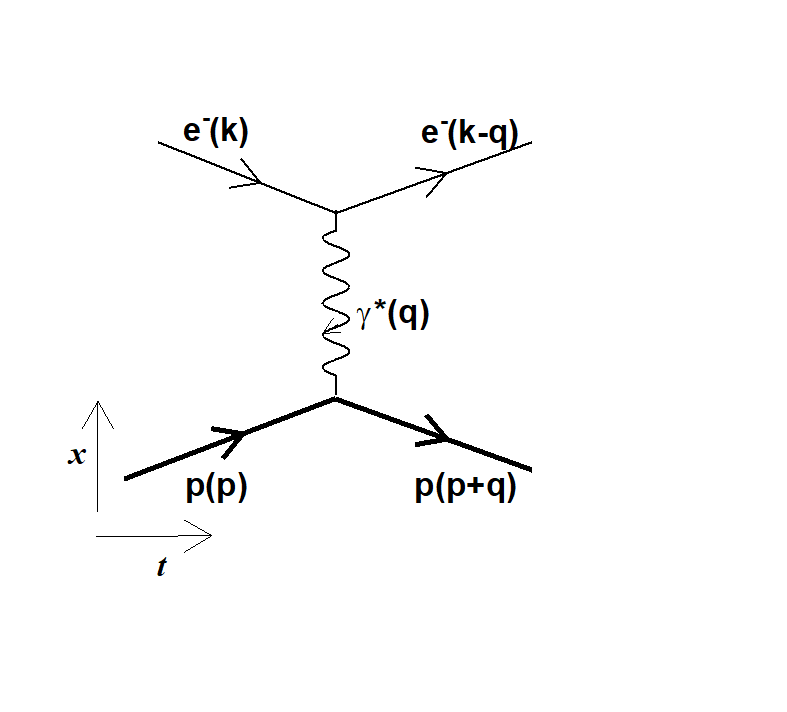
Figure 2 : la diffusion élastique entre l'électron (e-) et le proton (p) implique l'échange d'un photon dit virtuel (?*).
En effet la diffusion élastique d'électrons sur un proton implique l’échange d’un photon dit virtuel, qu’on caractérise par ‘q2’, le carré du quadri moment énergie-impulsion, grandeur transférée de l’électron au proton (fig 2). La méthode pour extraire le rayon du proton requiert la mesure de la section efficace élastique électron-proton, aux plus basses valeurs de q2. Cette valeur pour la diffusion élastique est finie et l’expérience vise à mesurer le plus précisément possible les sections efficaces aux plus petites valeurs de q2. Un traitement de ces résultats permet de remonter au rayon du proton.
La section efficace s’exprime en termes de ‘facteurs de forme ’, quantités qui paramétrisent les distributions de charge et magnétique. Le rayon est ensuite défini comme la limite pour q2->0 de la dérivée du facteur de forme de charge, qui est dominant et qui est normalisé à la valeur de la charge élémentaire (l’unité) à q2=0.
Or, en réanalysant les données les plus récentes et les plus précises des expériences des collaborations A1 à Mayence [4], et PRad à JLab [5], (Fig. 3) l'équipe franco-italienne a montré que la valeur obtenue par l’extrapolation de la section efficace dépend de l’intervalle de q2 où sont sélectionnées les données ainsi que de la fonction prédéfinie utilisée pour le fit des données. Les fluctuations sur les valeurs reconstruites du rayon sont d'autant plus importantes que la borne inférieure en q2 de l'intervalle d'ajustement est faible.
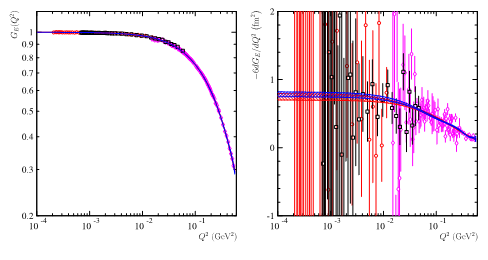
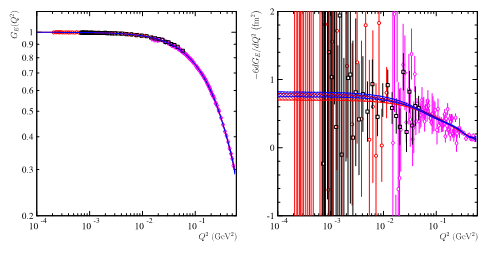
Fig. 3 : Données de CLAS [5] à q2=1.1 GeV2 (cercles rouges) et q2=2.2 GeV2(carrés noirs) et Mainz [4] (losanges roses), à gauche le facteur de forme électrique, à droite sa dérivée numérique, qui, multipliée par -6, donne directement la valeur du rayon. Les courbes bleu et rouges donnent les surfaces les plus probables obtenues à l'aide de deux ajustements par des polynômes de degré 7 (d'une variable réelle (courbe bleue), et l’autre extrapolée dans le plan complexe (courbe rouge)).
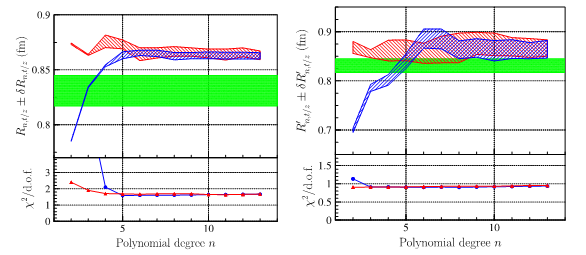
Fig.4 : Rayon extrait par les deux différentes paramétrisations, en fonction du degré du polynôme, à gauche par un fit sur le facteur de forme, à droite par le fit sur la dérivée numérique. La bande verte représente le résultat publié par l’expérience JLab-PRad. Le cadre inférieur représente ‘la bonté du fit’ : on note sa stabilité au-dessus du degré 5 pour le rayon, et du degré 3 pour la dérivée.
En particulier, ces valeurs reconstruites à partir de différentes fonctions de fit (Fig. 4) font apparaitre des erreurs numériques sur la dérivée (proportionnelle au rayon) bien plus importantes que les erreurs affichées par les expériences. Cette erreur systématique entachant la valeur reconstruite du rayon finit par devenir bien plus grande que l'erreur attribuée à la mesure de la section efficace, et traduit un problème conceptuel : le rayon n’est pas mesuré mais extrait d’une grandeur intermédiaire, elle-même extrapolée ! (via le formalisme du système de particules en interaction pour le traitement de la diffusion à deux corps). Or, lorsque l'électron s'approche du proton pour en sonder la taille, le système devient lié et la limite q 2=0 est obtenue si l’angle ou l’énergie de l’électron émis sont nuls. Dans le premier cas l’électron est émis à zéro degré et par conséquent ‘ne voit pas’ la cible. Dans le deuxième cas, l’électron n’est pas émis et est capturé par le proton, ce qui interdit d'utiliser un formalisme à deux corps puisque le système résultant est un noyau composé.
Peut-on dépasser ces problèmes d’extrapolation ? Rien n’est moins sûr car l’extraction du rayon repose sur un mécanisme physique de diffusion à deux corps (ici le proton et l’électron). Or, si l’énergie de l’électron devient trop faible, ce dernier est capturé par le proton, formant ainsi un état lié d’hydrogène qui devient alors un problème à un corps. Le phénomène de diffusion s’arrête, et prive les physiciens de données supplémentaires pour extraire le rayon du proton.
Ainsi, l’équipe franco-italienne conclut que la diffusion élastique ne peut être considérée une méthode précise pour déduire le rayon carré moyen d’une particule, qui est une propriété statique. La balle est désormais dans le camp de la physique atomique !
Références :
[1] The NITS Reference on Constants, Units, and Uncertaity. https://
physics.nist.gov/cgi-bin/cuu/Value?rp|search_for=proton+rms
[2] R. Pohl et al., Nature 466, 213 (2010)
[3] S. Pacetti and E. Tomasi-Gustafsson, Eur. Phys. J. A57 (2021) 72 et Eur.Phys. J. A56 (2020) 3.
[4] J.C. Bernauer et al. (A1 Collaboration), Phys. Rev. C 90, 015206 ( 2014)
[5] W. Xiong et al., Nature 575, 147 (2019).
Contact :
• Structure de la matière nucléaire › Noyaux atomiques