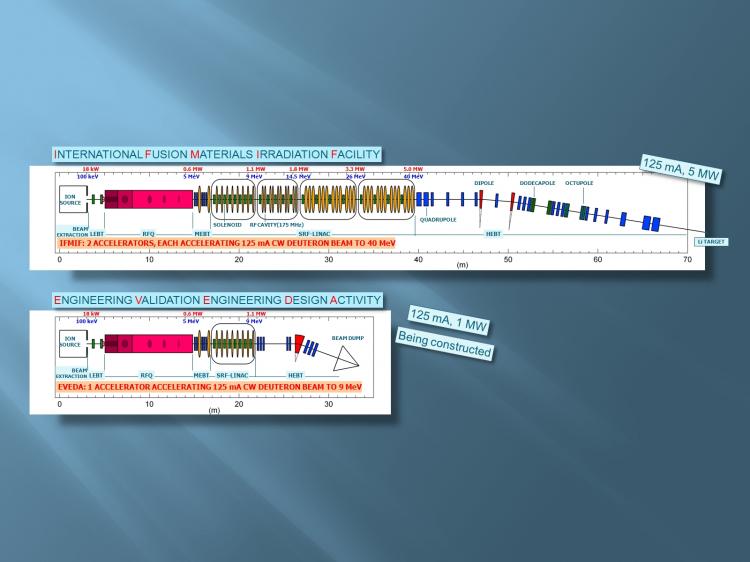
Synoptique des accélérateurs d'IFMIF-EVEDA. Les sections successives sont: Extraction, LEBT (Low Energy Beam Transport), RFQ (Radio-Frequency Quadrupole), MEBT (Mean Energy Beam Transport), SRF-Linac (Superconducting Radio-Frequency Linear Accelerator) et HEBT (High Energy Beam Transport). L'énergie et la puissance du faisceau de particules (D+) sont données à la sortie de chaque section.
Les missions de la Dynamique du Faisceau
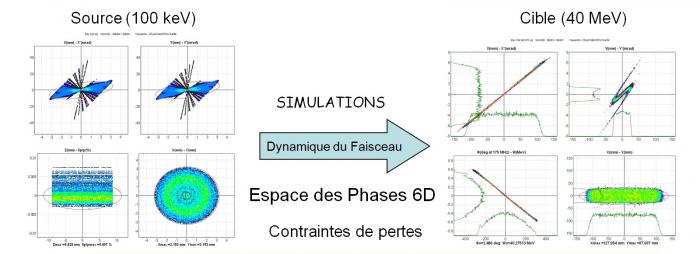
Il s'agit de définir et optimiser tous les paramètres physiques (configurations de champ électrique et magnétique) de l'accélérateur, permettant de conduire le faisceau de particules représenté par son espace de phase à 6 dimensions, de la source à la cible selon les performances requises tout en respectant les contraintes de pertes imposées.
Cela revient à définir les performances et les tolérances de tous les éléments entourant le faisceau: dipôles, quadrupôles, solénoïdes, RFQ, cavités RF, correcteurs, chambre à vide, collimateurs, moyens de mesure faisceau.
L'objectif in fine est d'obtenir un modèle théorique le plus réaliste possible de l'accélérateur, à partir duquel l'accélérateur va être piloté. Pour arriver à cette fin, le travail du "dynamicien" repose sur trois volets:
- simulations massives à des fins d'optimisation et de design de paramètres
- interactions intenses avec toutes les équipes de design technique et de fabrication des composants de l'accélérateur
- définition et conduite des expérimentations avec faisceau sur l'accélérateur.
Les Défis d'IFMIF-EVEDA
Les principales difficultés proviennent des deux performances record demandées aux faisceaux d'IFMIF-EVEDA :
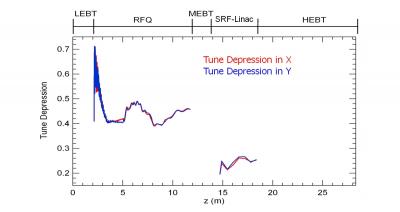
- La très haute intensité, 125 mA en continu, implique que les forces répulsives entre particules du faisceau même, appelées forces de charge d'espace, dominent complètement les forces de focalisation qui doivent être appliquées au faisceau. En effet, le facteur de Tune Depression (voir figure) est seulement de 0.4 dans le RFQ et 0.2 dans le SRF-Linac. Le contrôle total de l'ensemble des particules est donc problématique.
- La très grande puissance, 1 à 5 MW, implique que les pertes faisceau, même minimes, sont dangereuses pour les matériels. Le problème devient encore plus critique au-delà de l'énergie de 5 MeV, c.-à-d. à la sortie du RFQ, où l'activation des matériels commence à être préoccupante. Il faut alors limiter les pertes à bien moins qu' 1 millionième du faisceau.
Surmonter ces deux difficultés séparément représente déjà deux défis en soi. Les cumuler entraîne un degré de difficulté supérieur. D'un côté, l'importante charge d'espace rend les pertes erratiques difficilement contrôlables. De l'autre, c'est pratiquement le niveau de zéro perte qui est requis.
La stratégie adoptée
Pour éviter l'explosion du faisceau sous les forces de charge d'espace, il faut réduire au minimum l'espace entre les éléments focalisants. Mais cela empêche aussi l'installation des moyens de mesure du faisceau qui sont particulièrement indispensables dans le cas présent.
En effet, qui dit forte charge d'espace, dit aussi calculs fortement non-linéaires dont le réalisme ne peut être garanti à 10-6 près, précision pourtant nécessaire pour satisfaire les contraintes de pertes évoquées. Toute optimisation théorique n'a alors de sens que s'il peut être reproduit en situation réelle par un réglage fin d'après les mesures sur le faisceau.
La stratégie consiste donc à faire toutes les optimisations et réglages théoriques de telle manière qu'ils peuvent être reproduits sur la machine avec les rares moyens de mesure disponibles, ou de proposer les moyens de mesure appropriés qui permettraient de faire les réglages fins sur la machine comme ils avaient été faits théoriquement.
Difficultés et choix pour les énergies < 5 MeV
Les difficultés sont plus particulièrement liées à la haute intensité. D'une part, la prépondérance de la charge d'espace y est la plus marquée, car les particules ont encore une faible vitesse. D'autre part, il faut limiter les pertes, relativement importantes (~%), qui peuvent contrarier l'obtention de l'intensité requise de 125 mA.
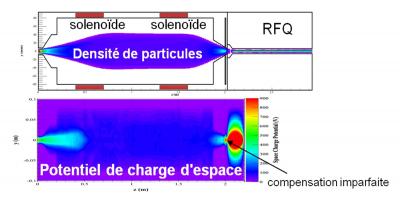
Un calcul détaillé de la carte de charge d'espace a été entrepris, tenant compte des phénomènes de compensation par les électrons créés par l'ionisation du gaz résiduel, ou refoulés par une électrode installée à l'entrée du RFQ. Le RFQ, premier composant qui accélère véritablement, a été optimisé pour que les pertes faisceau soient limitées aux particules de très faible énergie, non encore accélérées. L'ensemble LEBT + RFQ a été optimisé et réglé avec le critère de transmission maximale, méthode qui pourra être reproduite in-situ en mesurant le courant faisceau à la sortie de la source puis après le RFQ. Une transmission théorique de plus de 95% a été obtenue.
Difficultés et choix pour les énergies > 5 MeV
Les difficultés sont plus particulièrement liées à la forte puissance. A ces énergies, la puissance faisceau, de 0.6 MW à 5 MW concentrée sur quelques cm2, est préoccupante pour les composants accélérateurs, surtout pour les éléments supraconducteurs qui doivent être maintenus à quelques Kelvin, mais aussi pour l'activation des matériaux en cas de perte. Cela nécessite de limiter les pertes à bien moins que 10-6 du faisceau.
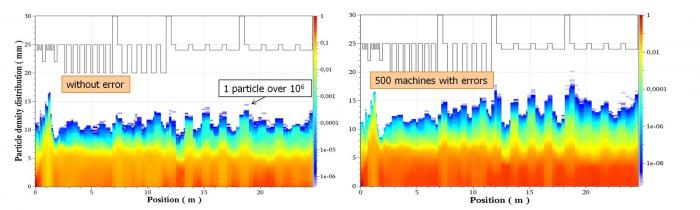
Des simulations avec plus de 106 macro-particules ont été entreprises, avec pour objectif d'éviter la perte de chacune d'entre elles. Cela contraste avec la méthode classique où l'attention est plutôt portée sur l'émittance ou l'enveloppe rms du faisceau, quantités qui non seulement ne sont pas appropriées ici mais en plus ne peuvent être mesurées dans notre situation de manque de place. On a suggéré à la place des dispositifs de mesure de micro-pertes installés au plus près de la chambre à vide des solénoïdes. Cela permettra de faire les réglages fins similaires aux simulations numériques. On a ainsi obtenu une situation de zéro perte qui se maintient même en présence des erreurs tolérées.
Contact : Phu-anh-phi NGHIEM
Contributeurs:
- CEA-France : Nicolas Chauvin, Olivier Delferrière, Romuald Duperrier, Alban Mosnier, Didier Uriot
- INFN-Italie : Michele Comunian
- CIEMAT-Espagne : Concepcion Oliver
 thpc028-EPAC08-HEBT-COliver-etal.pdf
thpc028-EPAC08-HEBT-COliver-etal.pdf
 thpc088-EPAC08-HWR-Linac-NChauvin-etal..pdf
thpc088-EPAC08-HWR-Linac-NChauvin-etal..pdf
 thpp075-EPAC08-RFQ-MComunian-etal.pdf
thpp075-EPAC08-RFQ-MComunian-etal.pdf
 mop036-LINAC08-RFQ-MComunian-etal.pdf
mop036-LINAC08-RFQ-MComunian-etal.pdf
 mop072-LINAC08-LEBT-NChauvin-etal.pdf
mop072-LINAC08-LEBT-NChauvin-etal.pdf
 mop073-LINAC08-ParamDesign-PNghiem-etal.pdf
mop073-LINAC08-ParamDesign-PNghiem-etal.pdf
 th5pfp004-PAC09-LEBT-NChauvin-etal.pdf
th5pfp004-PAC09-LEBT-NChauvin-etal.pdf
 th5pfp005-PAC09-HWR-Linac-NChauvin-etal.pdf
th5pfp005-PAC09-HWR-Linac-NChauvin-etal.pdf
 th5pfp006-PAC09-Strategies&Choices-PNghiem-etal.pdf
th5pfp006-PAC09-Strategies&Choices-PNghiem-etal.pdf
 tupea014-IPAC10-HEBT-COliver-etal.pdf
tupea014-IPAC10-HEBT-COliver-etal.pdf
 tuo1b03-HB2010-Challenges&Treatments-Nghiem.etal.pdf
tuo1b03-HB2010-Challenges&Treatments-Nghiem.etal.pdf
 mopso26-IPAC11-Start-to-End simulations-NChauvin-etal.pdf
mopso26-IPAC11-Start-to-End simulations-NChauvin-etal.pdf
 moodb01-IPAC11-IFMIFDynamics-PNghiem-etal.pdf
moodb01-IPAC11-IFMIFDynamics-PNghiem-etal.pdf
 mopso27-IPAC11-StabilityCharts-WSimeoniJr-etal.pdf
mopso27-IPAC11-StabilityCharts-WSimeoniJr-etal.pdf
 mopso25-IPAC11-EmittanceMeasurements-PNghiem-etal.pdf
mopso25-IPAC11-EmittanceMeasurements-PNghiem-etal.pdf

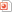 poster Beam_Dynamics.2.pptx
poster Beam_Dynamics.2.pptx