A scientist from IRFU published an article in the Physical Review A presenting a diffraction model based on the concept of quantum measurement [1]. This model represents a new approach because the amplitude of the diffracted wave is usually calculated using classical methods of wave optics. Several specific effects of the quantum aspect of the model are predicted, three of which can be the subject of experimental tests: a typical damping of the light intensity at large diffraction angles, an angular factor different from that of classical theories and a characteristic parameter of a link between the polarization and the momentum of the diffracted photons. Experiments carried out at IRAMIS in the coming months will make it possible to simultaneously measure the momentum and polarization of the detected photons and thus validate or not the proposed model.
We can observe the phenomenon of diffraction when a wave encounters material obstacles, for example, a diaphragm whose aperture is adjustable (Fig. 1).
We can consider the wave coming from the source and arriving at the aperture of the diaphragm as a plane wave whose direction of propagation is that of the Oz axis (called longitudinal direction). Diffraction occurs when the wave passes through the aperture. The incident plane wave becomes a diffracted wave that now propagates in several directions around the Oz axis with a different intensity for each direction. The value of this intensity as a function of direction (angular distribution) depends on the shape of the aperture and the wavelength.
In classical wave optics, we can calculate the amplitude of the diffracted wave by applying the Huygens-Fresnel principle according to which the wavefront located at the aperture is a set of secondary sources emitting spherical wavelets towards the region where the detectors are located. The sum of these wavelets, which interfere with each other, is equal to the diffracted wave.
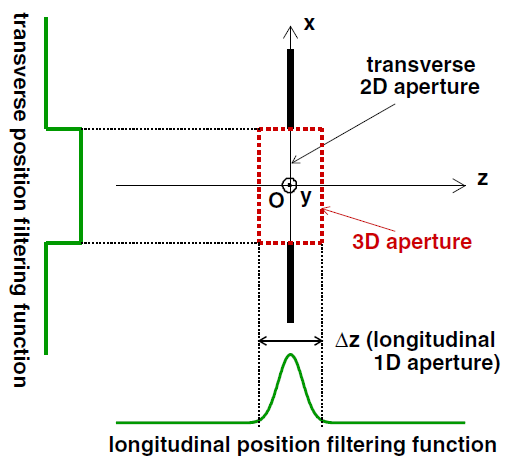
Figure 2: example of a 3D aperture (section in the x,z plane) with transverse and longitudinal filtering functions.
In quantum mechanics, the wave is associated with a particle, for example the photon in the case of light. The calculation performed in wave optics using the Huygens-Fresnel principle is equivalent to a direct calculation of the wave function of the particle but without prior calculation of its quantum state. The model presented in the recently published article [1] starts from the basic principles of quantum mechanics to calculate this quantum state and then deduce the wave function. It considers diffraction by a diaphragm as the consequence of a measurement of the position of the particle when it passes through the aperture and expresses the state that results from this position measurement. The latter includes the measurement of the transverse coordinates (x,y), with the uncertainties Δx and Δy corresponding to the size of the aperture, but also a measurement of z since the particle then crosses the plane of the diaphragm for which z = 0. However, due to quantum mechanics, this measurement of z occurs with an uncertainty Δz that is generally non-zero. The position measurement therefore causes a temporary localization of the wave function in a volume constituting a sort of three-dimensional (3D) aperture. The notion of filtering function is used to represent the localization zone relative to each coordinate (Fig. 2). The 3D aperture is formed from the transverse 2D aperture used in wave optics and from a longitudinal 1D aperture. The absence of a material edge in the longitudinal direction implies that the associated filtering function is not necessarily a rectangular function as in the case of transverse coordinates.
Three specific effects of the quantum nature of the model can be measured:
- Multi-wavefront Huygens-Fresnel principle.
Taking into account the longitudinal coordinate in the context of a 3D aperture implies that the emission of the wavelets involved in the Huygens-Fresnel principle does not occur from a single wavefront but from several neighboring wavefronts. The width Δz of the distribution of these wavefronts is a parameter of the model and can be fitted to the data from measurement of the intensity of the diffracted wave as a function of the diffraction angle. Fig. 3 presents two predictions of the quantum model (corresponding to two values of Δz) and the predictions of the three best-known classical theories of wave optics (Fresnel-Kirchhoff and Rayleigh-Sommerfeld 1 and 2) for a case of diffraction of photons through a rectangular slit.
Significant differences between the predictions appear at large diffraction angles, a region for which accurate experimental measurements are lacking. The quantum model predicts a typical damping of the intensity in this region, which is more important as Δz is large (QM2 curve). An experimental study of the Huygens-Fresnel principle can therefore be considered.
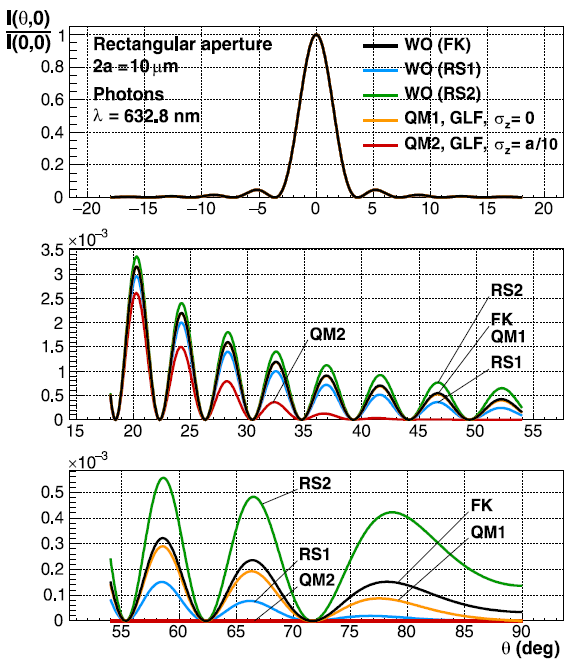
Figure 3: Comparison between five theoretical predictions of relative intensity for a photon diffraction case: three wave optics (WO) predictions corresponding to Fresnel-Kirchhoff (FK) and Rayleigh-Sommerfeld (RS1 and RS2) theories and two quantum model predictions (QM1 and QM2) where the longitudinal filtering function is a Gaussian (GLF) of standard deviation σz(Δz). The case σz = 0 corresponds to the Huygens-Fresnel principle with a single wavefront.
- Angular factor
In the quantum model, in addition to the damping related to the value of Δz, the decrease in intensity as a function of the diffraction angle depends on an angular factor different from the obliquity (or inclination) factors of wave optics theories. This factor plausibly describes the decrease in intensity to zero at the angular limit of 90° (QM1 and QM2 curves) unlike the FK and RS2 curves for which the value at 90° is generally non-zero. The RS1 curve decreases to zero but differently from the QM curves.
- Polarization
The position measurement modifies the polarization states of the particles. In the case of incident photons in an elliptically polarized pure state, the quantum model predicts that the axes of the ellipse can undergo a rotation which depends on the momentum transfer between the particle and the diaphragm and consequently on the angle of diffraction. The angle of this rotation is a parameter of the model. It can be fitted to the data from measurement of polarization of the detected photons.
Experiments to test the quantum model are currently being prepared at IRAMIS/SPEC/LEPO (F. Charra, L. Douillard, C. Fiorini, S. Vassant). The experimental setup will make it possible to reach a maximum angle of 75° and to carry out the simultaneous measurement of the momentum and polarization of the detected photons.
References:
[1] B. Fabbro, “Position measurement and the Huygens-Fresnel principle: A quantum model of Fraunhofer diffraction for polarized pure states”, Phys. Rev. A 107, 033706 (2023) (https://doi.org/10.1103/PhysRevA.107.033706).
Contact: Bernard Fabbro
• Modelisation, calculation and data analysis › Modeling and visualization methods
• Institute of Research into the Fundamental Laws of the Universe • The Particle Physics Division