Du point de vue de la modélisation mathématique, rien ne ressemble plus à une épidémie... qu'un réacteur nucléaire ! Si le lien entre ces deux "objets" ne tombe pas a priori sous le sens, tous deux ont en commun d'impliquer le déplacement quasi-aléatoire d'une espèce à même de se reproduire et de disparaître. Dans le cas d'une épidémie, cette espèce est l'individu infecté qui, au gré de ses déplacements, peut à son tour infecter d'autres individus. Une fois guéri (ou plus malheureusement décédé) le porteur du virus disparaît et n'influe plus sur la propagation de l'épidémie. De la même manière, mais en 3 dimensions plutôt qu'en 2, les neutrons dans un réacteur nucléaire se déplacent aléatoirement et peuvent donner naissance à d'autres neutrons, par le mécanisme de fission induite sur des noyaux lourds (comme l'uranium 235). En s'échappant du réacteur ou par capture lors de leur transport dans des milieux neutrophages, les neutrons disparaissent également et ne contribuent plus à la réaction en chaîne ayant lieu dans le cœur.
Vue de loin, la marche aléatoire des neutrons suit un mouvement Brownien, en ce qu'elle obéit à l'équation de la diffusion. Les trajectoires caractéristiques sont erratiques et bruitées (voir Figure 1.a) : les mathématiciens les qualifient de continues en tous points mais dérivables nulle part. Les réacteurs nucléaires de puissance sont d'ailleurs pilotés à l'aide de cette équation (pour être plus précis à l'aide de l'équation de la diffusion à deux groupes d'énergies : une équation pour décrire le transport des neutrons rapides, et une autre pour les neutrons plus lents, dits thermiques). Dans ce cadre, le comportement de la population des neutrons dans un réacteur est ainsi très fidèlement modélisé.
Cependant, quand la puissance dans le réacteur est stationnaire, l'étude de la réaction en chaîne s'avère plus délicate. On qualifie la diffusion des neutrons de "critique" car dans ces conditions un neutron donne précisément naissance, en moyenne, à un autre neutron au cours de sa vie, mais chaque interaction d'un neutron avec un noyau lourd peut potentiellement donner naissance à plusieurs neutrons "fils", occasionnant un branchement des trajectoires. L'étude du mouvement Brownien branchant (abrégé BBM en anglais), représenté Figure 1.b, ayant permis il y a quelques années de comprendre la phase d'amorce des épidémies [1], des modèles similaires ont alors été utilisés en neutronique pour caractériser les fluctuations statistiques du gaz de neutrons. Celles-ci peuvent se développer au point que ce dernier ne suit plus du tout les mêmes lois que celle de la diffusion simple : on parle de transition de phase. Dans cette "phase" en effet, la population totale des neutrons peut, en théorie, s'éteindre ou devenir bien plus grande que prévue et donner ipso facto lieu à une augmentation non négligeable de la puissance du réacteur. En théorie seulement, car en pratique, des travaux récents ont montré que le nombre total de neutrons dans le réacteur fluctuait très peu [2,3]. Cette surprenante stabilité trouve son origine dans l'effet de température : plus la puissance (ie le nombre de neutrons) est localement élevée, plus la température est élevée, et plus les neutrons ont tendance à être capturés par le milieu plutôt qu'à induire des fissions. Cette contre réaction est due à l'élargissement des résonances neutroniques qui deviennent littéralement des pièges à neutrons.
Cette contre-réaction, dite de Doppler Broadening, est salvatrice en ce qu'elle stabilise les réacteurs nucléaires dans le régime de puissance. En contrepartie, la modélisation théorique de ces effets devient extrêmement délicate, voire impossible : l'utilisation de codes numériques couplant la résolution des équations du transport des neutrons et à celle des équations de contre réactions en température devient incontournable. Mais ces méthodes numériques font elles même des hypothèses dont il est difficile d'apprécier la légitimité...
Afin tout de même de tenter de décrire ce phénomène, trois chercheurs d'une équipe mixte CEA-IRSN ont remarqué que le gaz de neutrons au point critique (quand la réaction en chaîne est stable) possédait exactement les mêmes propriétés de symétrie qu'un liquide filtré par une structure poreuse, comme l'eau à travers le café moulu dans les cafetières à percolation. En fait, il a été possible de montrer que les trajectoires des neutrons au point de transition de phase possédaient une invariance d'échelle spatiale caractéristique des processus stochastiques appartenant à la classe d'universalité de la percolation dirigée (dans le temps). Ainsi, les fluctuations spatiales et temporelles du champ de neutrons dans le réacteur, d'importance pour la sûreté nucléaire, pouvaient être calculées théoriquement en utilisant les méthodes de renormalisation (des résultats établis de longue date dans le cadre de la théorie quantique des champs).
Les résultats de leurs travaux, publiés dans la revue Physical Review E [4], ont fait apparaître des conclusions relativement surprenantes : l'équation de la diffusion critique caractérisant la population neutronique devient, en présence de contre réactions, une équation dite de super-diffusion, où le terme diffusif habituellement donné par une dérivée spatiale d'ordre 2 en espace prend alors une valeur non-entière , légèrement inférieure à 2! Le générateur microscopique de cette équation (qui décrit les lois du transport des neutrons) n'est plus un mouvement Brownien mais une marche aléatoire de Lévy : les trajectoires semblent très proches de celles du mouvement Brownien à l'exception de certains "sauts" projetant les neutrons à distance de leur position initiale (voir Figure 1.c). Ainsi, la distribution spatiale de la puissance dans le réacteur est légèrement modifiée (de quelques pourcents), comme indiqué par la Figure 2 où le résultat de la super-diffusion apparaît en pointillés et est comparé à celui de la diffusion simple. A peu près du même ordre de grandeur que la précision attendue des codes de calculs utilisés dans les contextes d'étude de sûreté nucléaire... Il semble donc que la balle de la sûreté soit à présent dans le camp des numériciens !
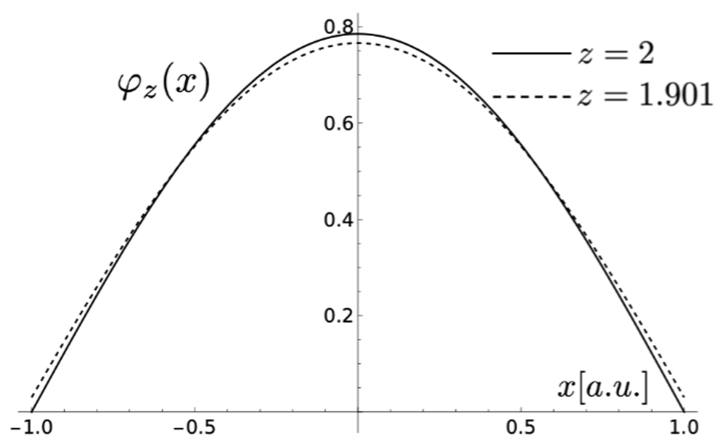
Distribution spatiale (selon l'axe x) de la population neutronique dans un réacteur simplifié, situé symboliquement entre -1 et 1. Courbe en trait plein : transport des neutrons par un modèle de diffusion classique (dérivée en espace d'ordre 2). Courbe en pointillés : transport des neutrons par un modèle de super-diffusion donné par une dérivée fractionnaire en espace d'ordre 1.901.
[1] Eric Dumonteil, Satya Majumdar, Alberto Rosso and Andrea Zoia, "Spatial extent of an outbreak in animal epidemics", PNAS 110 (11) 4239-4244 (2014) https://doi.org/10.1073/pnas.1213237110
[2] Fait marquant CEA 2022 "Rencontre entre la physique des réacteurs et la théorie des jeux" https://irfu.cea.fr/Phocea/Vie_des_labos/Ast/ast_visu.php?id_ast=4955
[3] Eric Dumonteil et al, "Patchy nuclear chain reactions", Nature Communications Physics volume 4, Article number: 151 (2021)
[4] Benjamin Dechenaux, Thomas Delcambre and Eric Dumonteil, "Percolation properties of the neutron population in nuclear reactors", Phys. Rev. E 106, 064126 (2023) https://arxiv.org/pdf/2210.02413.pdf
• Modélisation, calcul, analyse des données
• Institut de recherche sur les lois fondamentales de l'Univers (Irfu) • Le Département de Physique Nucléaire (DPhN)
• Laboratoire d'études et d'applications des réactions nucléaires (LEARN)
