Les météorites sont bombardées tout au long de leur voyage par le rayonnement cosmique. Cette irradiation est un formidable révélateur de leur histoire, à condition bien sûr de savoir la décrypter. L'interaction du rayonnement cosmique avec les noyaux atomiques constituant la météorite va produire des isotopes dits cosmogéniques, très souvent radioactifs. Des mesures d'activités, une fois la météorite trouvée sur terre, associées à un modèle peuvent permettre de remonter à sa taille pré-atmosphérique, à son temps d'exposition au rayonnement, à son âge terrestre, voire aussi à mieux connaître ce flux de rayonnement cosmique. Ce type de modèle repose sur un ingrédient clé : les sections efficaces élémentaires de production des isotopes. Ces dernières ont pour la première fois été fournies intégralement par le code de réaction nucléaire INCL développé à l’Irfu dans le cadre d’une étude des météorites ferreuses [1], augmentant ainsi la précision des analyses.
Modèle pour décrypter l'histoire des météorites
Les météorites sont des corps initialement enfouis dans des astéroïdes et qui s'en trouvent éjectés lors de collisions. Au sein de l'astéroïde, la météorite est écrantée du rayonnement cosmique, mais une fois éjectée elle le subit tout au long de son périple jusqu'à son arrivée sur terre, où l'air, l'eau, la glace, suivant où elle tombera, la protégeront là encore du rayonnement. Cette irradiation va produire nombre d'isotopes, dont les quantités dépendent de nombreux paramètres, comme le rayon pré-atmosphérique de la météorite, la concentration d’éléments à l’origine de l’isotope, le flux (φ) de rayons cosmiques, et la probabilité que ces deux derniers réagissent entre eux pour former un isotope. Cette probabilité est appelée section efficace de production (σ).
Pour arriver à tirer le maximum d'informations sur l’histoire des météorites, il faut être capable de mesurer parfois des quantités infimes d'isotopes, nécessitant une préparation délicate des échantillons et des mesures fines. Les flux (φ) sont tirés de notre connaissance du spectre du rayonnement cosmique mesuré, mais aussi de codes de calcul. En effet, ces particules sont, d'une part, ralenties dans la météorite et produisent, d'autre part, des particules secondaires, principalement des neutrons, générant à leur tour des noyaux cosmogéniques. De la même manière, les sections efficaces de production (σ) ont longtemps été tirées de mesures expérimentales. Malheureusement, ces dernières présentent des lacunes. Il faut alors systématiser les interpolations et extrapolations [2] pour couvrir tout le spectre en énergie. En parallèle, ces dernières années, la qualité des codes de réaction nucléaire s’est fortement améliorée, leur permettant maintenant de fournir des sections efficaces σ fiables et en tout point du spectre. Ceci est illustré dans une étude récente [2], démontrant l'utilité des codes de réactions nucléaire dans l’étude des météorites.
Météorites ferreuses : les avantages des isotopes 53Mn et 60Fe
Par rapport aux autres météorites, celles dites ferreuses présentent deux isotopes intéressants à prendre en compte, le 53Mn et le 60Fe. Ces deux isotopes ont des avantages certains. Tout d’abord, ayant des temps de vie plus longs que la plupart des autres isotopes, ils sont moins affectés par le temps de résidence sur terre. De plus, ils présentent des mécanismes de production simples car peu nombreux. Ainsi, les incertitudes associées aux modèles sont plus faibles. Enfin, les nouvelles techniques expérimentales (procédure de séparation chimique et mesures en spectrométrie de masse (AMS) [1]) permettent de surmonter les difficultés expérimentales (contamination, faible présence, etc.) et d’en mesurer la concentration.
Déchiffrement par combinaisons calcul-mesure
Comme mentionné plus haut, nombre d'informations sont contenues dans les taux de production des isotopes cosmogéniques. Leurs études permettent de remonter aux caractéristiques des météorites (taille...), mais également de déduire les phénomènes auxquels elles ont été exposées (collisions...).
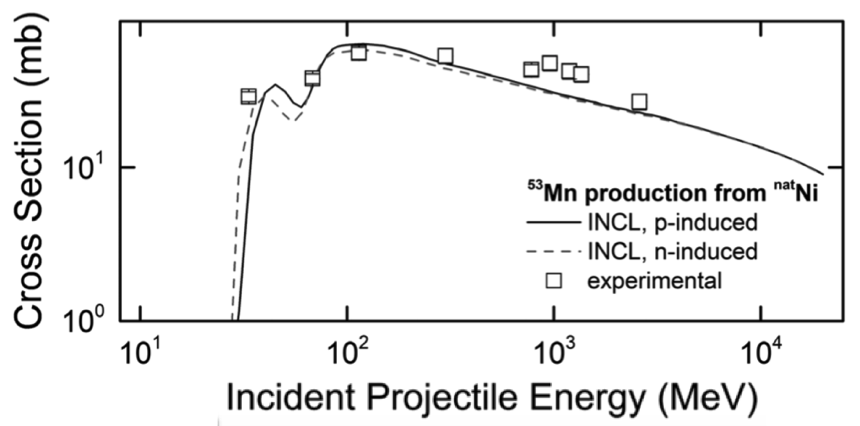
Figure 1 : Section efficace de production de 53Mn par les réactions p+ natNi et n+natNi. Les points expérimentaux ne concernent que la réaction p+natNi.
Intérêt de l'utilisation d'INCL
Parmi les ingrédients nécessaires, les sections efficaces de production des noyaux cosmogéniques restaient entachées parfois de grandes incertitudes dues par exemple aux désaccords entre différents lots de données, à une couverture partielle en énergie, ou à des lacunes concernant les particules secondaires. Certains codes de réaction nucléaire peuvent enfin pallier ces défauts, grâce aux conséquentes améliorations apportées ces dernières années. C'est pour cette raison que l'étude présentée ici s'est faite en remplaçant les extrapolations et interpolations des données expérimentales de sections efficaces par les résultats de calcul du code INCL, reconnu comme l'un des meilleurs pour simuler la production de noyaux lorsqu'il est associé au code de désexcitation Abla (cf FM du 30 janvier 2013). La Fig. 1 donne un exemple de la qualité de simulation de la production de 53Mn à partir de l'interaction d'un proton sur du Ni, mais aussi la régularité sur l'ensemble de la gamme en énergie contrairement aux données expérimentales.
Activités
La mesure de l’activité du 53Mn a été réalisée sur 46 échantillons. Les comparaisons avec les activités calculées sont très encourageantes. Ainsi, seulement huit échantillons présentent des activités supérieures aux calculs pour des tailles de météorites communément admises. Parmi les autres, citons le bel exemple de la météorite Grant. Là où les derniers résultats expérimentaux [1] indiquent une activité de 441±45 désintégrations par minute et par kilogramme (dpm kg-1), le modèle utilisant INCL donne une valeur en parfait accord, comprise entre 331 et 478 dpm kg-1 pour un rayon de 40cm environ.
En revanche, dans le cas particulier de cette météorite, les activités mesurées et calculées de 60Fe semblent pointer une taille supérieure à 1 m, ce qui n'est pas possible puisque toutes les études, dont la notre avec le 53Mn, concourent à un rayon d'environ 40cm. Une explication est peut-être à rechercher du côté des sections efficaces élémentaires de production du 60Fe. En effet, INCL prédit une prépondérance du canal n+Ni --> 60Fe, qui ne peut être testée par manque de données. Une surestimation de ce dernier pourrait expliquer la différence modèle/données. Pour l'évaluer, des techniques d'inférences bayésiennes permettant de combiner différentes sources d'information (expériences, modèles) pour accroître les connaissances devraient être mises en place à l'avenir.
Corrélations isotopiques
Les corrélations entre les activités spécifiques de deux isotopes peuvent permettre de tester la cohérence des résultats et d'émettre, sinon, des hypothèses pour expliquer des comportements non prévus par le modèle. Par exemple, l'activité du 53Mn en fonction de celle du 36Cl nous aide à comprendre l'histoire d'exposition des météorites au rayonnement cosmique.
La Fig. 2 montre cette corrélation. Si dans 25 cas les calculs et les mesures sont cohérents, 10 cas méritent une explication. Par exemple, il y a cinq météorites (Casas Grandes, Sikhote-Alin, Calico Rock, Schwetz, Trenton) pour qui les mesures individuelles de 36Cl [4] et de 53Mn [1] correspondent à des valeurs calculées pour les tailles les plus courantes, mais pour qui les corrélations sont en dehors des prévisions du modèles. Les conclusions d'autres études sur le 36Cl poussent à penser que c’est l’activité du 53Mn qui est anormalement élevée. Deux explications sont alors possibles : ou des problèmes sont survenus pendant la préparation des échantillons et/ou des mesures AMS, ou l'histoire de l'exposition est complexe. Habituellement, on suppose que la météorite est exposée au rayonnement cosmique en continu entre son éjection de l'astéroïde et son arrivée sur terre. Or elle peut aussi subir une ou des collisions, compliquant de beaucoup l'analyse du lien entre les activités de différents isotopes. Les pertes de matière exposent ainsi des couches plus profondes, modifiant les taux de production et les corrélations. Si cette explication est recevable pour certaines météorites, malheureusement, elle ne tient pas, par exemple, pour la météorite Calico Rock, à cause d'une trop forte activité du 53Mn. Dans ce cas, INCL permet de conclure qu’il faut se poser la question d'un problème avec la mesure de l'échantillon.
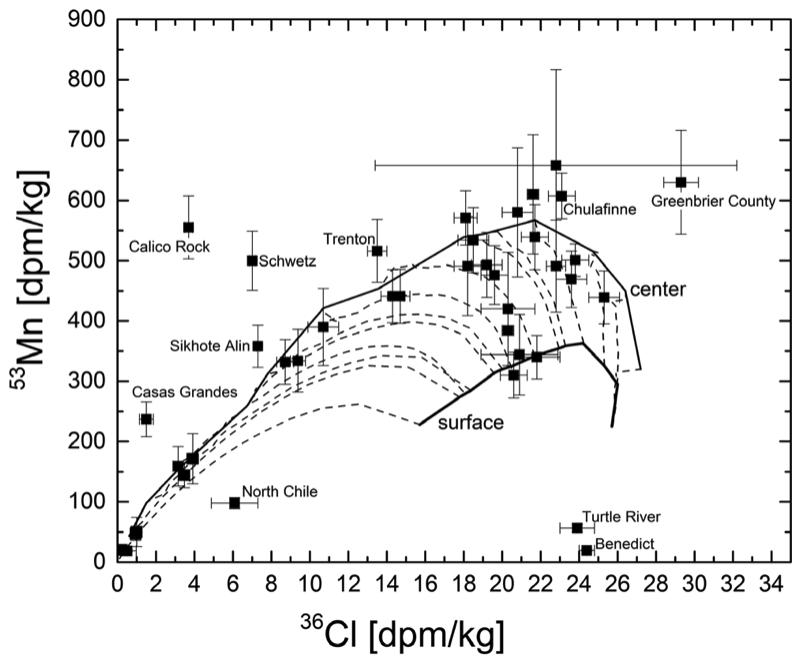
Figure 2 : Taux de production du 53Mn en fonction du taux de production du 36Cl dans des météorites ferreuses. Les lignes pointillées donnent les résultats de calcul à l'intérieur d'une météorite de rayon pré-atmosphérique allant de 5 cm à 120 cm, ainsi que les 2 m en surface d'un objet de 10 m. Les lignes noires relient les résultats pour toutes les surfaces et tous les centres, respectivement. Les prédictions du modèle définissent une zone de combinaisons de taux de production autorisées de 36Cl-53Mn. Des données expérimentales sont également présentées. Les météorites se trouvant en dehors de la zone autorisée sont nommées.
Conclusion
Les mécanismes de production et les durées de vie des isotopes 53Mn et 60Fe sont des observables précieux pour décrypter l'histoire des météorites ferreuses. Les progrès faits dans les techniques de préparation des échantillons et les mesures de spectrométrie de masse, d'une part, et, d'autre part, dans la modélisation des réactions nucléaires par le code INCL, associé au code Abla, ont permis d'utiliser ces deux isotopes dans une études récentes [1]. Les comparaisons calcul/mesure ont permis de montrer la fiabilité de la modélisation, d’étudier certaines caractéristiques comme les tailles des météorites de Grant (40cm) et de Twannberg (jusqu’à 10m). Elle permettent aussi de progresser sur l'histoire de certaines météorites, en suggérant des scénarii de collisions, et enfin de faire des analyses critiques sur les méthodes mises en jeu dans l'étude, pointant notamment des échantillons suspects. À l’avenir, les améliorations envisagées d’INCL devraient permettre de mieux reconstruire les histoires individuelles des météorites, au-delà des seules météorites ferreuses.
Références
[1] I. Leya et al., Meteoritics & Planetary Science 1–14 (2020).
[2] J.-C. David and I. Leya, Progress in Particle and Nuclear Physics 109 (2019) 103711
[3] Berger E. L. et al., Meteoritics & Planetary Science 42:A18 (2007).
[4] Smith T. et al., Meteoritics & Planetary Science 52:2241–2257 (2017); Smith T. et al., Meteoritics & Planetary Science 54:2951–2976 (2019).
Contact
• Structure de la matière nucléaire › Dynamique des réactions nucléaires
• Le Département de Physique Nucléaire (DPhN)
• Laboratoire d'études et d'applications des réactions nucléaires (LEARN)



