Un programme scientifique important est consacré à la structure tridimensionnelle du proton en termes de ces constituants élémentaires, quarks et gluons. Une nouvelle génération d’installations expérimentales, à Jefferson Lab (US), au CERN, et peut-être plus tard auprès d’un futur collisionneur électrons-ions (EIC), devrait permettre de réaliser une tomographie du proton avec une précision inégalée. Le succès de ce programme passe par l’extraction de quantités appelées distributions de partons généralisées (GPD) à partir d’une grande variété d’observables. L’Irfu, en partenariat avec des instituts américain, espagnol et italiens, a franchi une étape décisive en construisant de manière systématique des modèles de GPD obéissant à priori à toutes les contraintes théoriques requises. Ces résultats font l’objet de deux publications dans les revues à fort impact Eur. Phys. J. C. [1] et Phys. Lett. B [2].
Que pouvons-nous faire de mieux que Rutherford au siècle dernier ?! Cette question fit l’objet d’une table ronde sur la structure du nucléon dans une conférence internationale récente [3]. Elle permit d’illustrer la richesse des développements théoriques et expérimentaux des 20 dernières années, et de souligner les promesses des nouvelles générations d’expériences. En particulier, le concept de distribution de partons généralisée (GPD) propose de cartographier les propriétés du proton (probabilité de présence des quarks et gluons, distribution de charge électrique, etc.). Ces GPD sont d’ores et déjà accessibles expérimentalement, notamment lorsque le proton est sondé via le canal de diffusion Compton profondément virtuelle (DVCS). Ce canal, dans lequel un électron (ou un muon) interagit avec un proton pour produire un électron (ou un muon), un photon et un proton dans l’état final [4], est étudié par les équipes de l’Irfu à Jefferson Lab et au CERN.
D’un point de vue phénoménologique, la difficulté de cette tâche réside dans le fait que les GPD ne sont pas directement les quantités mesurées. Le lien entre les observables et les GPD est complexe mais sous bon contrôle théorique. Il s’agit donc d’un problème inverse, que les physiciens résolvent en général en choisissant une forme fonctionnelle de la GPD à extraire des données, forme fonctionnelle qui dépend d’un certain nombre de paramètres dont les valeurs sont alors ajustées de manière à reproduire au mieux les signaux expérimentaux. Cependant, les GPD ont ceci de spécifique qu’elles doivent obéir à un grand nombre de contraintes issues de principes physiques premiers. Ces contraintes sont suffisamment fortes pour exclure les paramétrisations naïves, mais trop faibles pour aboutir à une description unique des GPD. Depuis 2002, les physiciens ont tenté des extractions, soit en négligeant une partie des contraintes théoriques requises, soit en s’appuyant sur des formes fonctionnelles trop rigides pour s’accommoder des données expérimentales. Cela induisait des effets systématiques qui étaient acceptables au regard de la précision des premières mesures DVCS, mais qui seront intenables dans l’ère de précision qui est en train de s’ouvrir.
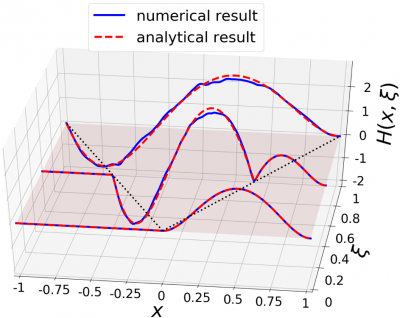
Fig. 1: La GPD H(x, ξ) où x et ξ désignent des fractions de quantité de mouvement du pion portées par le quark dit « actif », i.e. celui qui interagit avec l’électron ou le muon incident du processus DVCS. La courbe rouge correspond à un modèle parfaitement connu, et la courbe bleue à un calcul numérique implémentant les contraintes théoriques sur les GPD à partir de la connaissance du modèle initial sur le domaine x > ξ. L’accord entre le modèle test et sa reconstruction à partir de données parcellaires est excellent.
Au prix d’un effort de modélisation débuté fin 2014, et d’une approche originale, il a été possible de résoudre ce problème ouvert depuis une quinzaine d’années. La solution passe par l’inversion d’une transformation mathématique bien connue en tomographie médicale, la transformation de Radon. En tomographie par transmission, une section d’un corps humain est scannée par un étroit faisceau de rayons X dont la perte d’intensité est enregistrée par un détecteur. La transformation de Radon décrit mathématiquement cette perte d’intensité le long de la direction de propagation du faisceau, et l’inversion de la transformation de Radon livre les images à deux dimensions qui sont utilisées par les médecins pour établir leur diagnostic. Comment faire le lien avec notre problème de modélisation des GPD ? Le principe de la solution consiste à construire une GPD de manière flexible, avec des paramètres qui seront plus tard ajustés aux données expérimentales, sur un sous-ensemble de son domaine de définition. En inversant la transformation de Radon, il est possible d’étendre cette forme fonctionnelle à l’intégralité du domaine de définition en garantissant la conformité aux principes physiques premiers. La solution du problème de modélisation des GPD mêle donc des considérations de physique nucléaire, d’analyse fonctionnelle et de calcul scientifique. L’algorithme obtenu permet la construction systématique de formes fonctionnelles satisfaisant a priori toutes les bonnes propriétés théoriques, indépendamment de la valeur des paramètres libres à ajuster aux données expérimentales. Cet algorithme a été testé avec succès sur plusieurs cas représentatifs. Il s’agissait de vérifier qu’il était possible, avec un algorithme unique, de reproduire les quelques cas particuliers connus de modèles de GPD tout en respectant les principes physiques premiers pour chacune d’elles (Fig. 1).
Cette avancée théorique ouvre de nouvelles portes, et ne se limite pas à la structure du nucléon. Une application immédiate de cette nouvelle approche au cas du pion (le plus léger des états constitués d’un quark et d’un antiquark) a permis une amélioration significative d’un modèle ab initio développé en 2015 et qui avait fait l’objet du fait marquant « Rétroconception des hadrons ».
Références
[1] N. Chouika et al., Eur. Phys. J. C77 (2017) 906.
[2] N. Chouika et al., Phys. Lett. B780 (2018) 287.
[3] N. Stefanis et al., EPJ Web Conf. 137 (2017) 01003.
[4] K. Kumeri?ki et al., Eur. Phys. J. A52 (2016) 157.
Contacts
• Structure de la matière nucléaire › Structure en quarks et gluons des hadrons
• Institut de recherche sur les lois fondamentales de l'Univers (Irfu) • Le Département de Physique Nucléaire (DPhN)
