Une nouvelle méthode permettant l’étude de la déformation des noyaux atomiques vient d’être mise au point en se basant sur le fait, récemment mis en lumière, que les expériences de collision nucléaire réalisées dans les collisionneurs à haute énergie, tels que le collisionneur d'ions lourds relativistes (RHIC) du BNL ou le grand collisionneur de hadrons (LHC) du CERN, sont sensibles à la forme des isotopes mis en jeu dans les dites collisions. Ainsi, une collaboration entre théoriciens des hautes et basses énergies, dont des chercheurs de l'Irfu, a démontré qu'il est possible d'obtenir des informations quantitatives sur les déformations nucléaires et a montré que l'isotope 129Xe présente une forme triaxiale, c'est-à-dire un sphéroïde à trois axes inégaux. Ce résultat représente la première preuve de triaxialité pour un état fondamental nucléaire obtenue dans des expériences à haute énergie. En outre, il ouvre la voie à de futures recherches passionnantes à l'interface de la physique nucléaire de basse et haute énergies.
L'interprétation du comportement collectif des noyaux atomiques en termes de formes déformées est au cœur de notre compréhension des divers phénomènes émergents qu’ils exhibent et qui se manifestent dans des conditions et des échelles d’énergies très différentes, allant de l’énergie nucléaire jusqu’aux processus astrophysiques. Expérimentalement, la déformation nucléaire est traditionnellement étudiée en réalisant des expériences de basse énergie. Récemment, cependant, une collaboration de physicien s'est rendue compte que l'on pouvait accéder à la forme des noyaux également dans des expériences de collision d'ions à haute énergie.
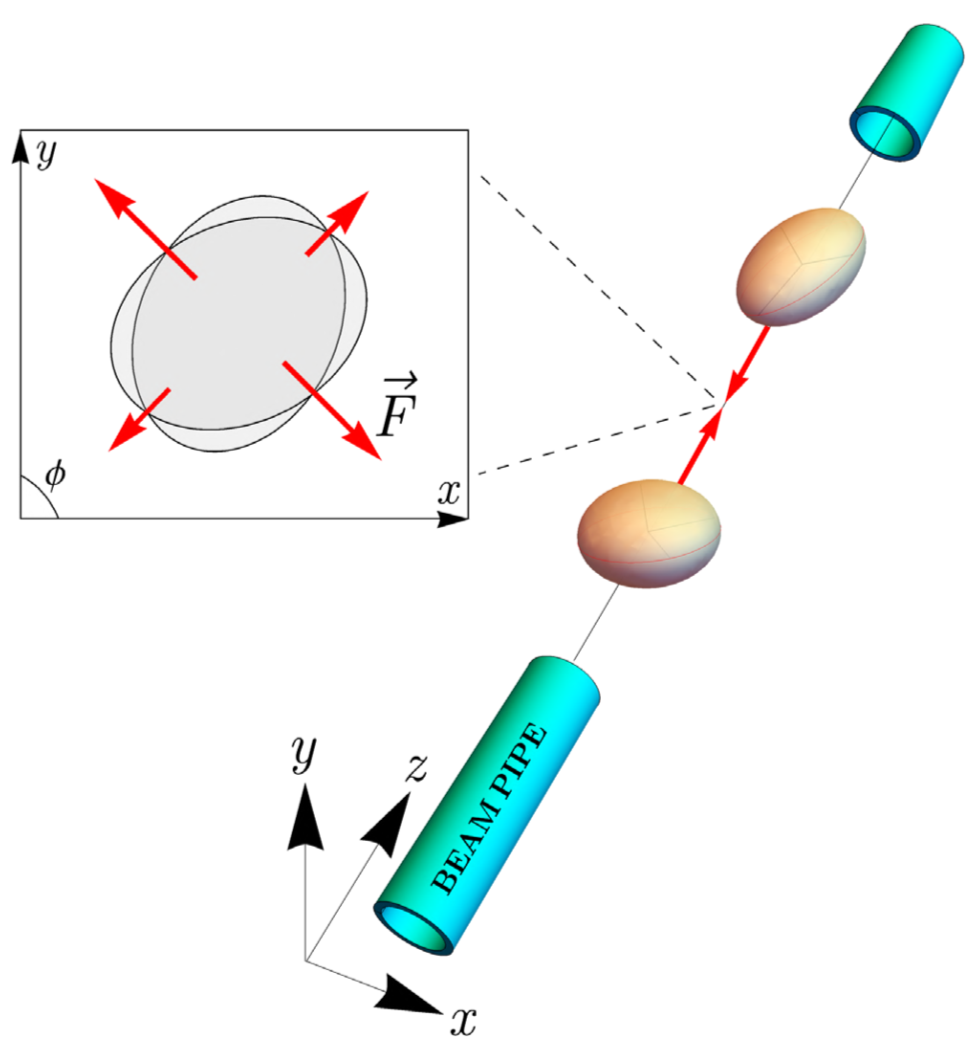
Figure 1. Illustration d'une collision frontale entre deux noyaux atomiques réalisée dans un collisionneur d’ions lourds. Les noyaux, déformés dans leur état fondamental, sont orientés aléatoirement lors de leur passage dans le tube du faisceau et la forme de leur zone de recouvrement peut aller de circulaire à elliptique. L'expansion du milieu créé dans le plan perpendiculaire au faisceau (x,y) est pilotée par un champ de force F qui présente la même anisotropie que la zone de recouvrement. Notez que dans le référentiel du laboratoire, les deux noyaux ressembleraient à de fines crêpes, comprimées dans la direction z du faisceau, en raison d'une forte contraction de Lorentz.
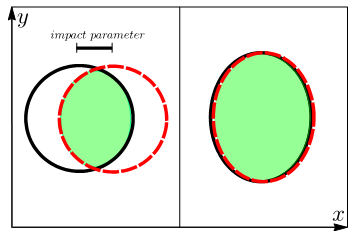
Figure 2. Régions de chevauchement anisotropes dans les collisions nucléaires. À gauche : une collision de noyaux sphériques rompt l'anisotropie dans le plan transversal en raison du paramètre d'impact fini. À droite : une collision centrale de noyaux déformés rompt l'anisotropie en raison de la forme non sphérique des corps en collision.
En effet, dans de telles collisions, la géométrie joue un rôle crucial. Comme le montre la Fig. 1, lors de la collision de deux noyaux déformés, la géométrie de la zone de chevauchement sera contrainte par la géométrie des deux noyaux. Si cette zone n'est pas un disque mais une ellipse, elle entrainera une déformation de la distribution des hadrons dans le plan perpendiculaire au faisceau, qui sera détectée dans l'état final de la collision. Cette déformation de la distribution des hadrons est appelée flux elliptique et peut être, in fine, reliée à l'asymétrie initiale de la zone d'interaction. La déformation nucléaire n’est cependant pas toujours la seule source du flux elliptique. Comme l'illustre la figure 2, dans le cas de noyaux sphériques, mais de collisions non centrales (côté gauche), la région d'interaction est déformée et génère un flux elliptique. Par conséquent, la sélection des événements les plus centraux est cruciale pour étudier la forme des noyaux.
Peut-on traduire ces considérations géométriques en estimations quantitatives ? Il s'avère que les collisions d'isobares (c'est-à-dire de nucléides ayant un nombre différent de protons mais le même nombre de nucléons) permettent de le faire très proprement. En effet, si les deux nucléides sont caractérisés par la même forme et le même nombre de nucléons, le même flux elliptique sera produit lors des collisions, et le rapport des flux elliptiques sera égal à un. Au contraire, tout écart significatif par rapport à l'unité indique des déformations initiales différentes des deux noyaux. En particulier, la collaboration a démontré qu'une telle déviation peut être reliée à des paramètres de forme spécifiques des deux isobares [1]. Les simulations de Monte Carlo ont ensuite confirmé que l'effet est important et ont fourni des prédictions pour deux ensembles de collisions isobares, à savoir 96Ru vs 96Zr et 154Sm vs 154Gd (voir la figure 3, où les rapports dépassent en effet significativement l'unité vers la centralité zéro, c'est-à-dire pour les collisions frontales). Récemment, la collaboration STAR (l'un des détecteurs RHIC à Brookhaven, USA) a publié des données expérimentales sur le premier cas qui confirment cette prédiction.
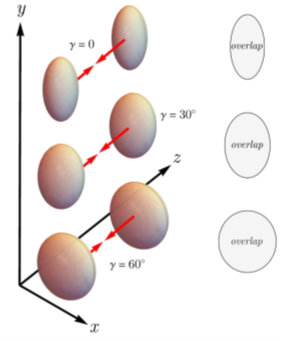
Figure 4. Les collisions frontales à petites valeurs de la quantité de mouvement transversal moyenne des hadrons détectés permettent d'isoler les configurations qui maximisent la zone de recouvrement. En fonction de la valeur de l'angle contrôlant le déséquilibre de longueur des axes du sphéroïde déformé (étiqueté ?), les configurations de collision à faible quantité de mouvement transversal moyenne des hadrons peuvent ainsi varier entre des géométries brisant au maximum la symétrie azimutale (?=0°) et des géométries symétriques azimutales (?=60°).
Peu après, une autre percée a été réalisée, basée sur le fait que la quantité de mouvement moyenne des hadrons produits (à nouveau dans le plan perpendiculaire au faisceau) peut être utilisée pour évaluer l'orientation relative des deux noyaux au point de collision. Pour les collisions d'un isotope (déformé) donné, cela peut être exploité pour sélectionner les événements dans lesquels la zone de chevauchement est maximale. Il est important de noter que la forme de cette zone de recouvrement sera différente selon que le noyau a une déformation prolate, oblate ou triaxiale (cette dernière désignant un sphéroïde à trois axes inégaux, voir la figure 4).
En conséquence, l'écoulement elliptique observé nous permet de distinguer ces possibilités, c'est-à-dire de déterminer le paramètre γ contrôlant le déséquilibre en longueur des axes du sphéroïde déformé. Ce paramètre varie de 0° (forme prolate ou oblong) à 60° (forme oblate). Les théoriciens de l'Irfu, de Madrid, de Lyon et de Heidelberg ont vérifié ces résultats en effectuant des calculs de structure nucléaire de pointe du noyau 129Xe, puis des simulations de Monte Carlo pour les collisions relativistes de ces isotopes [2]. Les résultats sont présentés à la figure 5 et une différence nette dans l'observable considéré (ici le corrélateur de Pearson) peut être observée entre les noyaux oblates (courbe bleue en pointillés) et les noyaux allongés (courbe verte en pointillés). Les configurations triaxiales se situent entre les deux (courbe rouge pointillée), tandis que les courbes noires pleines correspondent au résultat obtenu pour un noyau sphérique, 208Pb.
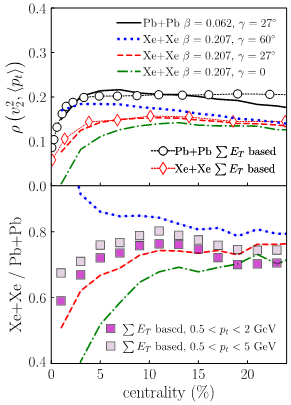
Figure 5. Résultats théoriques et expérimentaux concernant la corrélation entre le flux elliptique et la quantité de mouvement transversal moyenne. Les symboles représentent les mesures préliminaires de la collaboration ATLAS (CERN). En haut : l’évolution du coefficient du corrélation de Pearson en fonction de la centralité des collisions 208Pb-208Pb et 129Xe-129Xe. En bas : leur rapport.
La comparaison des résultats théoriques avec les données préliminaires de la collaboration ATLAS au CERN [3] indique que le 129Xe a une forme triaxiale (voir Fig. 5), avec des paramètres de déformation compatibles avec ceux du 130Xe voisin, récemment déterminés dans une expérience à basse énergie [4]. Ce résultat représente la première preuve de la triaxialité pour un état fondamental nucléaire obtenue dans des expériences à haute énergie. En outre, il ouvre la voie à de futures recherches passionnantes à l'interface de la physique nucléaire de basse et haute énergies.
References
[1] G. Giacalone, J. Jia, V. Somà, Phys. Rev. C 104 L041903 (2021)
[2] B. Bally, M. Bender, G. Giacalone, V. Somà, Phys. Rev. Lett. 128 082301 (2022)
[3] The ATLAS collaboration, arXiv:2205.00039 (2022)
[4] L. Morrison et al., Phys. Rev. C 102 054304 (2020)
Contacts
• Structure de la matière nucléaire › Structure en quarks et gluons des hadrons
• Institut de recherche sur les lois fondamentales de l'Univers (Irfu) • Le Département de Physique Nucléaire (DPhN)
