Predicting properties of, e.g., molecules or atomic nuclei from first principles requires to solve the Schrödinger equation with high accuracy. The computing cost to find exact solutions of the Schrödinger equation scales exponentially with the number of particles constituting the system. Thus, with nuclei composed of tens or hundreds of nucleons, it necessitates accurate approximate methods of lower computing cost. However, such methods can be applied to a limited number of systems: the weakly correlated ones. Consequently, a universally applicable method is still missing. Employing a novel formalism recently developed at Irfu/DPhN [1], highly accurate solutions of the Schrödinger equation – in the context of the exactly solvable Richardson model - have been obtained, independently of the weakly- to strongly-correlated character of the system. This work has been performed in collaboration with ab initio quantum chemists from Rice University. This exciting new achievement, paving the way for precise ab initio computations of molecular or nuclear properties of a large number of systems, was recently published in Physical Review C [2] and highlighted as the Editor’s suggestion.
Molecules and atomic nuclei are finite mesoscopic quantum systems, i.e. they are neither microscopic systems made out of a few particles nor macroscopic systems made out of a very large number of them, which makes their description particularly arduous. While the degrees of freedom at play in the former are A electrons interacting via the Coulomb force, the latter are effectively modelled in terms of A strongly interacting neutrons and protons. While properties of these systems strongly depend on the nature of their constituents and interactions, the physics of the system is governed by the same dynamical equation, i.e. the A-body Schrodinger equation. As a result, the difficulty to make accurate predictions is mostly independent of the nature of the particles and of their interactions.
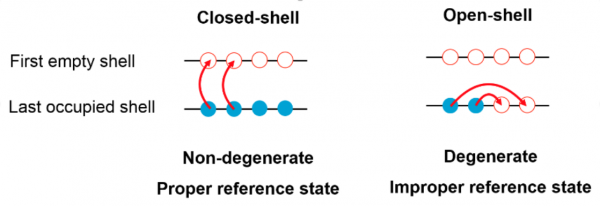
Figure 1: Schematic representation of the last occupied and first empty shell in the reference state obtained via a zeroth-order description of the system. Arrows embody the processes by which correlations are captured beyond that zeroth-order description.
The fact that a molecule or an atomic nucleus displays weak or strong correlations is empirically related to the picture at play in the zeroth-order description of the system. In this description, the A particles are placed on the A lowest quantum levels whose degree of degeneracy, i.e. the number of fermions (electrons or nucleons) that can sit on a given level or “shell”, is related to the symmetries displayed by the physical system. If A is such that all levels including (but) the highest one are fully occupied, the system is said to be of “closed-shell” (“open-shell”) character and typically displays weak (strong) correlations. These two situations are schematically illustrated in Fig. 1.
As a result of the two-fold degeneracy of electronic shells, most molecules are closed-shell in their ground state but do transition through an open-shell-like state when breaking chemical bonds. Contrarily, rotational symmetry induces a larger degree of degeneracy for nuclear shells, making the large majority of nuclear ground states to be of open-shell character. Furthermore, only the nuclei exhibiting both neutron and proton closed shells, i.e. so-called doubly-magic nuclei, are weakly correlated. The dominance of open-shell nuclei is illustrated in Fig. 2. One key manifestation of strong correlations in open-shell nuclei relates to their superfluid character.
Solving the A-body Schrodinger equation, whose naïve cost grows exponentially with A, constitutes a highly non-trivial problem from the formal and computational perspectives. So-called “brute force” methods attacking directly this cost are thus limited to systems with A ≤ 15. To describe heavier systems, one must resort to approximate methods whose cost is polynomial with A.
Whenever a system is of closed-shell character, polynomially-scaling methods can be designed by expanding the exact solution of the A-body Schrodinger equation around a Slater determinant, i.e. the zeroth-order reference state discussed above. Indeed, the fact that the reference state is not degenerate with respect to elementary fermion excitations denoted by red arrows in Fig. 1, i.e. the promotion of nucleons from occupied to unoccupied shells in the reference state, makes it possible to capture weak correlations in a controlled and meaningful way. All polynomially-scaling methods are based on this principle.
Over the years, several polynomially-scaling methods delivering highly accurate results for weakly-correlated systems have been designed and applied. One typical example constituting the golden standard in ab initio quantum chemistry and that is now flourishing in nuclear physics, is the so-called coupled cluster (CC) formalism. However, these methods typically fail in the presence of strong correlations such that research activities currently focus on the design of novel formalisms that can be universally applied to A-body systems with 2 ≤ A ≤ few hundreds, independently of the fact that they are weakly or strongly correlated.
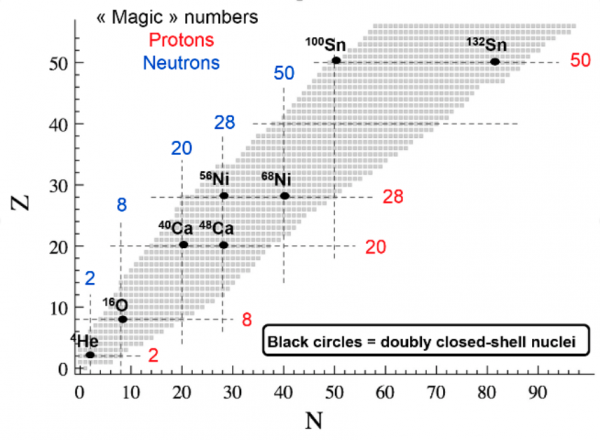
Figure 2: Low portion of the Segrè chart representing known and predicted-to-exist atomic nuclei below the Barium element (Z=56). N (Z) denotes the neutron (proton) number of a given nucleus. Vertical (horizontal) dashed lines locate the neutron (proton) closed shells (“magic numbers”). Bullets at the crossing of these lines embody doubly closed-shell (doubly “magic”) nuclei that are typically weakly correlated. The remaining nuclei are of singly or doubly open-shell character and are thus typically strongly correlated.
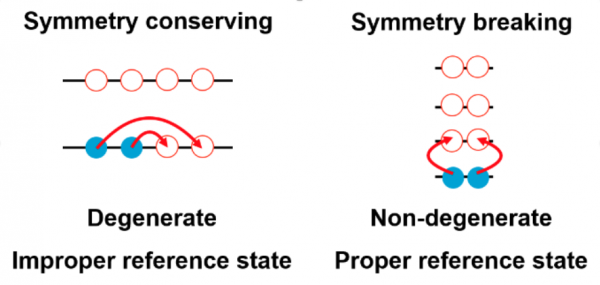
Figure 3: Schematic shell sequence and shell filling for an open-shell nucleus in a symmetry-conserving (left) and a symmetry-breaking (right) zeroth-order description.
Whenever the system is open-shell, the possibility to promote fermions from occupied to unoccupied levels at no energy cost (see Fig. 1) makes the methods ill-defined and incapable of capturing the associated strong correlations. A powerful way to bypass this impediment while maintaining the polynomial cost of the method is to authorize one or several symmetries of the system to spontaneously break in the zeroth-order description. Doing so lifts the degeneracy of elementary excitations such that the system effectively acquires a closed-shell character as schematically illustrated in Fig. 3. Starting from the newly obtained reference state, the solution of the Schrodinger equation can be safely expanded and strong correlations captured both via the new reference state and the expansion around it.
The case of present interest consists of authorizing the so-called U(1) global gauge symmetry, an abstract symmetry associated with the fact that nuclei contain specific numbers of protons and neutrons, to break in order to capture the superfluid character of open-shell nuclei via the use of a so-called Bogoliubov reference state. That this reference state breaks U(1) symmetry means that it does not contains a sharp number of neutrons and/or protons but rather mixes several neighboring values.
In the past years, theoreticians from Irfu/DPhN have developed three different expansion methods allowing U(1) symmetry to break, thus producing the first systematic ab initio calculations of mid-mass singly open-shell nuclei [3]. One of these three methods, coined as Bogoliubov CC (BCC) theory [4], generalizes standard CC theory applicable to closed-shell systems. While the exact solution necessarily displays a well-defined number of nucleons, approximate solutions obtained through these expansion methods do not as mentioned above. Though such a breaking can be real in macroscopic systems, it is only fictitious in finite quantum systems such that obtaining an accurate solution eventually requires restoring the broken symmetry, i.e. the specific number of nucleons in the present case. This task, a long-term challenge in many-body theory, was recently achieved by theoreticians from Irfu/DPhN via the formulation of the so-called particle-number-projected Bogoliubov CC (PBCC) theory [1]. In this formalism, U(1) symmetry is broken to authorize a meaningful expansion and further restored to obtain a correct symmetry solution that fully captured strong, i.e. superfluid, correlations.
The best way to first gauge the performance of a novel many-body method is to use it to describe a model problem whose exact solutions are known. This was achieved for PBCC in collaboration with quantum chemists from Rice university [2] on the basis of the well-celebrated Bardeen-Cooper-Schrieffer (BCS) pairing problem whose exact solutions were provided long ago by Richardson [5]. This solvable problem is perfectly suited given that its solutions transition, when tuning the interaction strength between the particles in the model, from a normal (weakly correlated) to a superfluid (strongly correlated) state. As illustrated in Fig. 4, the newly designed PBCC method (coined as Projected BCS-CC on the figure) delivers essentially exact ground-state energies for all interaction strengths, improving decisively over the unprojected BCC method (coined as BCS-CC) as well as over the unprojected or projected zeroth-order descriptions (respectively coined as BCS and Projected BCS). PBCC provides these results while retaining a polynomial cost not too much larger than the unprojected BCC method.
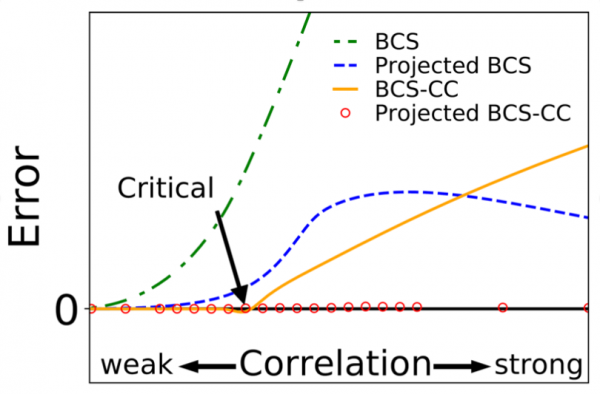
Figure 4: Ground-state energy errors (arbitrary units) against the exact solution of the Richardson many-body problem as a function of the interaction strength. The critical point denotes the phase transition between the normal and the superfluid phases. Polynomial methods that do no break U(1) symmetry (results not reproduced here) cannot deliver any sensible results in the superfluid phase. The combined benefit of (i) breaking the symmetry before (ii) capturing correlations beyond the zeroth order description while (iii) restoring the symmetry is clearly illustrated.
In summary, the theoreticians from Irfu/DPhN have designed and tested a novel many-body formalism delivering highly accurate solutions of the exactly solvable Richardson many-body problem in all situations ranging from weak to strong correlations. The next step consists in implementing the many-body method to compute ab initio properties of molecules and atomic nuclei independently of their weakly or strongly correlated character.
[1] T. Duguet, A. Signoracci, J. Phys. G: Nucl. Part. Phys. 44 (2016) 015103
[2] Y. Qiu, T. M. Henderson, T. Duguet, G. E. Scuseria, Phys. Rev. C99 (2019) 044301
[3] V. Somà, C. Barbieri, T. Duguet, Phys. Rev. C87 (2013) 011303(R)
[4] A. Signoracci, T. Duguet, G. Hagen, G. R. Jansen, Phys. Rev. C91 (2015) 064320
[5] R. W. Richardson, Phys. Lett. 3 (1963) 277 ; Phys. Rev. 141 (1966) 949
• Structure of nuclear matter › Atomic nucleus
• Institute of Research into the Fundamental Laws of the Universe • The Nuclear Physics Division
