Dans sa version la plus courante, l’imagerie muonique est une technique intrinsèquement 2D : en effet les densités mesurées sont intégrées le long de la direction d’observation de l’instrument. En principe, une cartographie 3D peut tout de même être obtenue en combinant plusieurs projections, comme en imagerie médicale. Mais dans le cas de la muographie, le nombre de projections disponibles est généralement très réduit, à cause du temps d’acquisition nécessaire à chaque image. Un algorithme d’imagerie 3D vient d’être utilisé avec succès sur le télescope à muons TomoMu, dans le cadre d’une collaboration entre l’Université de Florence et l’Irfu. La structure 3D d’un objet test a été reconstruite avec seulement 3 prises de vue, grâce notamment à l’excellente résolution de l’instrument. Cette avancée très importante permet maintenant d’envisager l’étude de structures plus complexes, avec des applications variées depuis l’étude de réacteurs nucléaires en phase de démantèlement jusqu’à l’exploration des sols.
Introduction
L’imagerie muonique est une technique non destructive et très pénétrante qui utilise les muons issus du rayonnement cosmique pour sonder l’intérieur des objets (figure ci-contre). Depuis sa toute première utilisation en 1955, cette technique a bénéficié de nombreux progrès à la fois instrumentaux (détecteurs de particules) et logiciels (algorithmes de reconstruction). En 2003, une équipe de Los Alamos a mis au point la première imagerie muonique en 3D en utilisant la diffusion des muons dans la matière, en entourant des objets de taille nécessairement modeste avec des détecteurs de particules. En 2015, la structure 3D d’un volcan a été esquissée avec des instruments de résolution limitée. En 2017, un vide inconnu a été détecté depuis la Galerie Bourbon à Naples, et localisé précisément avec des mesures complémentaires. La même année, l’utilisation de détecteurs ultra-précis a permis de révéler et localiser une cavité au cœur de la grande pyramide de Khéops. Les télescopes à haute définition de l’Irfu ont permis à cette occasion la toute première détection de structures internes d’une pyramide depuis l’extérieur. Il est alors clairement apparu qu’une tomographie 3D de précision était à portée de muon pour n’importe quelle taille d’objets, en combinant des projections 2D haute définition avec un algorithme 3D robuste et dédiée aux faibles nombres de projections.
Une muographie 2D d’une structure 3D (la pyramide de Khéops).
(Gauche): la première couche de Plomb de l’objet cible. (Droite): deux des trois mesures de la cible dans TomoMu.
Dispositif expérimental
Nous avons décidé d’utiliser ici la muographie par absorption comme technique d’imagerie 2D. La muographie par absorption diffère légèrement de la muographie par transmission employée pour les grandes structures, mais toutes les deux mesurent l’opacité X, c’est-à-dire la densité intégrée le long d’une direction :
X(θ,φ)=∫ρdL
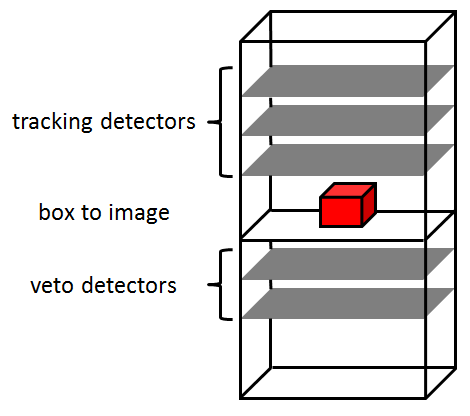
La cible à imager était composée de briques de Plomb agencées dans une boîte de 15 cm de côté (voir figure ci-contre). Les mesures ont été effectuées avec le télescope TomoMu avec trois orientations différentes de la cible. Pour ces mesures, TomoMu comprenait cinq détecteurs Micromegas, trois en partie haute pour reconstruire la trajectoire des muons et deux en partie basse agissant comme un véto pour identifier les muons absorbés (voir figure ci-dessous).
Reconstruction 3D (problème inverse)
De manière générale, on effectue une tomographie en divisant le volume à imager en une matrice de pixels 3D appelés voxels. Pour cette étude, les voxels étaient cubiques et de 1 à 3 cm de côté, pour un nombre total J compris entre 1000 et 6000. L’information sur l’opacité fournie par la probabilité d’absorption des muons est rassemblée dans des objets appelés rayons qui peuvent être définis géométriquement comme des directions discrètes (spatialement et en angle). Pour cette analyse, le nombre de rayons, I, était de l’ordre de 3000.
Chaque rayon doit être calibré pour convertir la probabilité d’absorption en mesure de l’opacité. Trois mesures de calibration ont ainsi été effectuées avec des couches uniformes de Plomb (0 cm, 5 cm et 10 cm). La reconstruction de la distribution 3D de la densité de l’objet requiert alors la résolution du système d’équations suivant :
Xi=Σj Lijρj
où :
Algorithmes ART and SART
La technique de reconstruction algébrique (Algebraic Reconstruction Technique, ART) est un algorithme itératif qui permet de résoudre un système d’équations linéaires dans le cas où les nombres d’équations et d’inconnus sont grands. Le vecteur des J inconnus (ici la densité dans chaque voxel) peut être représenté comme un point dans un espace à J dimensions tandis que les I équations (correspondant chacune à une mesure d’opacité) forment I hyperplans dans ce même espace. L’algorithme ART permet de résoudre ce problème en projetant séquentiellement et de manière itérative le vecteur des densités sur chaque hyperplan. Dans l’algorithme ART simultané (Simultaneous ART, ou SART), une seule itération combine toutes les projections d’un coup en les moyennant. En plus d’offrir une convergence plus rapide, la version SART permet de facilement prendre en compte les erreurs statistiques associées à chaque mesure en pondérant les projections sur chaque hyperplan.
Résultats et développements futurs
Après 10 itérations de l’algorithme SART (ce qui ne prend que 0,4 seconde!), un bon accord a été obtenu entre la densité 3D reconstruite et la densité réelle de l’objet. En particulier son contour est bien reproduit, et les valeurs de densité sont compatibles avec la densité des briques de Plomb (figure ci-contre).
Des études additionnelles sont maintenant prévues afin de mieux définir et comprendre le critère d’arrêt de l’algorithme itératif, et en particulier la stabilité des résultats en fonction de la taille relative des voxels et des rayons. Cette méthode sera également bientôt testée avec des objets de plus grande taille, comme des mines, des réacteurs nucléaires ou des pyramides. Dans certains cas, l’implémentation d’un algorithme ART discret (Discrete ART ou DART) pourra servir à mieux contraindre le problème en limitant les valeurs de densité à un ensemble discret (par exemple celle de l’air et de la roche).
Pour aller plus loin:
ART & SART : A. C. Kak, M. Slaney and G. Wang, "Principles of computerized tomographic imaging." Medical Physics 29.1 (2002): 107-107. Chapter 7
DART : K. J. Batenburg and J. Sijbers, "DART: a practical reconstruction algorithm for discrete tomography", IEEE Transactions on Image Processing (2011), 20.9: 2542-2553.
Contacts:
G. Baccani (Etudiant en thèse de l’Université de Florence, et principal auteur de ce travail lors d’un séjour de 3 mois à Saclay, )
S. Procureur (CEA/Irfu)
Distribution de densité dans les plans médians (horizontaux) des deux couches de Plomb composant l’objet cible. La ligne noire indique le contour réel des briques en Plomb. Les valeurs de densité (échelle de couleur) sont normalisées à celle du Plomb.
• Détection des rayonnements › Réalisations en réponse aux enjeux sociétaux › MPGD Activities Constituants élémentaires et symétries fondamentales
• Institut de recherche sur les lois fondamentales de l'Univers (Irfu) • Le Département d'Électronique des Détecteurs et d'Informatique pour la Physique (DEDIP) • Le Département de Physique des Particules (DPhP) • Le Département de Physique Nucléaire (DPhN)
PHoCEA DRF 2024 - Tous droits réservés - Mentions légales - Ce site utilise Bootstrap
Dernière mise à jour : 21-11-2024
