Prédire, par exemple, les propriétés des molécules ou des noyaux atomiques à partir des principes de base nécessite de résoudre l'équation de Schrödinger avec une grande précision. Le coût de calcul pour trouver des solutions exactes de l'équation de Schrödinger augmente de manière exponentielle avec le nombre de particules constituant le système. Ainsi, pour des noyaux composés de dizaines ou de centaines de nucléons, il faut recourir à des méthodes approximatives précises dont le coût de calcul est moindre. Ces méthodes sont aujourd’hui appliquées à un nombre limité de systèmes : ceux qui sont faiblement corrélés. Par conséquent, il manque encore une méthode applicable de manière universelle. En utilisant un nouveau formalisme récemment développé à l’Irfu/DPhN [1], des solutions très précises de l'équation de Schrödinger - dans le cadre du modèle de Richardson qui peut être résolu exactement - ont été obtenues, indépendamment du caractère faiblement à fortement corrélé du système. Ce travail a été réalisé en collaboration avec des chimistes quantiques utilisant des méthodes ab initio de l'Université de Rice. Ce nouveau résultat passionnant, qui ouvre la voie à des calculs ab initio précis des propriétés moléculaires ou nucléaires d'un grand nombre de systèmes, a récemment été publié dans la revue Physical Review C [2] et mis en avant comme Editor’s suggestion.
Les molécules et les noyaux atomiques sont des systèmes quantiques mésoscopiques finis, c'est-à-dire qu'ils ne sont ni des systèmes microscopiques constitués de quelques particules, ni des systèmes macroscopiques constitués d'un très grand nombre d'entre elles, ce qui rend leur description particulièrement ardue. Alors que les degrés de liberté en jeu dans les molécules sont A électrons qui interagissent par la force de Coulomb, les noyaux atomiques sont effectivement modélisés en termes de A neutrons et protons qui interagissent par l’intermédiaire de l’interaction forte. Alors que les propriétés de ces systèmes dépendent fortement de la nature de leurs constituants et de leurs interactions, la physique de ces systèmes est régie par la même équation dynamique, à savoir l'équation de Schrodinger à A corps. Par conséquent, la difficulté de faire des prévisions précises est essentiellement indépendante de la nature des particules et de leurs interactions.
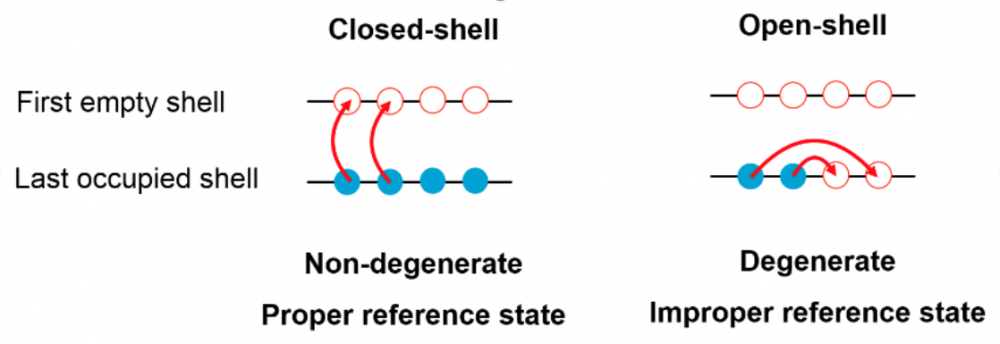
Figure 1 : Représentation schématique de la dernière couche occupée et de la première couche vide dans l'état de référence obtenue par une description à l'ordre zéro du système. Les flèches représentent les processus par lesquels les corrélations sont prises en compte au-delà de cette description d'ordre zéro.
Le fait qu'une molécule ou un noyau atomique présente des corrélations faibles ou fortes est empiriquement lié à l'image que l’on a du système à l’ordre zéro. Dans cette description, les A particules sont placées sur les A niveaux quantiques les plus bas dont le degré de dégénérescence, c'est-à-dire le nombre de fermions (électrons ou nucléons) qui peuvent occuper un niveau donné ou "couche", est lié aux symétries du système physique. Si A est tel que tous les niveaux, y compris (sauf) le plus élevé, sont entièrement occupés, le système est dit "à couche fermée" ("à couche ouverte") et présente généralement de faibles (fortes) corrélations. Ces deux situations sont illustrées de manière schématique en figure 1.
En raison de la double dégénérescence des couches électroniques, la plupart des molécules sont à couche fermée dans leur état fondamental, mais passent dans un état à couche ouverte lorsqu'elles cassent des liaisons chimiques. Au contraire, la symétrie par rotation induit un plus grand degré de dégénérescence pour les couches nucléaires, ce qui fait que la grande majorité des états fondamentaux nucléaires sont à couche ouverte. En outre, seuls les noyaux présentant des couches fermées en neutrons et en protons, c'est-à-dire les noyaux dits doublement magiques, sont faiblement corrélés. La « domination » des noyaux à couche ouverte est illustrée en figure 2. Une manifestation des fortes corrélations dans les noyaux à couche ouverte concerne leur caractère superfluide.
La résolution de l'équation de Schrodinger à A corps, dont naïvement le coût croît de façon exponentielle avec A, constitue un problème non trivial du point de vue formel et informatique. Les méthodes dites "brute force" qui s'attaquent directement à ce coût sont limitées aux systèmes avec A ≤ 15. Pour décrire des systèmes plus lourds, il faut recourir à des méthodes approximatives dont le coût évolue de manière polynomiale avec A.
Lorsqu'un système est à couche fermée, des méthodes polynomiales peuvent être mises en place en développant la solution exacte de l'équation de Schrodinger à A corps autour du déterminant de Slater, c'est-à-dire autour de l'état de référence d'ordre zéro discuté ci-dessus. En effet, le fait que l'état de référence ne soit pas dégénéré par rapport aux excitations de fermions élémentaires indiquées par les flèches rouges de la figure 1, c'est-à-dire la promotion des nucléons de l'état occupé à l'état inoccupé dans l'état de référence, permet de prendre en compte les faibles corrélations de manière contrôlée et significative. Toutes les méthodes polynomiales sont basées sur ce principe.
Au fil des années, plusieurs méthodes polynomiales fournissant des résultats très précis pour des systèmes faiblement corrélés ont été conçues et appliquées. Un exemple typique, constituant « l'étalon-or » de la chimie quantique ab initio et qui est maintenant florissant en physique nucléaire, est le formalisme dit « couple cluster » (CC). Cependant, ces méthodes échouent généralement en présence de fortes corrélations, de sorte que les activités de recherche se concentrent actuellement sur la conception de nouveaux formalismes pouvant être universellement appliqués aux systèmes à A corps, avec 2 ≤ A ≤ quelques centaines, indépendamment du fait qu'ils soient faiblement ou fortement corrélés
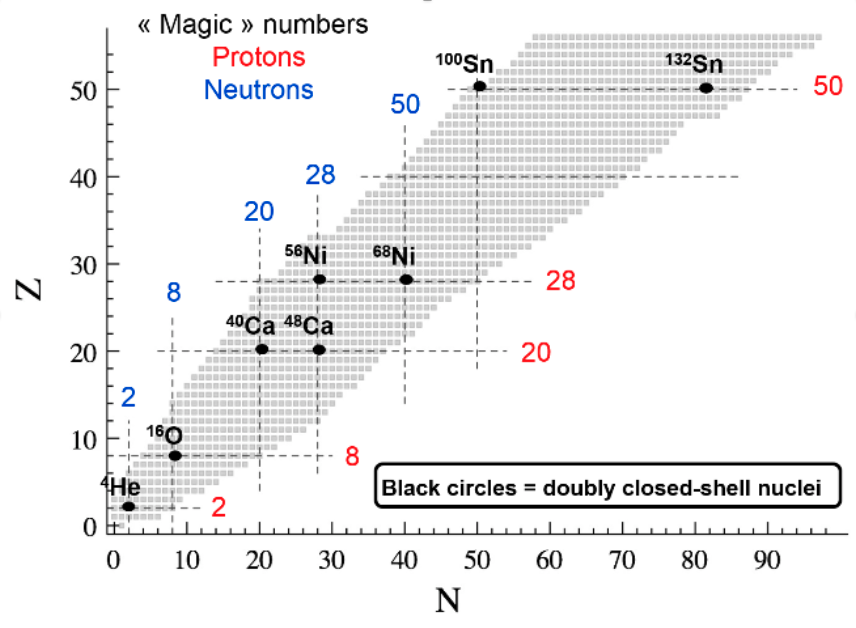
Figure 2 : Partie inférieure de la carte des noyaux représentant les noyaux atomiques connus et prévus sous l'élément Baryum (Z=56). N (Z) désigne le nombre de neutrons (protons) d'un noyau donné. Les lignes verticales (horizontales) en pointillés situent les couches fermées des neutrons (protons) ("nombres magiques"). Les points au croisement de ces lignes représentent les noyaux à couches doublement fermées (doublement "magiques") qui sont généralement faiblement corrélés. Les autres noyaux sont à couche simplement ou doublement ouverte et sont donc généralement fortement corrélés.
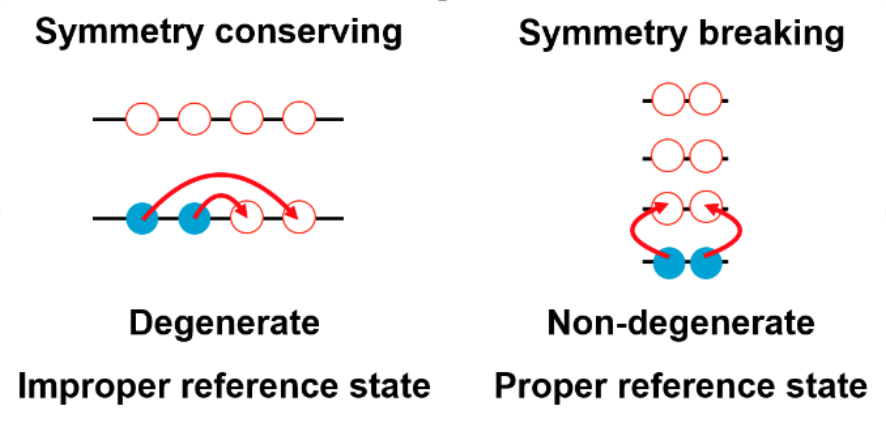
Figure 3 : Schéma d’un noyau à couche ouverte et remplissage de cette couche dans une description d'ordre zéro conservant la symétrie (à gauche) et brisant la symétrie (à droite).
Lorsque le système est à couche ouverte, la possibilité de faire passer les fermions des niveaux occupés aux niveaux inoccupés sans coût énergétique (voir figure 1) rend les méthodes mal définies et incapables de prendre en compte les fortes corrélations associées. Un moyen efficace de contourner cet obstacle, tout en maintenant le coût polynomial de la méthode, consiste à autoriser une ou plusieurs brisures spontanées de symétries du système dans la description à l’ordre zéro. Ce faisant, la dégénérescence des excitations élémentaires est levée, de sorte que le système acquiert effectivement un caractère de couche fermée, comme l'illustre schématiquement la figure 3. À partir de l'état de référence nouvellement obtenu, la solution de l'équation de Schrodinger peut être développée en toute sécurité et les fortes corrélations sont prises en compte à la fois via le nouvel état de référence et le développement autour de celui-ci.
Le cas qui nous intéresse ici consiste à autoriser la symétrie de jauge dite U(1), une symétrie abstraite associée au fait que les noyaux contiennent un nombre spécifique de protons et de neutrons, à se briser afin de capturer le caractère superfluide des noyaux à couche ouverte via l'utilisation d'un état de référence dit de Bogoliubov. Le fait que cet état de référence brise la symétrie U(1) signifie qu'il ne contient pas un nombre fixe de neutrons et/ou de protons, mais qu'il mélange plutôt plusieurs valeurs voisines.
Au cours des dernières années, les théoriciens de l'Irfu/DPhN ont développé trois méthodes d'expansion différentes permettant la brisure de la symétrie U(1), produisant ainsi les premiers calculs ab initio systématiques de noyaux de masse moyenne à couche unique ouverte [3]. L'une de ces trois méthodes, appelée Bogoliubov Couple Cluster (BCC) [4], généralise la théorie du CC standard qui est appliquée aux systèmes à couche fermée. Alors que la solution exacte présente nécessairement un nombre bien défini de nucléons, ce n’est pas le cas des solutions approximatives obtenues par ces méthodes d'expansion comme mentionné ci-dessus. Bien qu'une telle brisure puisse être réelle dans les systèmes macroscopiques, elle n'est que fictive dans les systèmes quantiques finis, de sorte que l'obtention d'une solution exacte nécessite éventuellement de restaurer la symétrie brisée, c'est-à-dire rétablie le nombre spécifique de nucléons dans le cas présent. Cette tâche, qui a longtemps défié les théories à A corps, a été récemment réalisée par des théoriciens de l'Irfu/DPhN via le formalisme de la théorie dite « particle-number-projected Bogoliubov Couple Cluster » (PBCC) [1]. Dans ce formalisme, la symétrie U(1) est brisée pour autoriser une expansion significative et restaurée pour obtenir une solution de symétrie correcte qui prend en compte pleinement les corrélations fortes, c'est-à-dire la superfluidité.
La meilleure façon d'évaluer les performances d'une nouvelle méthode à A corps est de l'utiliser pour décrire un problème « type » dont les solutions exactes sont connues. C'est ce qui a été fait pour la théorie PBCC, en collaboration avec des chimistes quantiques de l'Université Rice [2] sur la base du célèbre problème d'appariement Bardeen-Cooper-Schrieffer (BCS) dont les solutions exactes ont été fournies il y a longtemps par Richardson [5]. Ce problème est parfaitement adapté étant donné que ses solutions passent, lors du réglage de la force d'interaction entre les particules du modèle, d'un état normal (faiblement corrélé) à un état superfluide (fortement corrélé). Comme l'illustre en figure 4, la nouvelle méthode PBCC (appelée Projected BCS-CC sur la figure) fournit des énergies des états fondamentaux quasi exactes pour toutes les forces d'interaction, ce qui représente une amélioration significative par rapport à la méthode BCC non projetée (appelée BCS-CC) ainsi que par rapport aux descriptions d'ordre zéro non projetées ou projetées (respectivement appelées BCS et Projected BCS). La méthode PBCC fournit ces résultats tout en conservant un coût polynomial à peine supérieur à celui de la méthode BCC non projetée.
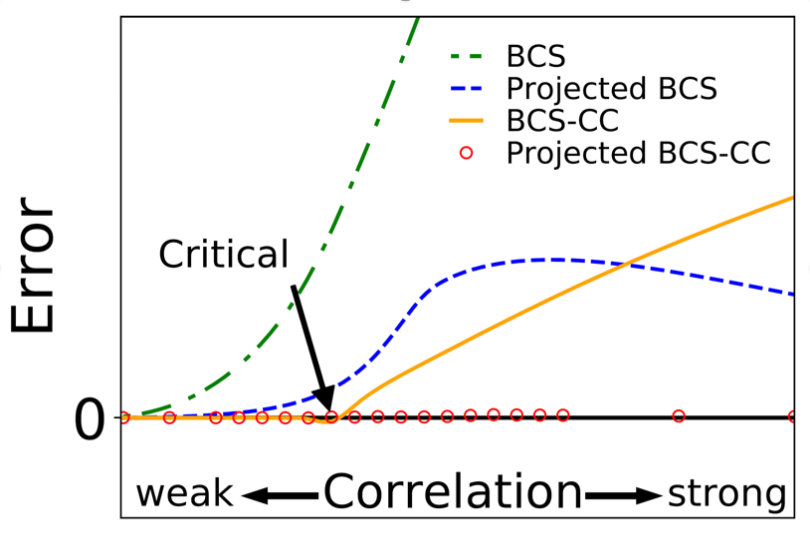
Figure 4 : Erreurs sur l’énergie fondamentale (unités arbitraires) par rapport à la solution exacte du problème de Richardson à A corps en fonction de la force d'interaction. Le point critique désigne la transition de phase entre la phase normale et la phase superfluide. Les méthodes polynomiales qui ne brisent pas la symétrie U(1) (résultats non représentés ici) ne peuvent pas donner de résultats sensibles dans la phase superfluide. L'avantage combiné de (i) briser la symétrie avant (ii) capturer les corrélations au-delà de la description à l’ordre ordre zéro puis (iii) restaurer la symétrie est clairement illustré.
En résumé, les théoriciens de l'Irfu/DPhN ont conçu et testé un nouveau formalisme pour les théories à A corps qui apporte des solutions très précises au problème de Richardson (problème qui peut être résolu exactement) et ce dans toutes les situations, qu'il s'agisse de faibles ou fortes corrélations. La prochaine étape consiste à mettre en œuvre cette méthode à A-corps pour calculer les propriétés ab initio des molécules et des noyaux atomiques indépendamment de leur caractère faiblement ou fortement corrélé.
[1] T. Duguet, A. Signoracci, J. Phys. G: Nucl. Part. Phys. 44 (2016) 015103
[2] Y. Qiu, T. M. Henderson, T. Duguet, G. E. Scuseria, Phys. Rev. C99 (2019) 044301
[3] V. Somà, C. Barbieri, T. Duguet, Phys. Rev. C87 (2013) 011303(R)
[4] A. Signoracci, T. Duguet, G. Hagen, G. R. Jansen, Phys. Rev. C91 (2015) 064320
[5] R. W. Richardson, Phys. Lett. 3 (1963) 277 ; Phys. Rev. 141 (1966) 949
• Structure de la matière nucléaire › Noyaux atomiques
• Institut de recherche sur les lois fondamentales de l'Univers (Irfu) • Le Département de Physique Nucléaire (DPhN)
