From the point of view of mathematical modelling, nothing looks more like an epidemic... than a nuclear reactor! While the link between these two "objects" may not be obvious at first sight, what they both have in common is that they involve the quasi-random movement of a species capable of reproducing and disappearing. In the case of an epidemic, this species is the infected individual who, as he or she moves around, may in turn infect other individuals. Once cured (or, more unfortunately, dead), the virus carrier disappears and no longer influences the spread of the epidemic. In the same way, but in 3 dimensions rather than 2, neutrons in a nuclear reactor move randomly and can give rise to other neutrons, through the fission mechanism, induced by the collision of neutrons on heavy nuclei (such as uranium 235). Sometimes escaping the reactor, or being captured during interactions with other nuclei composing the medium in which they are transported, neutrons also disappear and no longer contribute to the chain reaction taking place in the nuclear reactor core.
Branching Brownian motion and phase transition
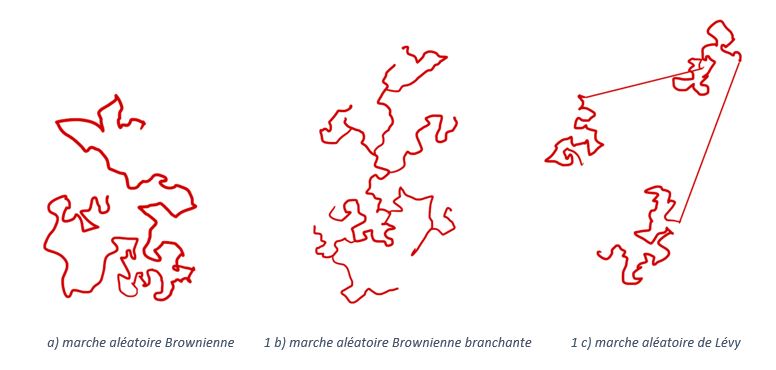
een from a distance, the random walk of neutrons follows a Brownian motion, in that it obeys the diffusion equation. The characteristic trajectories are erratic and noisy (see Figure 1.a): mathematicians describe them as continuous everywhere, but derivable nowhere. Nuclear power reactors are operated using this equation (or, to be more precise, using the diffusion equation with two groups of energies: one equation to describe the transport of fast neutrons, and another for slower, so-called thermal neutrons). In this way, the behavior of the neutron population in a reactor can be accurately modeled.
However, when the power in the reactor is stationary, the study of the chain reaction proves more delicate. Neutron scattering is termed "critical" because, under these conditions, a neutron gives rise, on average, to precisely one other neutron during its lifetime, but each interaction of a neutron with a heavy nucleus can potentially give rise to several "son" neutrons, resulting in branching trajectories. The study of branching Brownian motion (BBM for short), shown in Figure 1.b, was used some years ago to understand the onset phase of epidemics [1], and similar models were then used in neutronics to characterize the statistical fluctuations of the neutron gas. These can develop to the point where the gas no longer follows the diffusion law: this is known as a phase transition. In this "phase", the total neutron population can, in theory, become extinct or much larger than expected, leading ipso facto to a non-negligible increase in reactor power. In theory only, because in practice, recent research has shown that the total number of neutrons in the reactor fluctuates very little [2,3]. This surprising stability is due to the temperature effect: the higher the power (i.e. the number of neutrons) locally, the higher the temperature, and the more neutrons tend to be captured by the medium rather than inducing fission. This counter-reaction is due to the broadening of neutron resonances, which literally become neutron traps.
This counter-reaction, known as Doppler Broadening, is a lifesaver in that it stabilizes nuclear reactors in the power regime. On the other hand, the theoretical modelling of these effects becomes extremely delicate, if not impossible: the use of numerical codes coupling the resolution of neutron transport equations to that of temperature feedback equations becomes unavoidable. But these numerical methods themselves make assumptions whose legitimacy is difficult to assess...
And what about coffee?
In an attempt to describe this phenomenon, three researchers from a joint CEA-IRSN team noticed that the neutron gas at the critical point (when the chain reaction is stable) possessed exactly the same symmetry properties as a liquid filtered through a porous structure, such as water through the ground coffee in percolating coffee makers. In fact, it was possible to show that neutron trajectories at the phase transition point possessed a spatial scale invariance, characteristic of stochastic processes belonging to the universality class of directed (in time) percolation. As a result, the spatial and temporal fluctuations of the neutron field in the reactor, of importance to nuclear safety, could be calculated theoretically using renormalization methods (long-established results within the framework of quantum field theory).
The results of their work, published in the journal Physical Review E [4], brought to light some relatively surprising conclusions: the critical diffusion equation characterizing the neutron population becomes, in the presence of counter-reactions, a so-called super-diffusion equation, where the diffusive term usually given by a spatial derivative of order 2 in space then takes on a non-integer value, slightly less than 2! The microscopic generator of this equation (which describes the laws of neutron transport) is no longer a Brownian motion, but a Lévy random walk: the trajectories appear very similar to those of Brownian motion, with the exception of certain "jumps" projecting the neutrons a long way from their initial position (see Figure 1.c). As a result, the spatial distribution of power in the reactor is slightly modified (by a few percent), as shown in Figure 2, where the super-diffusion result is dotted and compared with that of simple diffusion. This is about the same order of magnitude as the accuracy expected from the calculation codes used in nuclear safety studies... So it seems that the safety ball is now in the numerical engineers' court!
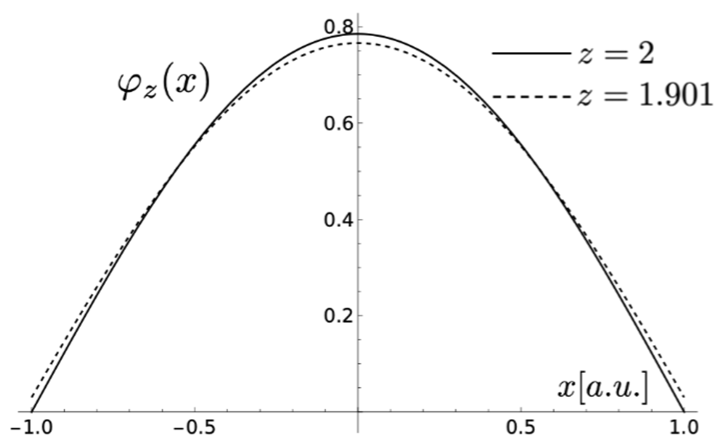
Spatial distribution (along the x axis) of the neutron population in a simplified reactor, symbolically located between -1 and 1. Solid line: neutron transport by a classical diffusion model (space derivative of order 2). Dashed line: neutron transport by a super-diffusion model given by a fractional space derivative of order 1.901.
Contact: E. Dumonteil
References
[1] Eric Dumonteil, Satya Majumdar, Alberto Rosso and Andrea Zoia, "Spatial extent of an outbreak in animal epidemics", PNAS 110 (11) 4239-4244 (2014) https://doi.org/10.1073/pnas.1213237110
[2] Fait marquant CEA 2022 "Rencontre entre la physique des réacteurs et la théorie des jeux" https://irfu.cea.fr/Phocea/Vie_des_labos/Ast/ast_visu.php?id_ast=4955
[3] Eric Dumonteil et al, "Patchy nuclear chain reactions", Nature Communications Physics volume 4, Article number: 151 (2021)
[4] Benjamin Dechenaux, Thomas Delcambre and Eric Dumonteil, "Percolation properties of the neutron population in nuclear reactors", Phys. Rev. E 106, 064126 (2023) https://arxiv.org/pdf/2210.02413.pdf