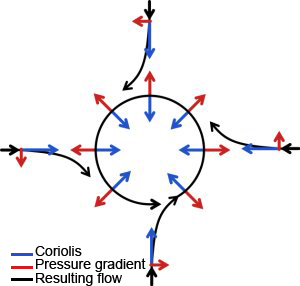
Rotation, represented by the symbol ?, occurs throughout the Universe (planets, planetary systems, stars, galaxies…). Its effect on a given element (solid object, fluid…) depends on the centrifugal force and Coriolis force. The former tends to drive any element away from the center. The latter’s effect is to deflect any moving object to the right in the northern hemisphere, to the left in the southern hemisphere. The faster the system rotates, the stronger centrifugal force will predominate, to the extent of completely tearing the object apart, should its amplitude exceed the object’s internal cohesion force, or forces. These internal cohesion forces would be, for instance, in a solid object, electrostatic forces between atoms, or, for a fluid mass such as a star, the force of gravity. The Sun rotates rather slowly (1 rotation in 28 days), compared to a dentist’s drill (3,000 rpm), or even related to other stars, some of which complete a rotation in under one day. Thus, its convective motions are mainly influenced by the Coriolis force. The most arresting effect of this force, undoubtedly, is the setting up of cyclones in the Earth’s atmosphere. A balance then prevails, between the horizontal pressure gradient and the Coriolis force: physicists speak of a geostrophic equilibrium. In stars, such “meteorological” phenomena also occur, however, just like on Earth, where cyclones invariably have a radius greater than about 100 km, the Coriolis acceleration only affects motions larger than a given scale, the so-called Rossby radius. In the Sun’s convective region, this radius stands somewhere between 10,000 and 30,000 km, allowing a separation to be effected, of scales sensitive to the effects of rotation from scales not so sensitive. Of course, the turbulent character of convective motions inside stars modifies this equilibrium. For instance, the meridional circulation (1) that is observed in the Sun results from just such a departure from geostrophy. For more rapidly rotating stars, centrifugal force becomes a major factor, and it then tends to flatten the star at the poles, turning it from a spherical shape to an ellipsoid.
(1) Meridional circulation: a mean flow in the form of cells contained in a meridional plane.