An important scientific program is devoted to the three-dimensional structure of the proton in particular its elementary constituents, quarks and gluons. A new generation of experimental facilities at Jefferson Lab (US), CERN, and perhaps later on at a future electron-ion collider (EIC), should make it possible to perform proton tomography with unprecedented accuracy. The success of this program depends on the extraction of quantities called generalized parton distributions (GPD) from a wide variety of observable sources. IRFU, in partnership with American, Spanish and Italian institutes, has taken a decisive step forward, by systematically building GPD models that comply with all the required theoretical constraints. These results are reported in two publications in high-impact journals Eur. Phys. J. C. [1] and Phys. Lett. B [2].
What can we do better than Rutherford in the last century?! This question was the subject of a round-table discussion on nucleon structure at a recent international conference [3]. This illustrates the richness of the theoretical and experimental developments of the last 20 years, and highlighted the promises of the new generations of experiences. In particular, the concept of generalized parton distribution (GPD) proposes to map the properties of the proton (probability of the presence of quarks and gluons, electrical charge distribution, etc.). These GPDs are already experimentally accessible, especially when the proton is probed via the Deeply Virtual Compton Scattering (DVCS). This channel, in which an electron (or muon) interacts with a proton to produce an electron (or muon), a photon and a proton in the final state [4], is studied by IRFU's teams at Jefferson Lab and CERN.
From a phenomenological point of view, the difficulty of this task lies in the fact that the GPDs are not the quantities that are directly measured. The link between observables and GPDs is complex but under good theoretical control. This is therefore an inverse problem, that physicists generally solve by choosing a functional form of the GPD to be extracted from the data, which depends on a number of parameters whose values are then adjusted to best reproduce the experimental signals. However, the specificity of GPDs is that they must obey a large number of constraints resulting from primary physical principles. These constraints are strong enough to exclude naive parameterizations, but too weak to result in a single description of the GPDs. Since 2002, physicists have attempted extractions, either by neglecting some of the theoretical constraints required or by relying on functional forms that are too rigid to accommodate experimental data. This led to systematic effects that were acceptable in terms of the accuracy of the first DVCS measurements, but unsustainable in the era of accuracy that is beginning to emerge.
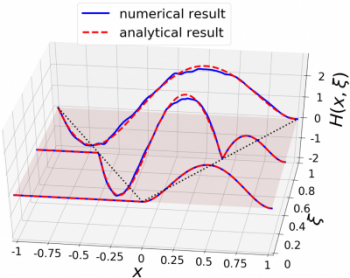
Fig. 1: The GPD H(x, ?) where x and ? refer to fractions of the momentum of the pion carried by the so-called "active" quark, i. e. the one that interacts with the incident electron or muon of the DVCS process. The red curve corresponds to a perfectly known model, and the blue curve to a numerical calculation implementing the theoretical constraints on GPDs based on the knowledge of the initial model in the domain x > ? . The agreement between the test model and its reconstruction from sample data is excellent.
At the cost of a modelling effort started at the end of 2014, and an original approach, it was possible to solve this problem that has been open for about fifteen years. The solution involves reversing a well-known mathematical transformation in medical tomography, the Radon transformation. In transmission tomography, a section of human body is scanned by a narrow beam of X-rays whose loss of intensity is recorded by a detector. The Radon transformation mathematically describes the loss of intensity along the direction of beam propagation, and the inversion of the Radon transformation delivers the two-dimensional images that are used by physicians to make their diagnosis. How to make the link with our problem of GPD modeling? The principle of the solution consists in building a GPD in a flexible way, with parameters that will later be adjusted to the experimental data, on a subset of its definition domain. By reversing the Radon transformation, it is possible to extend this functional form to the entire definition domain by ensuring compliance with the primary physical principles. The solution to the GPD modelling problem therefore combines considerations of nuclear physics, functional analysis and analytical calculation. The obtained algorithm allows the systematic construction of functional forms satisfying a priori all the good theoretical properties, independently of the value of the free parameters to be adjusted to the experimental data. This algorithm has been successfully tested on several representative cases. The aim was to verify that it was possible, with a single algorithm, to reproduce the few known special cases of GPD models while respecting the primary physical principles for each of them (Fig. 1).
This theoretical breakthrough opens new doors and is not limited to the structure of the nucleon. An immediate application of this new approach to the case of the pion (the lightest states consisting of a quark and an antiquark) allowed a significant improvement of an ab initio model developed in 2015 and which had been the subject of a former highlight.
References
[1] N. Chouika et al., Eur. Phys. J. C77 (2017) 906.
[2] N. Chouika et al., Phys. Lett. B780 (2018) 287.
[3] N. Stefanis et al., EPJ Web Conf. 137 (2017) 01003.
[4] K. Kumeri?ki et al., Eur. Phys. J. A52 (2016) 157.
Contacts : Nabil CHOUIKA et Hervé Moutarde
• Structure of nuclear matter › Quarks and gluons hadron structure
• The Nuclear Physics Division
• Nucleon Structure Laboratory (LSN) - The internal structure of hadrons



