A recent theoretical study of the IRFU has overturned a dark matter mechanism claiming to explain the anomaly in the neutron lifetime. Indeed, the strong constraints, extracted from this mechanism, make it impossible to theoretically predict the neutron stars of 2 solar masses whose existence is known. This study was conducted in collaboration with physicists from the University of Adelaide in Australia, and will soon be published in the journal J. Phys. G. Based on theoretical calculations of nuclear physics, combined with astronomical observations, this case illustrates well the fertility of transverse approaches in physics.
The nature of dark matter remains mysterious despite intense research over the past several decades. By definition, these particles undergo gravitation and do not interact with photons. This explains why galaxies rotate faster than allowed by their visible mass. In addition, we know that they are neutral particles and that they are not part of the standard model.
In this context, it is understandable that new ideas are welcome and the one proposed very recently by Fornal and Grinstein [1] was rather original. Indeed, the neutron disintegrates according to the process:
n → p + e– + νe (1)
and we know that the lifetime of the neutron is slightly longer when measured by detecting the proton from disintegration than when it is measured inclusively, i.e. by studying the rate of neutron disappearance. Their interpretation was that in the inclusive case a disintegration channel to a dark matter particle, named χ in the following, has to be taken into account. Obviously, this mechanism seems to contradict some basic knowledge. For example, what prevents stable nuclei from acquiring a dark matter component as they disintegrate? On the other hand, since dark matter is not in the standard model, the transition n → χ violates the conservation of the baryonic number. Fornal and Grinstein have shown that these objections do not hold if the mass of the dark matter particle satisfy 937.9 MeV < mχ < mn because the problematic transitions are then kinematically forbidden. When we know that even the order of magnitude of mχ is not known, such a constraint would be precious for direct research.
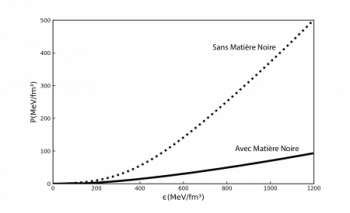
Pressure as a function of energy density, i.e., the equation of state, calculated in the QMC model with and without dark matter.
In the allowed range, there are 2 possible types of disintegration. A first experiment has already eliminated the transition n → χ + γ [2] and there is still the possibility n → χ + χ′ where χ′ is a light dark matter particle. This channel is much more difficult to exclude and this is where neutron stars come to the rescue [3, 4, 5].
These residues of the gravitational collapse of massive stars (supernovae type II) have a mass that can reach 2 solar masses [6] and a radius of 15 km or less. The density at the center is 5 to 10 times higher than the one that exists in the nucleus of atoms and the temperature at the surface after 1 million years is about 1 million degrees. At a depth of a few hundred meters, the density is such that the atomic nuclei are dissolved into a uniform nuclear matter that is similar to what exists inside the nuclei. The difference is that, on the one hand, the density can be much higher, and on the other hand, this material contains mostly neutrons, hence the name. The charge of the small fraction of protons is canceled out by electrons or muons.
The resistance to gravitational force is provided by the pressure of the material. Qualitatively, on the one hand, we have the pressure of a neutron gas at zero temperature and whose origin is simply the velocity of the various particles. It exists independently of interactions. On the other hand, there is the repulsion at short distance between neutrons, the famous hard core of the nuclear force. The latter dominates at very high density and allows for the existence of neutron stars with up to 2 solar masses rather than black holes.
Now suppose that the neutrons of the star are allowed to disintegrate into dark matter. A new balance will gradually be established and we can guess what will happen. First, the neutron density will decrease in favour of dark matter and the pressure loss on the neutron side is not compensated by that of dark matter. Secondly, the effect of short-range repulsion will be reduced because dark matter is not affected by this interaction. Both effects are added and lead to a reduction of the pressure.
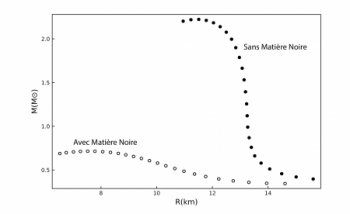
These arguments are of course qualitative. To draw quantitative conclusions, a realistic model is used to calculate the equation of the state of matter, i.e. the relationship between pressure and density. Here we use the QMC model [7] which describes well ordinary nuclei and at the same time predicts neutron stars, particularly the one observed of 2 solar masses. Figure 1 shows the equation of state and as expected we see that the presence of dark matter considerably reduces the pressure. The consequence for the mass of neutron stars is spectacular, as shown in Figure 2. The maximum mass reaches barely 0.7 solar mass, which is contradicted by the observations. We can therefore conclude that the scenario proposed by Fornal and Grinstein to explain the anomaly in the neutron lifetime is excluded.
This case illustrates perfectly the unity of physics and the fertility of transversal approaches. The concept of dark matter, derived from astronomical observations, is not part of the standard model of particle physics. However, a scenario invoking this dark matter could explain the disagreement between two measurements of the neutron lifetime. Theoretical calculations of nuclear physics, combined with astronomical observations, make it possible to reject this scenario. This type of approach may foreshadow approaches that will be common in the future as neutron stars have just entered the observational domain of gravitational waves.
References
1. [1] B. Fornal and B. Grinstein, “Dark Matter Interpretation of the Neutron Decay Anomaly,” arXiv:1801.01124 [hep-ph].
2. [2] Z. Tang et al., “Search for the Neutron Decay n → X + γ where X is a dark matter particle,” arXiv:1802.01595 [nucl-ex].
3. [3] T.F. Motta, P.A.M. Guichon and A.W. Thomas, “Implications of Neutron Star Properties for the Existence of Light Dark Matter,” à paraître dans J. Physics G, arXiv:1802.08427 [nucl-th].
4. [4] G. Baym, D.H. Beck, P. Geltenbort and J. Shelton, “Coupling neutrons to dark fermions to explain the neutron lifetime anomaly is incompatible with observed neutron stars,” arXiv:1802.08282 [hep-ph].
5. [5] D. McKeen, A.E. Nelson, S. Reddy and D. Zhou, “Neutron stars exclude light dark baryons,” arXiv:1802.08244 [hep-ph].
6. [6] P. Demorest, T. Pennucci, S. Ransom, M. Roberts and J. Hessels, “Shapiro Delay Measurement of A Two Solar Mass Neutron Star,” Nature 467 (2010) 1081 ,arXiv:1010.5788 [astro-ph.HE].
7. [7] P.A.M. Guichon, J.R. Stone and A.W. Thomas, “Quark–Meson-Coupling (QMC) model for finite nuclei, nuclear matter and beyond,” Prog. Part. Nucl. Phys. ,arXiv:1802.08368 [nucl-th].
Contact : P.A.M. Guichon
• Structure of nuclear matter › Quarks and gluons hadron structure
• The Nuclear Physics Division
• Nucleon Structure Laboratory (LSN) - The internal structure of hadrons