A new window into the deformation of nuclei has been recently opened with the realisation that nuclear collision experiments performed at high-energy colliders, such as the BNL Relativistic Heavy Ion Collider (RHIC) or the CERN Large Hadron Collider (LHC), give access to the shape of the colliding isotopes. A collaboration between high- and low-energy theorists, including researchers from IRFU, has demonstrated that quantitative information on nuclear deformations can be obtained and has shown that the isotope 129Xe appears as triaxial, i.e. a spheroid with three unequal axes. This result represents the first evidence of triaxiality in nuclear ground states attained in high-energy experiments. Moreover, it opens the way to exciting future investigations at the interface of low- and high-energy nuclear physics.
The interpretation of the emergent collective behaviour of atomic nuclei in terms of deformed shapes is at the heart of our understanding of their diverse properties, giving rise to a large variety of phenomena ranging from nuclear energy to astrophysical processes over a wide spectrum of energy scales. Experimentally, nuclear deformation is traditionally studied via low-energy collision measurements. Recently, however, it was realised that one can access the shape of nuclei also in high-energy ion collision experiments.
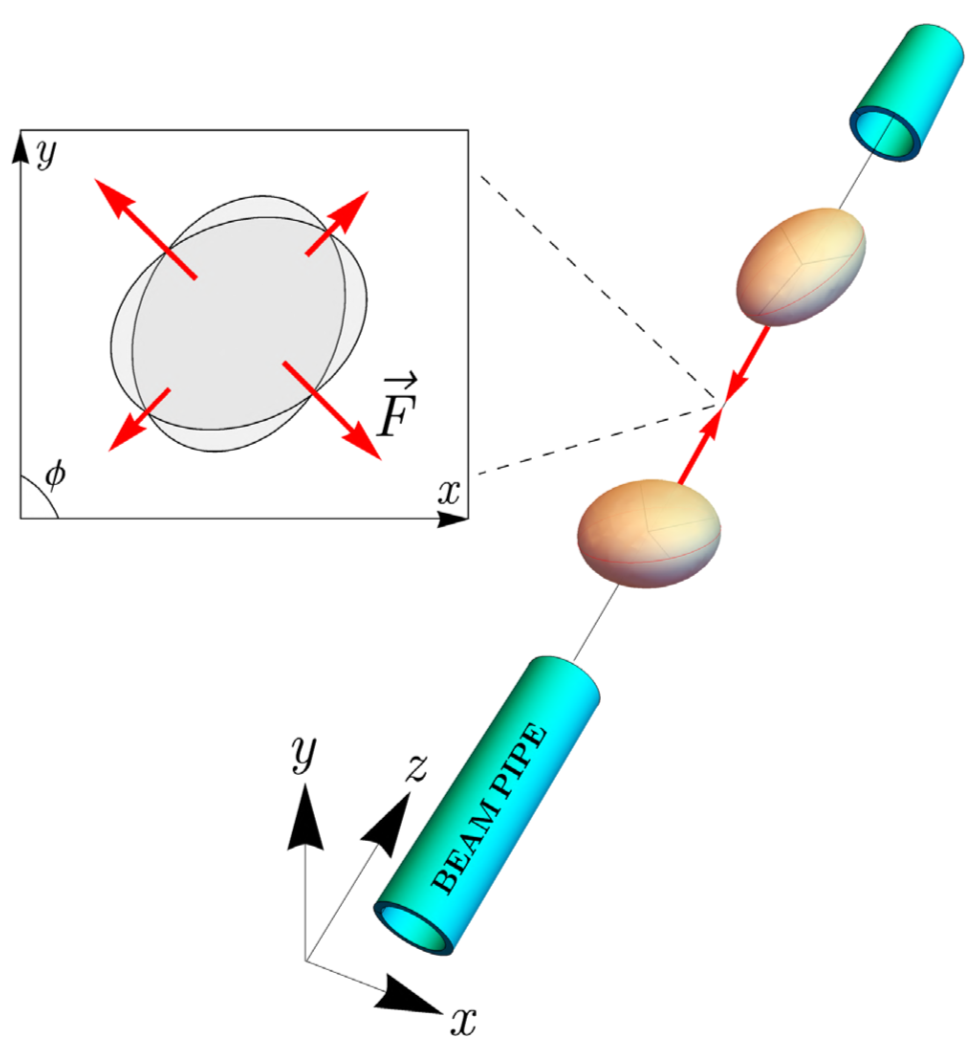
Figure 1. Illustration of a head-on collision between two atomic nuclei performed in a collider experiment. The nuclei, deformed in their ground state, are randomly oriented as they run in the beam pipe, and the shape of their area of overlap can range from circular to elliptical. The expansion of this medium in the plane perpendicular to the beam (x,y) is driven by a force field F, which carries the same anisotropy as the overlap area. Note that in the frame of the laboratory the two nuclei would look like thin pancakes, squeezed in the beam direction z, due to a strong effect of Lorentz contraction.
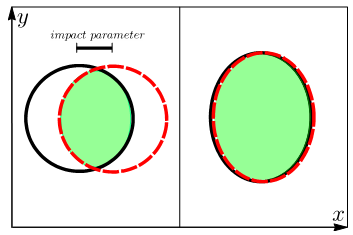
Figure 2. Anisotropic overlap regions in nuclear collisions. Left: a collision of spherical nuclei breaks anisotropy in the transverse plane due to the finite impact parameter. Right: a central collision of deformed nuclei breaks anisotropy due to the non-spherical shape of the colliding bodies.
Indeed, in such collisions, the geometry plays a crucial role. As shown in Fig. 1, when colliding two deformed nuclei, the overlapping area geometry will be constrained by the geometry of the two nuclei. If this area is not a disk but an ellipse, it will trigger a deformation of the distribution of hadrons in the plane perpendicular to the beam, which is detected in the final state of the collision. This deformation of the hadron distribution is called the elliptic flow and can be connected to the initial asymmetry of the interaction area. Nuclear deformation may however not be the only source of elliptic flow. As illustrated in Fig. 2, in the case of spherical nuclei, but non-central collisions (left-hand side), the interacting region is deformed and generates an elliptic flow. Therefore, selecting most central events is crucial to investigate the shape of nuclei.
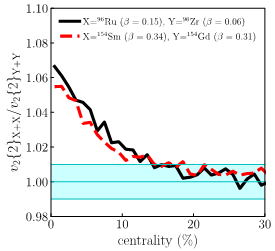
Can one translate these geometric considerations into quantitative estimates? It turns out that collisions of isobars (i.e., nuclides with different number of protons but the same number of nucleons) allow to do so very cleanly. Indeed, if the two nuclides are characterized by the same shape and the same number of nucleons, the same elliptic flow will be produced in the collisions, and the ratio of elliptic flows will be equal to one. On the contrary, any significant deviation from unity points to different initial deformations of the two nuclei. In particular, the collaboration has demonstrated that such deviation can be related to specific shape parameters of the two isobars [1]. Monte Carlo simulations have then confirmed that the effect is sizeable and provided predictions for two sets of isobaric collisions, namely 96Ru vs 96Zr and 154Sm vs 154Gd (see Fig. 3, where the ratios indeed significantly grow above one towards zero centrality, i.e. for head-on collisions). Recently, the STAR collaboration (one of the RHIC detectors at Brookhaven, USA) has released experimental data on the former case that confirm this prediction.
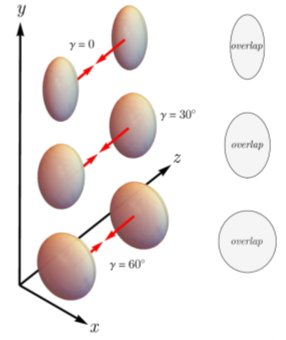
Figure 4. Head-on collisions at small values of the mean transverse momentum of detected hadrons permit one to isolate configurations that maximize the overlap area. Depending on the value of the angle controlling the length imbalance of the axes of the deformed spheroid (labelled ?), collision configurations at low mean hadron transverse momentum can thus vary between geometries that maximally break azimuthal symmetry (?=0°) and geometries that are azimuthally symmetric (?=60°).
Shortly afterwards, another breakthrough was achieved based on the realisation that the mean momentum of the produced hadrons (again, in the plane perpendicular to the beam) can be used to gauge the relative orientation of the two nuclei at the collision point. For collisions of a given (deformed) isotope, this can be exploited to select events in which the overlap area is maximal. Crucially, the shape of this overlap area will be different depending on whether the nucleus has a prolate, oblate or triaxial deformation (the latter denoting a spheroid with three unequal axes, see Fig. 4).
As a consequence, the observed elliptic flow allows us to distinguish between these possibilities, i.e., to determine the parameter γ controlling the length imbalance of the axes of the deformed spheroid. This parameter varies from 0° (prolate shape) to 60° (oblate shape). The theorists from Irfu, Madrid, Lyon and Heidelberg have verified these findings by performing state-of-the-art nuclear structure calculations of the nucleus 129Xe and subsequent Monte Carlo simulations for relativistic collisions of these isotopes [2]. The results are shown in Fig. 5 and a clear difference in the considered observable (here the Pearson correlator) can be seen between oblate nuclei (dotted blue curve) and prolate nuclei (dot-dashed green curve). Triaxial configurations sit in between (dashed red curve), while the solid black curves correspond to the result obtained for a spherical nucleus, 208Pb.
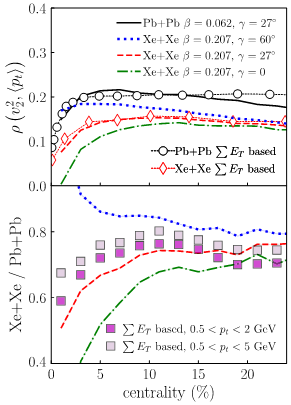
Figure 5. Theoretical and experimental results on the correlation between elliptic flow and the mean transverse momentum. Symbols are preliminary measurements from the ATLAS (CERN) collaboration. Upper: the centrality dependence of the Pearson correlator coefficient in both 208Pb-208Pb and 129Xe-129Xe collisions. Lower: their ratio.
Comparing the theoretical results with preliminary data from the ATLAS collaboration at CERN [3] indicates that 129Xe has a triaxial shape (see Fig. 5), with deformation parameters compatible with those of the neighbouring 130Xe as determined by a recent low-energy experiment [4]. This result represents the first evidence of triaxiality in nuclear ground states attained in high-energy experiments. Moreover, it opens the way to exciting future investigations at the interface of low- and high-energy nuclear physics.
References
[1] G. Giacalone, J. Jia, V. Somà, Phys. Rev. C 104 L041903 (2021)
[2] B. Bally, M. Bender, G. Giacalone, V. Somà, Phys. Rev. Lett. 128 082301 (2022)
[3] The ATLAS collaboration, arXiv:2205.00039 (2022)
[4] L. Morrison et al., Phys. Rev. C 102 054304 (2020)
Contacts