Prediction of nuclear properties based on a realistic description of the strong interaction is the main quest of low-energy nuclear theory. One of the issues lies is the cost of solving Schrödinger’s equation that scales exponentially with the number of nucleons. Consequently, theoretical predictions based on first principles have long been limited to very light nuclei, to nuclei with specific proton and neutron numbers offering simplifications or to their ground states. While releasing each of these three constraints separately is ongoing, overtaking them at the same time constitutes the current forefront in the field. Employing a novel many-body formalism [1] recently developed by the PAN@CEA (“Problème à N corps au CEA”) collaboration (DRF-DAM-DES), the calculation of collective excitations, i.e. nuclear rotations and vibrations, in all medium-mass nuclei is envisioned for the first time [2,3]. This work paves the way to large-scale predictions of nuclear properties from first principles.
An atomic nucleus is composed of A nucleons, i.e., Z protons and N neutrons, whose interactions result from strong interactions of quarks and gluons inside them, described within the theory of Quantum Chromo Dynamics (QCD). Based on nucleons and their interactions, predicting nuclear properties from first principles requires to solve the A-body Schrödinger’s equation. The physicists denote these predictions as “ab initio”, which in latin means “from the beginning”. This can only be done numerically, without the need of approximations, for very light systems with A ? 16. Given that the associated cost grows exponentially with A, the description of heavier nuclei requires the design of efficient approximate methods, thus making the computing cost grow as a polynomial rather than as an exponential function of A. Still, the appropriateness and complexity of a given approximation method eventually depends on whether the nucleus under consideration is weakly or strongly correlated, which in turn depends on the specific proton and neutron numbers, as explained in the following. Correlations among the nucleons result from their interactions and measure how much their behaviour inside the nucleus differ from a vision where they would evolve independently from one another in a common average potential (i.e. “mean-field” picture/approximation). The stronger the correlations, the harder it is to design accurate approximations to solutions of A-body Schrödinger’s equation.
Weak (“dynamical”) and strong (“static”) correlations
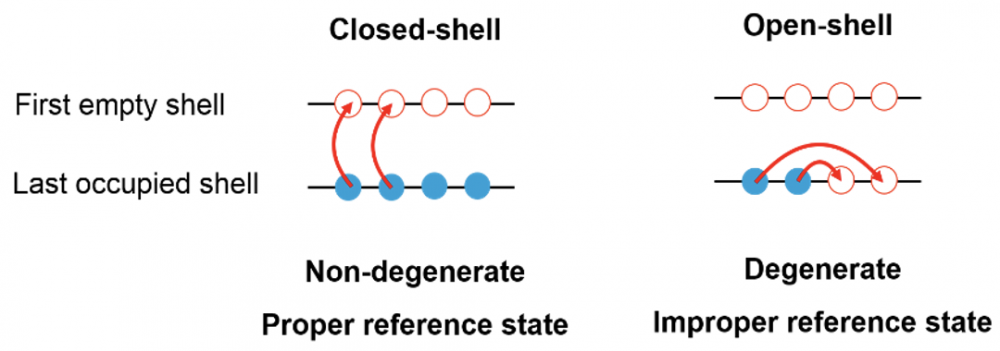
The fact that a nucleus displays strong “static” correlations in addition to weak “dynamical” correlations is empirically related to the picture at play in the “mean-field” description of the system one starts from before adding the needed nucleonic correlations on top of it. In this description, protons (neutrons) are simply occupying the Z (N) lowest quantum levels or “shells” associated with the mean-field whose degree of degeneracy, i.e., the maximum number of protons (neutrons) they can accommodate, is dictated by the rotational symmetry of the system. If Z (N) is such that the highest occupied shell is fully filled, the system is said to be of proton (neutron) “closed-shell” character. Otherwise, the system is proton (neutron) “open-shell”. The two situations are schematically illustrated in Fig. 1.
Whenever the nucleus is of doubly closed-shell character in the mean-field approximation, the only possible transitions induced by inter-nucleon interactions relates to nucleons “jumping” across the empty gap to a higher energy level (fig. 1 left panel). Because the presence of the gap hinders these excitations, the nucleus only display weak (so-called “dynamical”) correlation among the nucleons. In about 90% of the time, however, the nucleus is singly or doubly open-shell and further displays another type of correlations: interactions between the nucleons can easily induce nucleonic transitions within the same energy shell. These transitions induce so-called strong “static” correlations among nucleons that are collective in nature, since many nucleons contribute coherently at once. To acquire a systematic understanding of nuclei and to deliver consistent and reliable nuclear data, it is thus mandatory to develop many-body methods capable of tackling both weak and strong correlations at once.
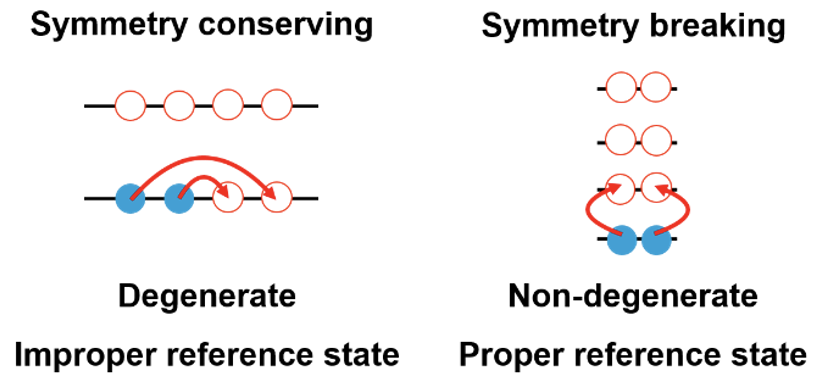
Figure 2: Schematic shell sequence and shell filling for an open-shell nucleus in a symmetry-conserving (left) and a symmetry-breaking (right) zeroth-order description.
Expanding and approximating the exact solution
1) Computational cost reduction
For closed-shell nuclei, techniques already exist to incorporate dynamical correlations on top of the mean field description at moderate computational cost. While uncorrelated nucleons occupy a closed-shell configurations of a mean field obeying rotational invariance, dynamical correlations are introduced on top of this description by allowing nucleons to excite to higher energy states (see fig. 1). Such techniques are rather accurate (2% error) but fails for open shell nuclei where strong correlations are further present. Therefore, research activities have more recently focused on the design of novel formalisms that can be universally applied to A-body systems with 2 ≤ A ≤ few hundreds, independently of the fact that they are weakly or strongly correlated.
2) From weakly to strongly correlated nuclei
Whenever the system is of neutron and/or proton open-shell character, nucleons can be reshuffled by their interactions within the open shell at zero energy cost (see right panel of Fig. 1). This makes the previous description based on a single rotationally invariant mean-field state corrected by correlations induced by transitions across an empty energy gap to break down. A way to bypass this issue is to allow the initial mean-field state to break rotational symmetry, even though the final description shall respect such a symmetry.
Lowering the symmetry requirements lifts the problematic degeneracy present in the initial mean field state such that the system effectively recovers a closed-shell character, as schematically illustrated in Fig. 2. Whereas such a new symmetry-breaking mean-field state already captures strong “static” correlations, dynamical correlations associated with nucleonic transitions across an empty gap can be safely added as previously. Note that if open-shell nuclei necessitate a symmetry-breaking mean-field state, closed-shell ones do not even if allowed to. The system decides for itself such that all types of nuclei can be consistently treated within the same approach. Over the past few years, theoreticians of the PAN@CEA collaboration have developed several methods to solve A-body Schrödinger’s equation while allowing the mean-field state to break both particle-number and rotational symmetries [4], producing in particular the first systematic ab initio calculations of mid-mass singly open-shell nuclei [5].
While having made possible to go beyond the state of the art, these novel many-body formalisms still come with two limitations:
- Although the handy breaking of symmetries can be real in macroscopic systems, it is only fictitious in a finite quantum system such as the atomic nucleus. Consequently, obtaining an accurate and fully satisfactory solution eventually requires the restoration of the symmetries that have been conveniently broken in the design of the initial mean-field state.
- Approximate methods to solve Schrödinger’s equation are first formulated to address nuclear ground states and can typically be extended to only access non-collective excitations, i.e. not originating from many nucleons at once.
Symmetry restoration and ab initio description of nuclear collective excitations
Addressing limitations 1. and 2. listed above at a limited (polynomial) computing cost constitutes a long-term challenge in many-body theory. This challenge has recently been taken up by theoreticians of the PAN@CEA collaboration by replacing the mean-field states discussed above by a more elaborate state obtained via the so-called projected generator coordinate method (PGCM) and by formulating a method to consistently add dynamical correlations on top of it [1]. The PGCM acts as a symmetry restorer: from one symmetry-broken or deformed state found previously, it generates all other non-symmetric states via the application of symmetry transformations. By further combining all these non-symmetric states, the PGCM is able to build a composite state fulfilling the required symmetries, thus cleaning the system from fictitious symmetry breaking. From that state, it is possible to apply a carefully designed method to add dynamical correlations. Eventually, the new method can
- tackle strong static collective correlations and weak dynamical correlations consistently
- maintain good symmetries all throughout
- access ground state properties as well as collective rotational and vibrational excitations
As an example, Fig. 3 compares the ab initio prediction of the ground-state rotational band in the doubly open-shell 20Ne nucleus to experimental data [3] (left panel) and displays a typical cross section (the integrated isovector electripole dipole photo-absorption cross section σIVD(ω)) in 18-32Ne [6] (right panel). This cross section is related to specific vibrational excitations of the nucleus that have only been computed ab initio in doubly closed-shell nuclei so far. The calculations are based on state-of-the-art two-nucleon and three-nucleon interactions rooted into QCD. This first set of theoretical calculations highlighted very interesting outcomes. Among them, it showed that weak dynamical correlations brought on top of the PGCM state, while being crucial to describe absolute energies, essentially cancel out in collective excitation spectra as those reported in Fig. 3.
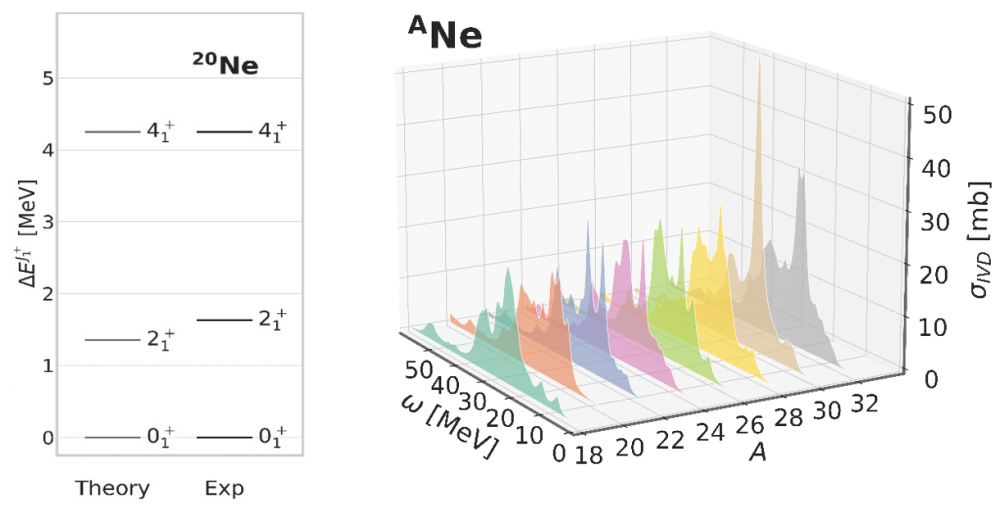
Figure 3: Ab initio calculations of nuclear collective excitations. Left Panel: excitation energy of the low-lying members of the ground-state rotational band in 20Ne (Z=10, N=10). Right panel: integrated isovector electripole dipole (IVD E1) photo-absorption cross section in eight consecutive even-even Ne isotopes (N=8 to N=22). The latter observable relates to specific vibrational excitations of the nucleus and is a key ingredient for radiative capture cross-section evaluations useful to nucleosynthesis models as well as reactor applications.
In summary, theoreticians of the PAN@CEA collaboration have designed and tested a novel ab initio many-body formalism providing, at reasonable computational cost, access to nuclear ground states and collective excitations independently of the doubly closed-shell, singly open-shell or doubly open-shell character of the system under consideration. The chosen path goes through symmetry breaking and symmetry restoration, the price to pay being a composite mean field state. But this price is clearly worth paying as it opens up for the first time the path towards first-principle large-scale predictions of collective excitations that are not only relevant for the fundamental understanding of nuclei but also for nuclear applications of interest at CEA.
References
[1] M. Frosini, T. Duguet, J. P. Ebran, V. Somà, Eur. Phys. J. A58 (2022) 62
[2] M. Frosini et al., Eur. Phys. J. A58 (2022) 63
[3] M. Frosini et al., Eur. Phys. J. A58 (2022) 64
[4] V. Somà, T. Duguet, C. Barbieri, Phys. Rev. C84 (2011) 064317 ; T. Duguet,
J. Phys. G: Nucl. Part. Phys. 42 (2015) 025107 ; A. Signoracci, T. Duguet, G. Hagen, G. R. Jansen,
Phys. Rev. C91 (2015) 064320 ; T. Duguet, A. Signoracci, J. Phys. G: Nucl. Part. Phys. 44 (2016) 015103 ; A. Tichai, P. Arthuis, T. Duguet, H. Hergert, V. Somà, R. Roth, Phys. Lett. B786 (2018) 195 ; A. Tichai, P. Arthuis, H. Hergert, T. Duguet,
Eur. Phys. J. A58 (2022) 2
[5] V. Somà, C. Barbieri, T. Duguet, Phys. Rev. C87 (2013) 011303(R)
[6] M. Frosini et al., unpublished
Contact
Thomas Duguet, CEA-Saclay/Irfu/DPhN/LENA