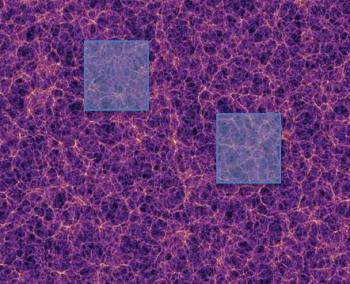
Figure 1 : Dans cette simulation, où chaque point est une galaxie, l’univers apparaît avec une structure filamentaire à grande échelle. La densité moyenne dans deux boites différentes de 1 milliard d’années-lumière de coté est la même. Il est homogène à très grande échelle.
L’homogénéité de l’Univers est l’un des fondements de la cosmologie. Des chercheurs de l’Irfu ont réalisé une cartographie de l’Univers en 3D grâce au relevé de quasars de SDSS III (Sloan Digital Sky Survey). Ils ont ainsi pu vérifier cette hypothèse pour des échelles plus grandes que le milliard d’années-lumière. Cette étude n’est pas un simple test de cohérence, contrairement aux précédentes, c’est-à-dire qu’elle ne repose pas au départ de façon implicite sur l’homogénéité pour la démontrer à la fin. Elle a été publiée dans Journal of Cosmology and Astroparticle Physics, Volume 2016, November 2016.
Le principe cosmologique
La cosmologie se fonde sur le principe cosmologique, qui stipule que l’Univers est isotrope, le même dans toutes les directions, et homogène, le même en tout point. Mais, direz vous, quand j’observe le ciel à l’œil nu, il ne m’apparaît pas isotrope, les étoiles se regroupent dans la voie lactée. L’Univers est effectivement anisotrope à petite échelle, mais à une échelle de l’ordre du milliard d’années-lumière il serait isotrope et homogène, comme illustré sur la figure 1. Mais en est-on sûr ?
Tester l’homogénéité
La méthode la plus directe pour tester l’homogénéité de l’Univers et d’en réaliser une cartographie en 3D. Mais la tâche est délicate. Il faut bien réfléchir aux hypothèses cachées. Ainsi les études précédentes à partir de cartographies 3D testaient l’homogénéité en la présupposant car pour transformer les observations (positions angulaires et décalage vers le rouge) en distances, elles utilisaient une « métrique FLRW[1] » qui suppose l’homogénéité. Elles n’étaient que des tests de cohérence de l’hypothèse d’homogénéité.
Ici au contraire on fait appel à un théorème rigoureusement démontré pour prouver l’homogénéité à partir des seules observations et du Principe de Copernic. Celui-ci stipule que nous ne sommes pas à un endroit particulier de l’Univers.
Les limites de la cartographie 3D
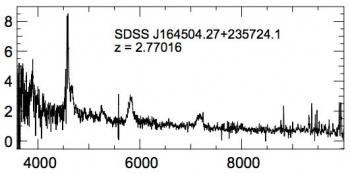
L’idéal serait de cartographier la densité totale de matière dans l’univers. Mais on ne peut cartographier qu’un type de sources donné. On peut mesurer les spectres de ces sources (par exemple des quasars, voir Figure 2). On en déduit leur décalage vers le rouge (Figure 5) et donc la distance à laquelle se trouvent ces sources. Un tel relevé fournit donc une cartographie en 3D et permet de montrer que la densité des sources est constante à grande échelle, ρs(r,θ,Φ)=constante.
Mais le rapport entre la densité de sources et la densité totale de l’Univers peut varier au cours du temps pour des raisons astrophysiques. Et comme lorsque l’on regarde loin on regarde dans le passé, cela signifie que ρs(r)/ ρtot(r) n'est pas constant. Ainsi ρs(r,θ,Φ)=constante implique seulement ρtot(r,θ,Φ)= ρtot(r) et pas ρtot(r,θ,Φ)=constante
Figure 2 : Le spectre d’un quasar de SDSS. La position des pics permet de déterminer le décalage vers le rouge du quasar.
Figure 3 : Le télescope Sloan à Appache point, au nouveau Mexique.
Isotropie et homogénéité
Cette propriété, ρ(r,θ,Φ) = ρ(r), est dénommée « isotropie spatiale », elle signifie que c’est isotrope pour chaque valeur de r prise séparément. Il existe un théorème qui dit que, combinée avec le principe de Copernic, elle implique l’homogénéité, ρ(r,θ,Φ) = constante. Dans ce contexte le principe de Copernic signifie simplement que puisque nous observons un Univers spatialement isotrope autour de notre position, c’est également le cas pour un autre observateur à quelques milliards d’années-lumière. De plus, on peut établir cette isotropie spatiale à partir des seules observations sans devoir les transformer en distance, donc sans faire appel à une métrique FLRW qui suppose implicitement l’homogénéité.
L’isotropie spatiale est une contrainte plus forte que la simple isotropie vérifiée avec d’autres types d’observations qui ne font pas de cartographie en 3D, comme le rayonnement fossile du Bigbang qui permet de tester l’isotropie à une distance donnée, ou la distribution angulaire des galaxies radio et le fond de rayons X dont les observations sont moyennées sur une plage de distance. Il est possible d’imaginer des contre-exemples qui montrent que le théorème n’est pas vrai pour cette simple isotropie.
Les observations de SDSS (Sloan Digital Sky Survey)
Les physiciens de l’irfu ont défini cette nouvelle façon d’analyser les cartographies en 3D pour l’appliquer aux 160 000 spectres de quasars mesurés par la collaboration BOSS au sein de SDSS. Ils ont ainsi pu établir l’homogénéité de l’Univers pour des échelles supérieures à 1 milliard d’années-lumière (voir Figure 4).
Les quasars sont des sources astrophysiques très lumineuses et donc détectables sur une large gamme de temps jusqu’à la jeunesse de l’Univers (ici entre z =2.2 et z =2.8).
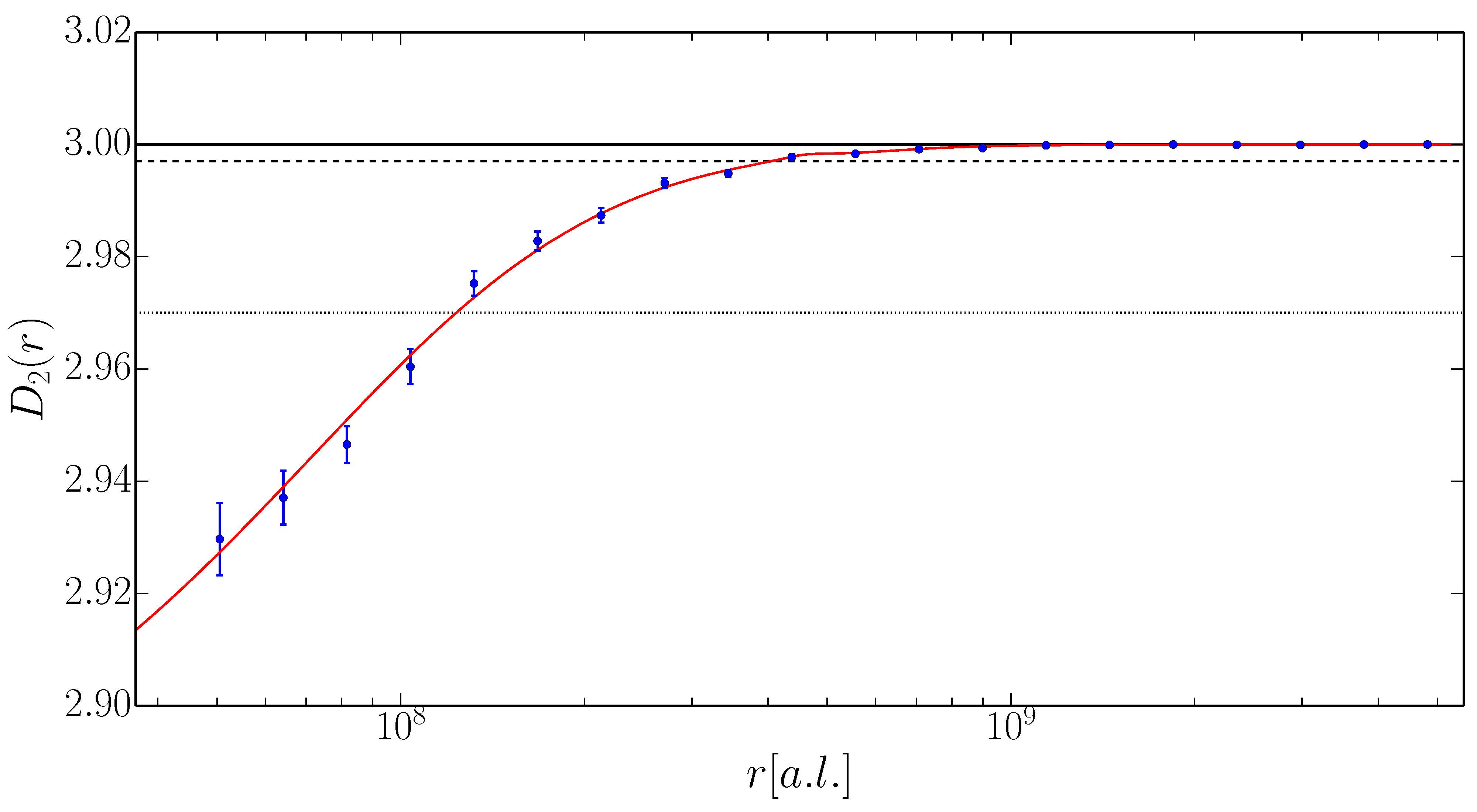
Figure 4 : Les physiciens mesurent la « dimension de corrélation fractale » de l’Univers qui vaut 3 si l’Univers est homogène. On voit que c’est le cas à partir d’une échelle d’environ 1 milliard d’années-lumière (109 a.l.).
Conclusions
Du fait de l’évolution possible des sources observées, on ne peut pas tester directement l’homogénéité. Par contre on peut vérifier l’hypothèse d’isotropie spatiale de façon directe, sans supposer implicitement l’homogénéité. Le principe de Copernic permet alors de conclure à l’homogénéité. Le relevé de quasars SDSS permet d’étendre cette conclusion jusqu’à une distance de 20 milliards d’années-lumière, correspondant à un décalage vers le rouge (voir Figure 5), z=2.8.
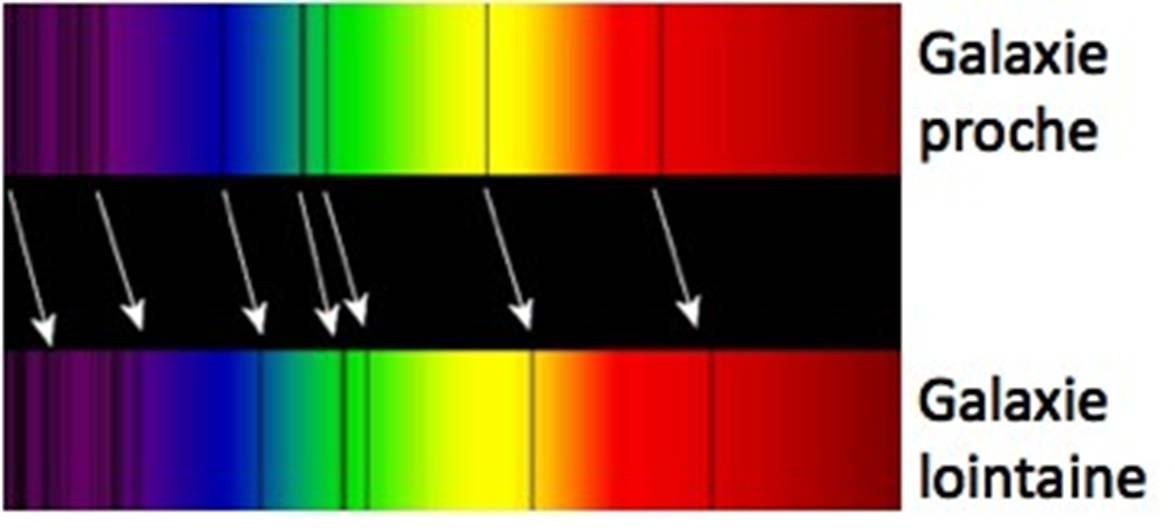
Figure 5: Lorsque qu’une galaxie s’éloigne de nous, les raies de son spectre sont décalées vers les grandes longueurs d’onde, c’est-à-dire vers la partie du spectre correspondant au rouge. Ce décalage va permettre de mesure la vitesse d’éloignement. Combiné à l’autre observation de position, l’âge de la source peut être déduit.
[1] La métrique de Friedmann-Lemaître-Robertson-Walker (FLRW) permet de décrire un espace-temps de géométrie homogène et isotrope. En cosmologie, cette métrique est utilisée pour la description de l'évolution de l'univers aux grandes échelles. Elle constitue l'outil principal amenant la construction du modèle cosmologique standard.
Journal of Cosmology and Astroparticle Physics, Volume 2016, November 2016 ou de façon équivalente http://arxiv.org/abs/1602.09010
Contact: Jean-Marc Le Goff
