Une équipe internationale composée de l'Institut de Radioprotection et de Sûreté Nucléaire (IRSN), du Los Alamos National Laboratory (LANL, USA) et du CEA a mis en évidence, pour la première fois, le phénomène dit de « clustering neutronique », à l'aide d'une expérience de physique des réacteurs ayant eu lieu en 2017 auprès du Reactor Critical Facility (RCF) du Rensselaer Polytechnic Institute (RPI, USA). Cette découverte a un impact direct sur la sûreté nucléaire et sur la capacité à concevoir des simulations neutroniques de haute définition. Les résultats ont été publiés le 1er juillet 2021 dans la revue Nature Communications Physics [1].
Zoom sur ce singulier phénomène, à l'intersection entre théorie des jeux et physique des réacteurs nucléaires !
Un effet de la théorie des jeux, la « ruine du joueur »
Dans une lettre adressée à Pierre Fermat en 1656, Blaise Pascal expliquait les rudiments d'un effet célèbre de la théorie des jeux, connu aujourd'hui sous le nom de « ruine du joueur ».
L'idée est simple : si un joueur, disposant d'une certaine somme initiale d'argent, joue à répétition une mise fixe lors d'un jeu de pile ou face (en perdant ou en gagnant ladite mise au gré de ses pronostics) alors ce joueur finira très certainement ruiné au bout d'un temps plus ou moins long. En effet les fluctuations de la somme à disposition du joueur grandissent au gré des mises et finissent ainsi inexorablement par provoquer une faillite au-delà de laquelle, par définition, le parieur ne peut plus poursuivre son jeu. Pour bien se figurer ce que cette idée a de choquant, et pour définir simplement la théorie du clustering, il faut imaginer ce dernier comme une sorte de prolongation spatiale de la théorie de Pascal et visualiser un très grand nombre de ces joueurs en ligne les uns à côté des autres, réalisant simultanément leurs mises successives en partant tous d'une somme identique. Plus le temps passe, plus la fraction de joueurs ruinés augmente, dépeuplant progressivement de larges zones de l'espace où le siège des perdants est laissé vide. Or, comme le jeu de pile ou face est à somme nulle et que, par conséquent, en moyenne, la somme de départ doit être conservée, il doit exister une fraction de plus en plus faible de joueurs qui, au contraire, s'enrichissent au point de compenser la faillite de tous les autres ! Apparaissent alors, au milieu des sièges vides, des montagnes d'argent accumulé par les gagnants de plus en plus rares et de plus en plus riches...
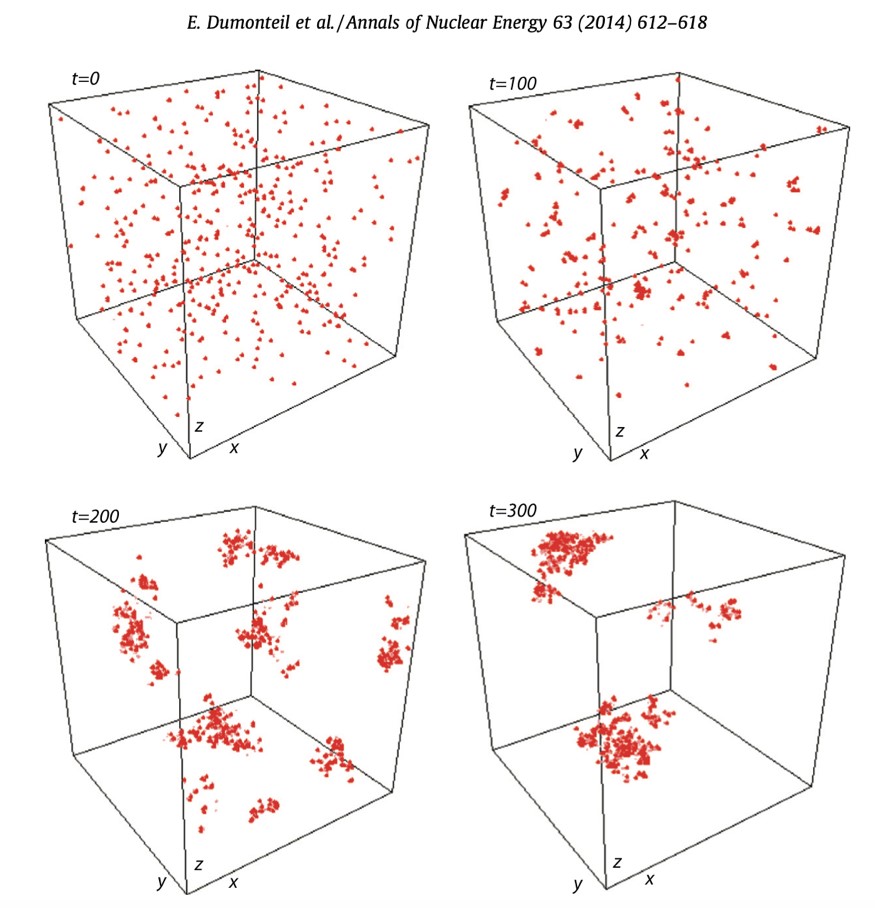
Figure 1. Clustering progressif d'une distribution de neutrons initialement uniforme spatialement. Les neutrons sont simulés par une diffusion branchante binaire (à chaque collision, le neutron a une probabilité 1/2 d'être capturé et une probabilité 1/2 de faire une fission produisant 2 autres neutrons). Après un certain temps, tous les neutrons sont concentrés dans de petites zones de l’espace. Les unités de l'échelle de temps sont arbitraires.
Le clustering neutronique
C'est une version tri-dimensionnelle de cet effet, où l'argent est remplacé par des neutrons : lors de leur transport dans des milieux multiplicatifs, ces derniers induisent des fissions, ou sont capturés. Ainsi, un neutron peut, à chaque collision avec un noyau, soit produire un « gain » d’un neutron supplémentaire par fission, soit produire une « perte » en étant capturé. Comme représenté sur la figure 1, une distribution initiale uniforme de neutrons se voit alors soumise à des fluctuations croissantes dans le temps : les neutrons se regroupent en amas (ou « clusters ») et, si leur diffusion n'est pas suffisante pour lisser ces fluctuations de leur nombre, laissent des vides partout ailleurs.
La modélisation de ce phénomène se fait mathématiquement à l'aide de la théorie des marches aléatoires branchantes : le transport des neutrons est représenté par de la diffusion avec réorientation aléatoire après chaque collision (mouvement Brownien) et les réactions nucléaires de capture ou de fission neutroniques sont modélisées par des processus de Galton-Watson (dits également « birth-death processes »). Les équations résultantes – fondées sur des intégrales de chemin de type Feynman-Kac – permettent alors de déterminer les fluctuations et les corrélations spatiales caractérisant le clustering.
Campagne de mesures expérimentales à Los Alamos
Suite à la parution d'une série d'articles publiés sur le sujet de 2014 à 2016 [2,3,4,5,6], deux physiciens du CEA ont été invités à présenter ces travaux – alors essentiellement théoriques – au Massuchusetts Institute of Technology (M.I.T.) à Boston, où l'idée de faire une expérience « grandeur nature » à l'aide d'un réacteur nucléaire expérimental avait germé. A l'initiative de l'IRSN, intéressé à comprendre et à caractériser au mieux ces effets de corrélations spatiales des populations de neutrons potentiellement présentes au démarrage des réacteurs nucléaires, un programme expérimental a été conçu et une collaboration avec différentes équipes du LANL a été engagée. Les expériences ont eu lieu en 2017 (Figure 2) et leur analyse, s'appuyant sur une campagne de simulations intensives ainsi que sur un « jumeau numérique » du RCF, a duré trois années. Cette longue durée a été nécessaire car, pour la première fois, une statistique réaliste des neutrons du réacteur a été simulée par un code de neutronique de haute fidélité (voir plus loin la notion de simulation analogue).

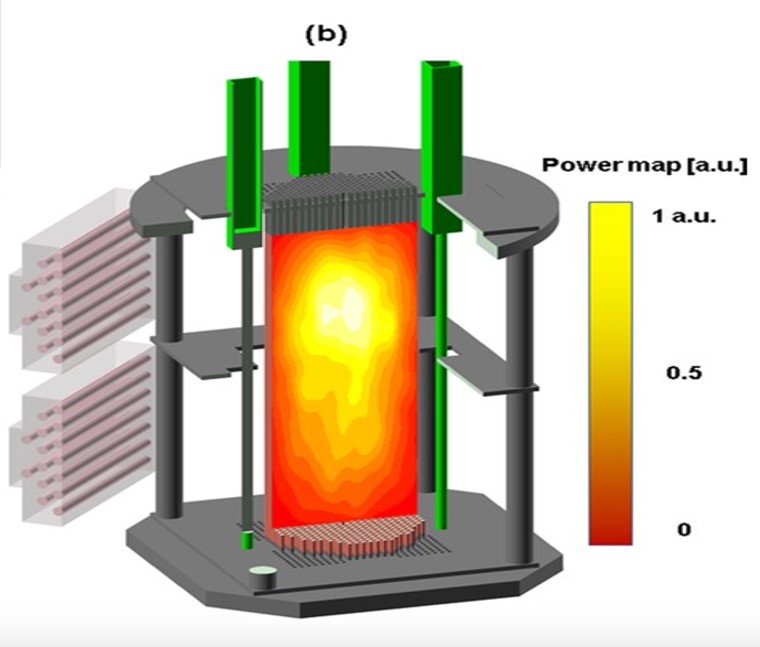
Figure 2. Installation des détecteurs NOMAD auprès du réacteur RCF. L'assemblage contenant les crayons combustibles apparait en bas de l'image (damier d'insertion des crayons). Une fois les détecteurs étanches, la cuve comprenant le réacteur et les détecteurs est immergée sous l'eau. (crédit Los Alamos)
Premiers Résultats
Les expériences ont été menées en partenariat avec Los Alamos National Laboratory, qui a conçu une technologie de détecteurs (dits NOMAD, utilisant des tubes à hélium 3) permettant de réaliser une cartographie unidimensionnelle des neutrons avec de très bonnes résolution en temps. En positionnant deux détecteurs NOMAD l'un sur l'autre, il a alors été possible de réaliser des "instantanés" de la population neutronique couvrant toute la taille du réacteur. Les résultats des expériences ont alors confirmé de manière très nette les prédictions théoriques d'un modèle particulier de clustering neutronique, prenant en compte les sources de fission spontanées du réacteur. Ils soulignent ainsi l'importance de ces dernières pour décrire au mieux les corrélations et les fluctuations au démarrage des cœurs, notamment si ceux-ci sont de grande taille. En effet, on mesure le "clustering" des neutrons à l'aide de la fonction dite "à deux points", notée g(z,t) qui est d'autant plus élevée en son centre que les ceux ci sont regroupés. Or, le modèle de clustering, prenant en compte l'effet des sources de fission spontanées du réacteur, prédit une dépendance des corrélations spatiales proportionnelle à la puissance P du réacteur et une diminution des corrélations linéairement par rapport à la distance caractéristique z sur laquelle celles-ci sont considérées, ce qui a précisément été observé expérimentalement (cf. Figure 3).
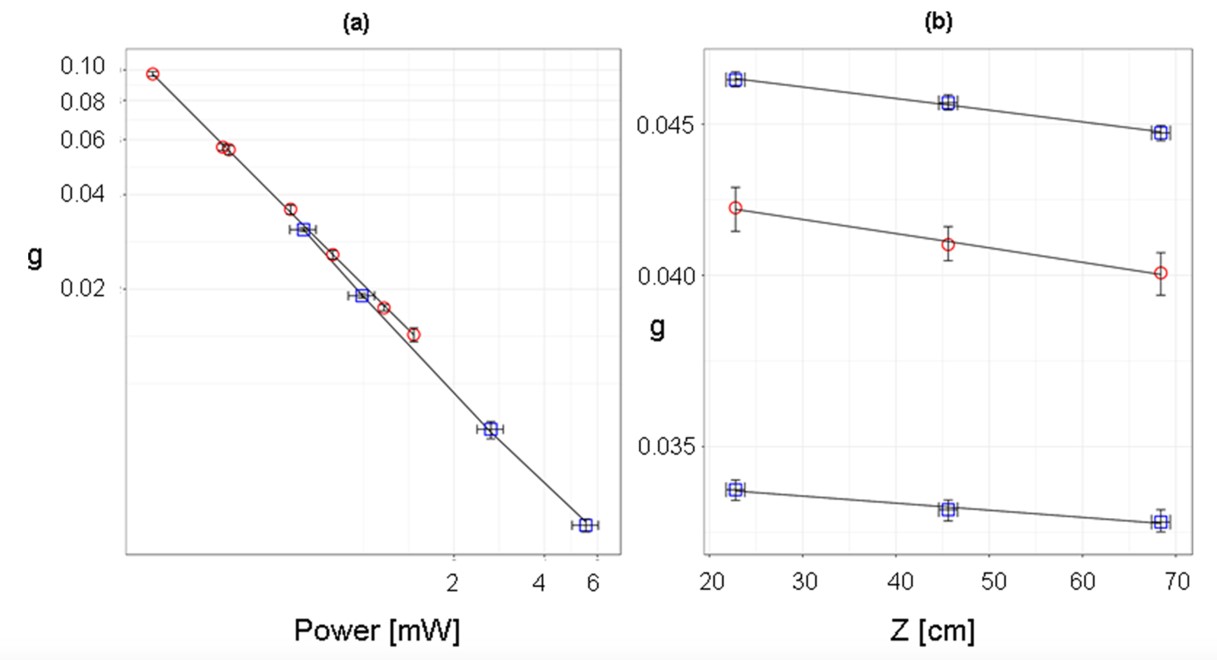
Ces résultats sont également reproduits à l'aide des simulations Monte Carlo du transport des neutrons dites « analogues », c'est à dire au plus proche de la réalité. En effet lors de ces simulations, les fluctuations inhérentes au processus de fission et à l'aléa du nombre de neutrons en voie de sortie de ce processus sont prises en compte. Les résultats numériques ont permis de supporter les conclusions des mesures expérimentales de la Figure 3 et les prédictions théoriques. On voit ainsi sur la Figure 4, (présentant des résultats de simulations calibrées à l'aide des expériences) des effets de clustering très forts lorsque la population de neutrons est « radiographiée » à un instant donné.
Connaitre la répartition des neutrons au démarrage d'un coeur
Cette compréhension affinée du comportement des populations neutroniques à faible puissance et plus généralement de l'émergence de structures spatiales liées à la mécanique statistique des processus branchants, offre une double perspective. Du point de vue de la neutronique, ces travaux sont d'intérêt pour la sûreté nucléaire car ils pourraient à terme contribuer à l'amélioration des démarches de sûreté des phases de « start-up » des cœurs et aider à répondre à des questions d'ingénierie associées à ces phases (utilisation des sources externes de démarrage, apparition de tilts de puissance, etc.). En effet, au démarrage d'un réacteur la puissance étant très faible, le nombre de neutrons l'est également ce qui pourrait induire un effet fort de clustering. Si les neutrons n'explorent pas tout le réacteur, des effets de sur-criticité locaux pourraient rester ipso facto inaperçus et ne se révéler plus brusquement lors de phase de montée en puissance du cœur. Du côté de la physique fondamentale, ces travaux sur les marches aléatoires branchantes ouvrent des perspectives sur la modélisation stochastique et l'utilisation de la simulation Monte-Carlo pour la compréhension de phénomènes diffusifs pour lesquels des théories en champ moyen semblent insuffisantes, comme par exemple l'étude de la phase initiale des épidémies [7] ou la compréhension du phénomène de décohérence en mécanique quantique.
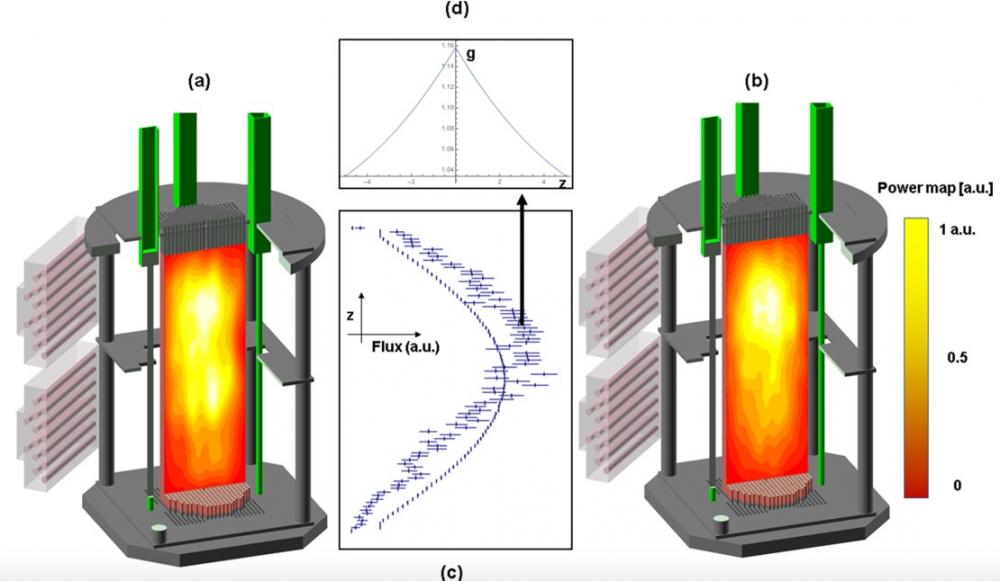
Figure 4. (a) Distribution spatiale de la population neutronique dans le réacteur moyennée dans le temps et où les corrélations spatiales sont ipso facto absentes. (b) Distribution spatiale de la population neutronique dans le réacteur à un instant donné, faisant apparaître un effet fort de clustering des neutrons, majoritairement présents en partie supérieure du réacteur. (c) Les deux distributions spatiales évoquées en (a) et (b) sont projetées sur l'axe Z pour mettre en évidence cet effet de regroupement des neutrons particulièrement prégnant lorsque ceux-ci sont observés avec un "temps d'exposition" court (courbe bruitée avec un clustering neutronique fort en partie supérieur du réacteur), mais très lissé avec des "temps d'exposition" longs (courbe lisse). (d) Ces corrélations spatiales provoquent un pic de la fonction de corrélation g en 0, comme prédit par la théorie.
Contacts: Eric Dumonteil (DRF/Irfu), (DES/ISAS)
[1] E. Dumonteil, E., Bahran, R., Cutler, T. et al., "Patchy nuclear chain reactions.", Commun Phys 4, 151 (2021). https://doi.org/10.1038/s42005-021-00654-9
[2] E. Dumonteil, F. Malvagi, A. Zoia, A. Mazzolo, D. Artusio, C. Dieudonné, C. de Mulatier, " Particle clustering in Monte Carlo criticality simulations.", Ann. Nucl. Energy 63, 612-618 (2014). http://dx.doi.org/10.1016/j.anucene.2013.09.008
[3] A. Zoia, E. Dumonteil, A. Mazzolo, C. de Mulatier, A. Rosso, "Clustering of branching Brownian motions in confined geometries", Phys. Rev. E 90, 042118 (2014). https://doi.org/10.1103/PhysRevE.90.042118
[4] C. de Mulatier, E. Dumonteil, A. Rosso, A. Zoia, " The critical catastrophe revisited.", J. Stat. Mech. P08021 (2015). https://doi.org/10.1088/1742-5468/2015/08/P08021
[5] B. Houchmandzadeh, E. Dumonteil, A. Mazzolo, A. Zoia, "Neutron fluctuations: the importance of being delayed.", Phys. Rev. E 92, 052114 (2015). https://doi.org/10.1103/PhysRevE.92.052114
[6] M. Nowak, J. Miao, E. Dumonteil, B. Forget, A. Onillon, K. Smith, A. Zoia, " Monte Carlo power iteration: Entropy and spatial correlations.", Ann. Nucl. Energy 94 856-868 (2016). https://doi.org/10.1016/j.anucene.2016.05.002
[7] Eric Dumonteil, Satya N. Majumdar, Alberto Rosso, and Andrea Zoia, "Spatial extent of an outbreak in animal epidemics", PNAS 110 (11) 4239-4244 (2013), https://doi.org/10.1073/pnas.1213237110
• Le Département de Physique Nucléaire (DPhN)
• Laboratoire d'études et d'applications des réactions nucléaires (LEARN)