Suite à une série d’expériences réalisées à Jefferson Laboratory (USA) visant à étudier la diffusion élastique électron-proton, il est apparu que les informations sur la structure du proton n’étaient pas cohérentes selon le type d’expérience effectuée. Pour réconcilier ces différents résultats, il a été suggéré qu’un deuxième photon serait échangé pendant l’interaction, au-delà de l’échange d’un photon qui est le mécanisme dominant. L’existence de ce phénomène serait lourde de conséquences, invalidant de nombreuses expériences. La quête d’une preuve expérimentale de l’existence de ce mécanisme a motivé la réalisation de trois expériences, qui ont eu lieu récemment. Nous avons interprété l’ensemble des résultats obtenus et montrons que l’échange de deux photons n’est pas un mécanisme privilégié. D’autres explications, comme un calcul plus précis des corrections radiatives, apparaissent favorisées. Cette étude, menée par deux chercheurs de l’Irfu et de JINR Dubna (Russie), vient d’être publiée dans la revue Physical Review C [1].
La diffusion élastique électron-proton est une réaction dans laquelle l’état initial et l’état final sont identiques, à savoir ici un état constitué de l’électron et du proton. Afin d’étudier la diffusion élastique électron-proton, deux méthodes expérimentales sont couramment utilisées :
- La diffusion ‘Rosenbluth’ : mesure du nombre d’électrons diffusés à chaque angle (les distributions angulaires), avec un faisceau d’électrons non polarisés (i.e. le spin1 des électrons, n’a pas d’orientation privilégiée), pour des angles et énergies différents mais avec la même valeur d’impulsion transférée au proton (q),
- La méthode de ‘Akhiezer-Rekalo’ : mesure de la polarisation du proton de recul (proton dans l’état final), en utilisant un faisceau d’électrons eux-mêmes polarisés.
L’hypothèse sous-jacente aux deux méthodes est que l’interaction advienne à travers l’échange d’un photon virtuel (γ*), c’est-à-dire un photon dont la masse coïncide avec le quadri-vecteur de l’impulsion transférée (Q² = -q²) (Figure 1). Ces expériences permettent d’extraire les ‘facteurs de forme électrique et magnétique’ qui encodent la distribution spatiale de charge électrique et magnétique dans le proton.
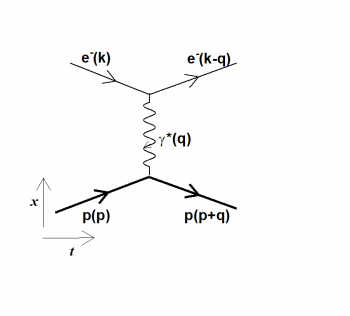
Figure 1 : Diagramme de Feynman représentant la diffusion élastique électron (e-)-proton (p). La réaction a lieu dans le temps (axe horizontal) et dans l’espace (axe vertical). Le proton reste intact, après avoir reçu, et partagé parmi ses constituants, une impulsion (q) par l’après absorption d’un photon virtuel (?*) émis par l’électron incident.
Les mesures ‘Rosenbluth’ donnent des facteurs de forme électrique et magnétique compatibles avec, d’une part, le comportement à grand Q² (impulsion transférée) prédit par la chromodynamique quantique, qui est la théorie de l’interaction forte, et d’autre part, une densité de charge du proton de forme exponentielle, prédite par des modèles semi-classiques. A.I. Akhiezer et M.P. Rekalo ont suggéré dans les années ‘70 une autre méthode, qui n’a pu être appliquée que récemment, suite à la mise en service d’accélérateurs d’électrons de haute intensité fournissant des faisceaux polarisés, ainsi qu’à la conception de nouveaux détecteurs permettant de mesurer la polarisation des protons de recul de haute énergie. Il apparaît que le rapport des facteurs de forme électrique et magnétique extrait grâce à cette dernière méthode est plus précis, mais en désaccord avec celui obtenu par la méthode ‘Rosenbluth’. Ce qui signifie que les distributions de charge électrique et magnétique à l’intérieur du proton sont différentes, contrairement à ce qui était admis auparavant. Cette différence est attribuée au facteur de forme électrique, car la précision sur le terme magnétique par les mesures ‘Rosenbluth’ est bonne (de l’ordre du pourcent).
Echange d'un deuxième photon ?
Pour réconcilier ces deux résultats il a été suggéré que l’échange d’un deuxième photon devait avoir lieu pendant l’interaction. Des recherches expérimentales et théoriques sur les effets de l’interaction à deux photons ont été entreprises dès les années ‘70, mais aucune preuve expérimentale claire n’existe à l’heure actuelle. Dans le cas de l’interaction à deux photons, l’extraction de l’information concernant la structure du proton, en termes de facteurs de forme, est plus compliquée et dépend des modèles sous-jacents. En effet, les calculs de l’échange de deux photons impliquent des hypothèses qui sont peu contraintes par les données. Mais nous pouvons - de façon indépendante des modèles - prédire certaines conséquences de la présence des deux photons lors de l’interaction, et notamment celle-ci : la section efficace de diffusion élastique d’électron sur proton (e-p) doit être différente de la section efficace de diffusion élastique de positron (l’antiparticule de l’électron) sur proton (e+p) [2]. Ceci vient du fait que, dans le mécanisme d’interaction à deux photons, de nouvelles contributions sensibles à la charge du faisceau (électrons ou positrons) apparaissent. Le rapport des sections efficaces de diffusion élastique (e+p/e-p) dans les mêmes conditions cinématiques ne serait plus égal à un.
Trois expériences : VEPP, OLYMPUS et CLAS
Même si l’émission d’un photon supplémentaire est cent fois moins probable (l’émission de chaque photon est accompagnée d’un facteur α, la constante de structure fine de l’interaction électromagnétique, σ ~ 1/137), des modèles ont prédit une probabilité relative de l’émission des deux photons jusqu’à 10%. Trois expériences se sont évertuées à mesurer le rapport des sections efficaces de diffusion élastique (e+p/e-p) avec un faisceau d’électrons et de positrons : VEPP à Novosibirsk (Russie) [3], OLYMPUS à DESY (Allemagne) [4], CLAS à Jefferson Laboratory (USA) [5]. Les techniques et les erreurs associées étant très différentes, les résultats de ces expériences, publiés en 2015 et 2017, sont à considérer comme des mesures indépendantes.
En 2010, nous avions déjà déterminé une limite supérieure de la contribution de l’interaction à deux photons dans la diffusion élastique électron-proton [6], en calculant celle dans la diffusion élastique électron-muon (le muon est une particule élémentaire de la même famille que l’électron mais environ 200 fois plus massive).
Plus récemment, en 2014, nous avons montré l’importance de considérer les corrections radiatives lors de l’étude de la diffusion élastique électron-proton [7]. Ces corrections consistent à prendre en compte précisément les pertes d’énergie des particules chargées par émission de photons. Ce rayonnement électromagnétique peut modifier la cinématique des particules avant ou après le point d’interaction. Par un calcul de corrections radiatives, nous avons montré que le plus grand écart entre la section efficace de diffusion élastique (e+p) et (e-p), c’est-à-dire l’asymétrie de charge, est dû à l’interférence des photons émis par l’électron (initial et final) [8].
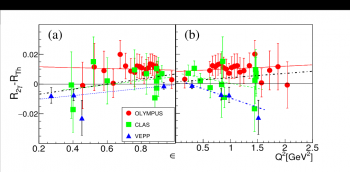
Figure 2 : Différence entre le rapport R, représentatif de l’asymétrie de charge, théorique (RTh) et expérimental (R2?) pour les données les trois expériences VEPP (triangles bleus), OLYMPUS (cercles rouges) et CLAS (carrés verts). Ce rapport est tracé en fonction d'une variable epsilon représentative de l’angle de diffusion, et du Q², l’impulsion transférée pendant l’interaction. Une déviation par rapport à zéro serait la preuve d’une forte contribution de l’échange des deux photons. Figure extraite de la référence [1].
Suite aux trois expériences récentes, nous avons réinterprété l’ensemble des résultats par rapport à notre calcul d’asymétrie de charge [1]. La Figure 2 montre la différence entre notre calcul et les données des trois expériences récentes, du rapport des sections efficaces de diffusion élastique positron-proton (e+p) sur électron-proton (e-p), après correction radiatives. Cette différence est compatible avec zéro pour la majorité des points, qui sont à l’intérieur d’un intervalle de ±0,02. L’analyse des données est donc en accord avec notre modèle, et aucune déviation au-delà de 2% n’a été mise en évidence. Ce ‘quelques pourcents’ est l’ordre de grandeur de l’incertitude sur les corrections radiatives au premier ordre en α, ainsi que sur les résultats expérimentaux. De plus, les données ne montrent pas de corrélation marquée avec les variables cinématiques choisies (ε, variable liée à l’angle de diffusion, et Q², l’impulsion transférée). C’est cette même corrélation qui avait donné lieu à diverses hypothèses et notamment celle d’une possible interaction à deux photons. Ces résultats ont été publiés dans Physical Review C, en accès libre après sélection par SCOAP3 [1].
A la lumière de notre travail, il semble très improbable que l’échange des deux photons soit la cause du désaccord entre les mesures polarisées et non-polarisées des facteurs de forme. L’impact possible des corrections radiatives sur ce désaccord avait déjà été soulevé par notre équipe [7], ainsi que par des chercheurs de Novosibirk [9], il y a quelques années. Nos récents travaux vont en faveur d’explications alternatives, telles que la prise en compte de corrections radiatives précises, plutôt qu’en l’existence d’un mécanisme tel que l’émission de deux photons lors de l’interaction. Cela remet de l’ordre dans les données existantes et confirme l’importance de la précision dans les mesures des facteurs de forme obtenue par les techniques de polarisation.
1. Le spin est une quantité purement quantique, qu’on assimile à la direction dans laquelle les particules tournent autour d’elles-mêmes. Pour un électron (ou un proton), le spin ne peut avoir que deux valeurs : +1/2 ou -1/2. Dans une direction verticale l’électron (ou le proton) est alors orienté (polarisé) vers le haut ou vers le bas.
Références :
[1] V. V. Bytev, and E. Tomasi-Gustafsson, Phys. Rev. C99, 025205 (2019).
[2] M. P. Rekalo and E. Tomasi-Gustafsson, Eur. Phys. J. A22, 331 (2004).
[3] I. A. Rachek, et al., Phys. Rev. Lett. 114, 062005 (2015).
[4] B. S. Henderson et al., (OLYMPUS Collaboration), Phys. Rev. Lett. 118, 092501 (2017).
[5] D. Rimal et al., (CLAS Collaboration), Phys. Rev. C 95, 065201 (2017).
[6] E. A. Kuraev and E. Tomasi-Gustafsson, Phys. Part. Nucl. Lett. 7, 67 (2010).
[7] E. A. Kuraev, Yu. M. Bystriskiy, A. I. Ahmadov and E. Tomasi-Gustafsson , Phys. Rev. C89, 065207 (2014).
[8] E. A. Kuraev, V. V. Bytev, S. Bakmaev and E. Tomasi-Gustafsson, Phys.Rev. C78, 015205 (2008).
[9] A. V. Gramolin, et al., J. Phys. G41, 115001 (2014).
Contact : Egle Tomasi-Gustafsson (IRFU/DPhN)
• Structure de la matière nucléaire › Structure en quarks et gluons des hadrons



